Історія математики у Вірменії

Матеріал з testwiki
Перейти до навігації Перейти до пошуку

Історія математики у Вірменії бере початок ще з часів Урартського царства (IX—VII ст. до н. е.), коли використовувалися десяткова і шістдесяткова системи числення, і роль цифр виконував клинопис. Порівняння арифметики в стародавній Вірменії з урартською вказує на їх безпосередній зв'язок. Сліди урартської арифметики помітні в стародавній Вірменії ще в епоху, коли жив і працював Ананія Ширакаці, і в арифметиці, що використовувалася пізніше.

Вже після створення вірменського письма в V столітті в системі числення в якості цифр використовувалися вірменські літери. Одним з перших вірменських вчених в галузі математики вважається найбільший учений VII століття Ананія Ширакаці. Він був автором відомого підручника арифметики. Також відомі середньовічні математики Шаблон:Нп, Шаблон:Нп, Ованес Імастасер, Григор МагістросШаблон:Перехід.

В період XVII—XIX століть у вірменських колоніях відкрилися вірменські школи, в яких велося викладання математики. У цей період активно видавалися математичні книги вірменською мовою. В цілому в період XVII—XIX століть було видано близько 90 підручників і посібників вірменських авторівШаблон:Перехід.

У XX столітті в Єревані були засновані Єреванський державний університет (1921), Єреванський політехнічний інститут (1931, нині — Національний політехнічний університет Вірменії), Єреванський педагогічний інститут (1922, нині — Вірменський державний педагогічний університет імені Хачатура Абовяна), Академія наук Вірменської РСР (1943, нині — Національна академія наук Республіки Вірменія, у 1944 році засновано Інститут математики), де ведуться фундаментальні дослідження з теорії наближень, теорії функцій, функціональному аналізу, інтегрального і диференціального числення й інших галузей математикиШаблон:Перехід.

Давнина і Середньовіччя

Урарту

Найдавніші джерела про математичні знання на території Вірменії — це клинописні таблички часів Урартського царства (IX—VII століття до н. е.). Вони свідчать, що у той час використовувалися десяткова і шістдесяткова системи численняШаблон:Sfn. Десяткова система докорінно відрізнялася від єгипетської і була близька до сучасної системиШаблон:Sfn. Клинописні таблички також свідчать, що за допомогою декількох символів записувалися досить великі цілі числа, а також дробові числа, і з ними проводилися операції додавання та відніманняШаблон:Sfn. Нижче наводиться кілька прикладів чисел, взятих з царських написів Сардурі II, де одиниці — , десятки — , сотні — , тисячі — Шаблон:Sfn:

Урартійці, високо оцінюючи ассиро-вавилонську культуру, переймають у них клиноподібні письмена, створюють свою писемність і літературу, використанням клиноподібних цифр вводять у вжиток і роблять ужитковими великі числаШаблон:Sfn. Порівняння арифметики в стародавній Вірменії з урартською вказує на їх безпосередній зв'язокШаблон:Sfn.

Створення вірменського алфавіту

Про математичних знаннях вірмен, особливо в V—VI століттях можна скласти уявлення з одного боку судячи за філософськими та історичними працям, де досліджуються деякі проблеми математики та астрономії, а з іншого боку — за залишками речової культури (замки, палати, церкви, мости і зрошувальні системи), для будівництва яких були потрібні математичні знання і точні розрахунки, а також за участю вірмен у міжнародній торгівлі. В V і на початку VI століть велика кількість спеціально відібраних учнів з Вірменії були відправлені для продовження навчання в Олександрію, Афіни і Рим. Про це свідчили вірменські історики V століттяШаблон:Sfn.

До нинішніх часів вченим — історикам науки не вдалося знайти чисто математичних текстів, створених вірменами до V століття, коли Месропом Маштоцем було створено вірменський алфавітШаблон:Sfn. Після створення вірменського алфавіту відкрилися вірменські школиШаблон:Sfn, де викладали також і математику. Вірменські букви використовувалися в якості цифр, була створена алфавітна десяткова не позиційна система числення, яка наведена нижче (наприклад: Գ — 3, Խ — 40, Չ — 700, Ք — 9000). Між алфавітними системами вірмен і греків, поряд зі схожістю, існувало і деяке розходження. Вірмени вживали 36 букв, а греки — 27. Урартська система використовувалася паралельно з алфавітною, до тих пір, поки не була остаточно витіснена нею. Але сліди урартської системи залишилися в новій і передавалися з покоління в поколінняШаблон:Sfn.

Ананія Ширакаці

Статуя Ананії Ширакаці перед будівлею Матенадарану в Єревані
Сторінка з підручника арифметики Ананії Ширакаці, 1283 рік

Древні математичні праці вірменською мовою, що дійшли до нас, пов'язані з ім'ям великого вірменського науковця VII століття, основоположника давньовірменського природознавства Ананії Ширакаці. Те, що до Ананії Ширакаці в V—VI століттях існували вірменські математики та математичні праці вірменською мовою, очевидно з одного свідчення Ширакаці. У вступі до таблиць додавання Ананія Ширакаці згадав, що він переписує в стислому вигляді праці своїх предків: Шаблон:Цитата Ананія Ширакаці зробив значний внесок у математику. Ним був складений підручник арифметики, що має декілька частин: таблиці з операціями додавання і віднімання, таблиці з операціями множення та ділення, таблиці чисел виду 6000n, де n пробігає всі значення букв вірменського алфавіту, а частки округлюються до цілого числа (Шеститисячник, Шаблон:Lang-hy). У Вірменії також були аналогічні таблиці для чисел виду 5000n,4000n та деяких іншихШаблон:Sfn. Задачник складений Ананією Ширакаці складається із 24 завдань з відповідями та із завдань з цікавим змістом (Шаблон:Lang-hy). Майже у всіх завданнях з задачника Ананії Ширакаці відображено життя вірменського народу: або в умовах йдеться про події вірменської історії, або застосовуються вірменські міриШаблон:Sfn. Завдання — лінійні, з одним невідомим, в одному (№ 22) потрібно поділити величину в арифметичній прогресії. Дроби, що зустрічаються в завданнях, записані у вигляді сум частин одиниціШаблон:Sfn.

На початку VII століття у Візантії, державною релігією якої було християнство, починається серйозна боротьба проти язичницької науки і її представників. У зв'язку з цими подіями, значення природничих наук і математики у Вірменії сильно падає. Про це пише Ананія Ширакаці в автобіографіїШаблон:SfnШаблон:Sfn.

Істориками науки показано, що починаючи з I століття до н. е. у Вірменії застосовували такі міри довжиниШаблон:Sfn: аспарез (по повітрю), рівний 10717 крокам, аспарез (по землі) — 14267 і 150 крокам, градус, що містить в собі 500 аспарезів. Миля становила 7 аспарезов і в одному випадку дорівнювала 1000 кроків, в іншому — 1050, а крок — 6 стопам, стопа — 16 пальцям. У VII столітті у Вірменії відстань між двома містами міряли милями, а відстань між планетою і Землею — аспарезамиШаблон:Sfn. Вся інформація про міри довжини була наведена у праці Ананія Ширакаці «Ашхарацуйц» (Шаблон:Lang-hy)Шаблон:Sfn.

Математика у Вірменії після VII століття

Григор Магістрос

Продовжувачем традицій Ширакаці є відомий візантійський математик і механік вірменського походження Шаблон:Нп (бл. 790 — бл. 869). У Константинополі він займався викладанням математики, а у 863 році створив і став першим ректором Константинопольського університету. В математиці Лев систематично застосовував літери як арифметичні символи, передбачаючи становлення алгебри; він значно спростив складну символіку Діофанта і зробив подальший крок у розвитку алгебричного напрямку в математиціШаблон:Sfn. Значний внесок в галузі математичної освіти кінця XI початку XII століття має Ованес Імастасер (Любомудрий), відомий також як Іоанн Саркаваг (1045/55—1129). З його математичних праць видно, що у вірменських середньовічних школах окрім практичної вивчали також теоретичну арифметику — теорію чисел. Одна з його праць включає вірменську версію таблиць множення Піфагора. Його твір «Багатокутні числа» спирався на «Арифметику» НікомахаШаблон:Sfn. Ованес Імастасер є автором праці «Полігональні числа», яка використовувалася в якості підручника у XI—XII століттяхШаблон:Sfn.

Математична освіта у Вірменії досягла високого рівня у XI—XIV століттях у вірменських середньовічних університетах: у Гладзорському університеті (заснований у 1282 році), в Татевському університеті (заснований у 1373 році), також у школах Ані, Ахпата і в інших навчальних закладах, зокрема й за межами ВірменіїШаблон:Sfn.

Також продовжувачем традицій Ширакаці є візантійський математик вірменського походження XIV століття Шаблон:НпШаблон:Sfn. Збереглися його два листи грецькою мовою. В одному з них йдеться про те, як можна подати пальцями руки числа від 1 до 9999, а в іншому — про добування квадратного кореня з чиселШаблон:Sfn.

У вірменських школах використовувалися праці грецьких класиків. Вірменські вчені займалися перекладами цих праць. «Начала» Евкліда були перекладені вірменською мовою кількома авторами. Окремі частини перекладу, що збереглися, відносяться і до Ананії Ширакаці, і до Григора Магістроса (переклав безпосередньо з грецького тексту в 1051 році)Шаблон:SfnШаблон:Sfn, і до інших. Згідно з Шаблон:Нп, найстарішим, після арабського, перекладом «Начал» Евкліда є вірменський переклад Григора Магістроса. Фрагменти «Начал» Евкліда у вірменському перекладі, що дійшли до нас, містять переліки постулатів і аксіом, що були покладені в основу «Начал»; вони проливають нове світло зокрема на постулат про паралельніШаблон:SfnШаблон:Sfn. У 1959 році було виявлено ще один переклад «Начал», зроблений Шаблон:Нпні в XVII століттіШаблон:Sfn.

XVII—XIX століття. Вірменська математична література

У XVII—XVIII століттях питаннями математичної науки також займалися історики-філософи. Великі частини їхніх виданих праць були присвячені проблемам арифметики і геометріїШаблон:Sfn. В даний період було видано багато книг, важливих для математики і математичної освіти.

Перша Шаблон:Нп математична книга вірменською мовою «Мистецтво числення» обсягом 147 сторінок була видана в Марселі в 1675 році. Автор невідомий. У вступі до цієї книги він вказав, що він написав книгу для торговців, оскільки вони були неграмотними в математиціШаблон:Sfn. Автор не використовував знаки додавання, віднімання, множення, ділення, рівності, хоча відповідні поняття в книзі постійно використовувалися. В даній праці були використані французькі, італійські, іранські математичні терміниШаблон:Sfn. В подальшому було виявлено, що «Мистецтво числення» є перекладом праці Христофора Клавія з латинської мовиШаблон:Sfn. У XVII столітті також без зазначення імені автора та точного часу видання була видана книга обсягом 120 сторінок, 109 з яких — арифметичні таблиці: таблиця квадратів чисел 1-100, таблиця множення чисел 1-100 на 2, таблиця множення чисел 1-100 на 3 (і так далі до 100), таблиця множення чисел 1-100 на 200, таблиця множення чисел 1-100 на 300 (і так далі до 1000)Шаблон:Sfn. У 1781 році у Венеції була видана книга Сукиаса Агмалянца «Арифметика» обсягом 511 сторінокШаблон:Sfn. Книга присвячена додаванню, відніманню, множенню, діленню, порівнянню, арифметичним і геометричним прогресіям і логарифмамШаблон:Sfn. У 1794 році також у Венеції було видано книгу Саака Проняна «Геометрія» об'ємом 423 сторінкиШаблон:Sfn. Книга присвячена геометричним теоремам і аксіомам і дослідженню геометричних термінів (лінії, кути, трикутники, кола тощо)Шаблон:Sfn. Вже після смерті Саака Проняна, в 1810 році у Венеції видається його «Тригонометрія». У цій книзі вперше в історії вірменської математичної літератури використовуються математичні знакиШаблон:Sfn. Книга присвячена тригонометрії, розв'язуванню трикутників, сферичній геометрії.

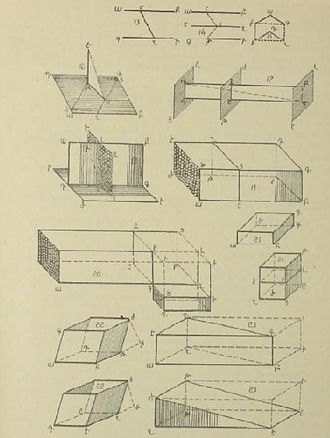
Сторінки з вірменських математичних книг
Титульна сторінка першої друкованої математичної книги вірменською мовою «Мистецтво числення». 1675 рік, Марсель Креслення з вірменської редакції XVII століття «Начал» Евкліда

У вірменській математичній літературі XVII—XVIII століть у багатьох випадках використовуються російські терміни. Написані в Астрахані в 1744 1753 і в 1807 роках вірменські рукописи, присвячені обчислювальному мистецтву, містять арифметичні задачі, в яких вживаються терміни «карбованець», «копійка» та інші, а також російські назви цифрШаблон:Sfn. У російські навчальні заклади Астрахані, в яких викладали багато предметів, зокрема геометрію, потрапляли і закінчували їх лише окремі представники вірменського населення, кількість яких ніяк не могла задовольнити фактичні потреби в освітіШаблон:Sfn. 12 грудня 1810 року відкривається Агабабівська школа в Астрахані, де більша частина вірменського населення мала можливість отримати освітуШаблон:Sfn. В 1828 році, коли Східна Вірменія увійшла до складу Російської імперії, почали відкриватися вірменські навчальні закладиШаблон:Sfn. 9 грудня 1838 року в Константинополі відкривається Скютарська семінаріяШаблон:Sfn, викладачі якої були вірменами, що отримали європейську освіту.

Велике значення мають праці Гукаса Тертерянца, видані у Відні. У 1843 році видаються відразу два підручники: «Арифметика» і «Проста Геометрія». У 1846 році видається книга «Тригонометрія та конічні перерізи», об'ємом 134 сторінкиШаблон:Sfn. Друга частина книги присвячена аналітичній геометрії. В кінці книги подано 34 геометричні креслення.

В цілому в період XVII—XIX століть було видано близько 90 підручників і посібників вірменських авторівШаблон:Sfn.

XX—XXI століття

XX століття

У 1921 році в Єревані було засновано вірменський університетШаблон:Sfn. Викладання вищої математики почали з дня заснування університету на технічному факультеті і факультеті природознавства, а математиків готували, починаючи з 1924 року, на фізико-математичному відділі педагогічного факультетуШаблон:Sfn. Але в період 1921—1933 років в університеті готували тільки вчителів математики для загальноосвітніх і середніх професійних шкілШаблон:Sfn. Вже після 1933 року фізико-математичний факультет Єреванського державного університету став дійсно університетським факультетом з 5-річним навчальним планом, там стали готувати вчених-математиківШаблон:Sfn. У 1959 році фізико-математичний факультет був розділений на механіко-математичний і фізичний факультети. З 1963 року на факультеті почали готувати вчених у галузі математичної кібернетики, а в 1972 році був створений факультет прикладної математики та інформатики[1].

Самостійна науково-творча діяльність у галузі математики в Радянській Вірменії почалася у 1937—1941 роках, коли кілька випускників фізико-математичного факультету Єреванського державного університету продовжили навчання в Москві і в Ленінграді, захистили дисертації і повернулися в ЄреванШаблон:Sfn.

Будівля Президії Національної академії наук Республіки Вірменія Будівля Єреванського державного університету Будівля Національного політехнічного університету Вірменії

У 1943 році було засновано Академію наук Вірменської РСР (на основі Вірменської філії Академії наук СРСР, створеної в 1935 році, нині — Національна академія наук Республіки Вірменія)[2]. В 1944 році було створено відділення механіки і математики АН Вірменської РСР. Пізніше відділення було перетворено на Інститут математики і механіки АН Вірменської РСР}}. Інститут математики був виділений в окрему організацію в 1971 році. У 1956 році був створений Єреванський науково-дослідний інститут математичних машин (нині — Єреванський науково-дослідний інститут автоматизованих систем управління). У 1957 році був створений Обчислювальний центр АН Вірменської РСР (нині — Шаблон:Нп), де почали досліджувати математичні проблеми кібернетики та обчислювальної техніки, математичну забезпеченість систем автоматизації, автоматизацію наукових досліджень. Великим центром досліджень в галузі прикладної математики, інформатики і комп'ютерних систем також є Національний політехнічний університет Вірменії. У 1961 році в НПУВ було створено факультет комп'ютерних систем та інформатики. Також в університеті є факультети прикладної математики і фізики, кібернетики[3].

Поштова марка Вірменії, присвячена Шаблон:Нп

Біля витоків створення вірменської математичної школи стояв академік АН Вірменської РСР Шаблон:Нп (1906—1978)Шаблон:Sfn. Арташес Шагінян був першим радянським вірменським математикомШаблон:Sfn. Після закінчення аспірантури Ленінградського університету в 1937 році він повернувся в Єреван, успішно займався одночасно науковою і педагогічною роботоюШаблон:Sfn. Послідовниками вірменської математичної школи стали: М. М. Джрбашян, С. М. Мергелян, Шаблон:Нп, Н. Х. Арутюнян, Шаблон:Нп, Шаблон:Нп, Н. Г. ГаспарянШаблон:Sfn, Г. В. БадалянШаблон:Sfn, Н. Є. Товмасян, А. А. Талалян, В. А. Мартиросян, Шаблон:Нп, Шаблон:Нп; сучасні вчені Шаблон:Нп, А. Б. Нерсісян, Шаблон:Нп, Шаблон:Нп, Шаблон:Нпні, Шаблон:Нпні та багато інших[4].

Теорія наближень

Дослідження питань про повноту поліномів у комплексній області у Вірменії були розпочаті в кінці 1930-х років Арташесом ШагіняномШаблон:Sfn і активно продовжувались у 1940-х роках академіками АН Вірменської РСР Мхітаром Джрбашяном (1918—1994) і Сергієм Мергеляном (1928—2008)Шаблон:SfnШаблон:Sfn. Була досліджена можливість наближення функцій поліномами, а також питання про найкраще наближення, щодо інтегральної та рівномірно-вагової метрикШаблон:Sfn. У разі інтегральних метрик були отримані точні ознаки для деяких широких класів областей. Було отримано повний розв'язок рівномірно-вагового поліномного наближення для дійсної осіШаблон:Sfn. Так з половини 1940 рр. почалася організація вірменської математичної школи теорії функційШаблон:Sfn.

Сергієм Мергеляном було отримано розв'язок для рівномірного наближення поліномами в комплексній областіШаблон:Sfn. Цей метод був успішно застосований також у питаннях про можливості рівномірного наближення раціональними функціями, про найкраще поліномне наближенняШаблон:Sfn. Ці роботи Сергія Мергеляна було відзначено Сталінською премією.

У 1950-х роках Мхітаром Джрбашяном були розпочаті дослідження середнього, рівномірного і дотичного наближень цілими функціями, які отримали остаточний розв'язок у 1960-1970-х рокахШаблон:Sfn. Повністю були розв'язані задачі про рівномірне наближення аналітичними (частково цілими) функціями, задача про опис швидкості дотичного наближенняШаблон:Sfn.

Академіком АН Вірменської РСР Норайром Аракеляном були отримані розв'язки кількох загальних задач про найкращі наближення цілими функціями. Ці роботи Норайра Аракеляна були відзначені премією Ленінського комсомолуШаблон:Sfn. Ці результати були успішно застосовані в теорії розподілу значеньШаблон:Sfn. Починаючи з 1970-х років, Мхітаром Джрбашяном та іншими були здійснені дослідження повноти і базисності деяких систем аналітичних функційШаблон:Sfn. Норайром Аракеляном були отримані цінні результати про взаємозв'язок питань про класичне аналітичне продовження і теорію комплексного наближенняШаблон:Sfn.

Загальна теорія функцій

Серйозні дослідження в галузі теорії функцій у Вірменії почалися в 1945 році, коли Мхітаром Джрбашяном була побудована теорія факторизації необмежених мероморфних функцій в областіШаблон:Sfn. У 1950—1960 роках Мхітаром Джрбашяном досліджувалися питання гармонійного аналізу в комплексній області та теорії інтегральних перетвореньШаблон:Sfn. Джрбашян побудував ідеальну теорію перетворень виду Фур'є — Планшереля для довільної системи променів, що виходять з однієї точки; отримав нові фундаментальні результати в поданні загальних і аналітичних функцій; розширив і розробив відому класичну Шаблон:Нп; разом з учнями розробив теорію дискретного гармонічного аналізу в комплексній областіШаблон:Sfn. У 1963 році Мхітаром Джрбашяном були визначені нові класи мероморфних функцій, пов'язаних з функціями на (−1,+∞), які в змозі включити довільні мероморфні функції в крузі, була розроблена теорія параметричного подання даних функційШаблон:Sfn.

Дослідження в цій галузі провів і Шаблон:Нп Ванік Захарян. Мхітаром Джрбашяном і Ваніком Захаряном були досліджені граничні властивості підкласів мероморфних функцій обмеженого видуШаблон:Sfn.

Питаннями дефектних значень загальних і мероморфних функцій займався Норайр АракелянШаблон:Sfn. Вперше використавши методи в теорії наближень, Норайр Аракелян спростував відому гіпотезу Шаблон:Нп про дефектні значення цілих функцій скінченного порядкуШаблон:Sfn.

В геометричній теорії мероморфних функцій і в теорії розподілу значень нові результати отримав Григорій Барсегян, розробивши теорію Неванлінни — АльфонсаШаблон:Sfn.

У дослідженнях теорії аналітичних функцій важливе місце займають питання про єдиність, зокрема про Шаблон:НпШаблон:Sfn. Розробляючи відомі результати Лоренца Ланделефа, Арташес Шагінян отримав «внутрішні» інтегральні ознаки для аналітичних функцій в крузі, які в подальшому поширив на мероморфні функції в крузіШаблон:Sfn. Деякі з цих результатів Ванік Захарян поширив на класи ДжрбашянаШаблон:Sfn.

Мхитар Джрбашян, ґрунтуючись на своїй теорії гормонального аналізу в комплексній області, узагальнив класичну ідею про квазіаналітичність Данжуа — Карлемана, побудувавши теорію α-квазианалитичных класівШаблон:Sfn.

Важливі дослідження в галузі квазіаналітичних функцій має Гайк БадалянШаблон:Sfn. Він ввів деяке узагальнення поняття похідної і, спираючись на нього, побудував спеціальні ряди, більш загальні, ніж тейлорівськіШаблон:Sfn. Ці ряди виявилися відповідним аналітичним засобом для подання функцій деяких квазіаналітичних класівШаблон:Sfn.

Теорія функцій дійсної змінної

Олександр Андранікович Талалян

Дослідження в галузі функцій дійсної змінної (аналітичних функцій) у Вірменії почалися в 1950-х рокахШаблон:Sfn. У початковому періоді дослідження в основному стосувалися питання про подання вимірних функцій ортогональними (зокрема — тригонометричними) рядами і до питання про одиничність цих рядівШаблон:Sfn. У цій галузі здійснив дослідження академік НАН РВ Олександр Талалян (1928—2016)Шаблон:Sfn. Олександр Талалян довів загальні теореми, згідно з яким рядами повних ортогональних систем можуть бути подані всі вимірні функціїШаблон:Sfn. З 1965 року під керівництвом Олександра Талаляна ведуться дослідження загальних ортогональних систем і базисівШаблон:Sfn. Отримані важливі результати про існування універсальних (у різних сенсах) ортогональних рядівШаблон:Sfn. Розв'язана задача відновлення рядів Уолша, схожих з інтегровними функціями, і доведено такі теореми єдиності типів Кантора і Валле Пуссена для систем Гаара і Уолша, подібні з якими для тригонометричних систем не існували або не були відомі до цьогоШаблон:Sfn.

Деякі дослідження в галузі теорії функцій комплексної змінної здійснив Гайк БадалянШаблон:Sfn. Задача Сеге про покриття відрізків розв'язана Гайком Бадаляном для обмежених функцій з класу SШаблон:Sfn.

Функціональний аналіз

Дослідження в галузі функціонального аналізу почалися в 1950-х роках в Єреванському університеті та в Інституті математики АН Вірменської РСР, і були присвячені питанню про подібність граничних задач нового типу в гільбертовому просторі з задачею КошіШаблон:Sfn. Ці дослідження здійснив академік АН Вірменської РСР Рафаель Александрян (1923—1988)Шаблон:Sfn. За цикл робіт «Математичні дослідження з якісної теорії обертової рідини» він був удостоєний Державної премії СРСР. Надалі кількома вченими була розширена тематика досліджень в галузях функціонального аналізу та інтегрального та диференціального численьШаблон:Sfn. Основними напрямками досліджень були: теорія операторів, операторні рівняння, спектральна теорія самоспряжених операторівШаблон:Sfn. Була розроблена ідея ядра спектру, особливо термін резольвенти довільного самосопряженного оператора, а також універсальний спосіб побудови повної системи власних функціоналів і теореми про спектральний аналізі за даними функціоналамиШаблон:Sfn. Було виявлено асимптотичні періодичні умови розв'язків нестаціонарних операторних рівнянь деяких класів, що містять рівняння ШредінгераШаблон:Sfn.

Вперше на зворотні задачі спектрального аналізу диференціальних операторів і на їх важливість для застосувань звернув увагу Віктор Амбарцумян (йому ж належить такий перший результат у цих задачах: якщо для безперервної функції φ(x) крайова задача y'′+π(x)y+λy=0, де 0⩽x⩽π і y'(0)=y'(π)=0має спектр λn=n2(n=1,2,3,⋯), то φ(x)=0)Шаблон:Sfn. Академік АН СРСР Віктор Амазаспович Амбарцумян (1908—1996) є одним з найбільших астрофізиків XX століття. Важливі також його праці з суміжних з астрофізикою наук: математики і фізики.

Деякі з результатів про спектр диференціального оператора L у просторі L(0,∞) перенесені академіком АН Вірменської РСР, радіофізиком Шаблон:Нп на диференціальні оператори в часткових похіднихШаблон:Sfn.

Інші розділи математики

Дослідження у галузі інтегрального та диференціального числень почалися у Вірменії в 1930-х рокахШаблон:Sfn. У цей період вірменські математики отримали деякі результати про параболічні рівнянняШаблон:Sfn. Узагальнені дослідження велися з 1948 року Рафаелем АлександряномШаблон:Sfn. Основними темами досліджень були еліптичні, гіпоеліптичні, гіперболічні, слабкі гіперболічні, інтегральні (зокрема сингулярні інтегральні) рівнянняШаблон:Sfn. Досліджувалися граничні задачі нового типу для деяких некласичних систем диференціальних рівнянь, для рівняння коливання струни в області Діріхле; було розроблено поняття узагальненої власної функціїШаблон:Sfn. Ішханом Саргсяном досліджено спектральний аналіз задачі Штурма — Ліувілля, отримані результати поширені на однорідні системи ДіракаШаблон:Sfn. Також досліджувалися обернена задача Штурма — Ліувілля і обернена задача теорії розсіяння за наявності рівнянь високого порядкуШаблон:Sfn.

У галузях теорії ймовірностей і математичної статистики дослідження у Вірменії почалися в повоєнний часШаблон:Sfn. Було отримано низку результатів з теорії випадкових процесів, а в подальшому про критерій χ2Шаблон:Sfn.

У 1970—1980 роках роботами академіка АН Вірменської РСР Рубена Амбарцумяна було створено новий науковий напрямок — комбінаторна інтегральна геометріяШаблон:Sfn. Комбінаторна інтегральна геометрія успішно застосовувалася в дослідженні розв'язків задач стохастичної геометрії, зокрема, розв'язані задачі стереології геометричних випадкових процесівШаблон:Sfn. Також досліджувалися інші питання стохастичної геометріїШаблон:Sfn.

Дослідження в галузі алгебри почалися в 1950-х роках. Досліджувалися питання про подання квадратних матриць, про аналіз некомпактных простих груп Лі, про дослідження тотожностей другого степеня в універсальних алгебрах і в алгебрах другого степеня та іншіШаблон:Sfn. Систематичне застосування нескінченних систем рівнянь до розв'язування конкретних задач математичної фізики і в зв'язку з цим розвиток методів дослідження і розв'язування систем, що тут виникають, здійснені у працях вірменських математиків: Б. Л. Абраамяна, Е. А. Александрян, Н. Х. Арутюняна, Н. О. Гулканян, М. М. Джрбащяна, Б. А. Костандяна, Р. С. Мінасяна, О. М. Сапонджяна, М. С. Саркісяна, К. С. ЧобанянаШаблон:Sfn.

XXI століття

В сьогоднішній час у Вірменії основні математичні дослідження ведуться в Інституті математики НАН РВ і в Єреванському державному університеті. У перші роки роботи Інститут математики НАН РВ займався переважно теорією функцій. З часом сфера досліджень розширилася і в даний час включає комплексний аналіз, дійсний аналіз, диференціальне та інтегральне числення, теорію ймовірностей, математичну статистику, математичну фізику[5].

В сучасній Вірменії видаються такі математичні журнали: «Вісті НАН Вірменії: Математика» (Національна академія наук Республіки Вірменія, головний редактор — Артур Саакян)[6], Вірменський журнал математики (Національна академія наук Республіки Вірменія, головний редактор — Анрі Нерсісян)[7], Математика у вищій школі (Національний політехнічний університет Вірменії, головний редактор — Ванік Захарян), «Вісник ЄДУ. Серія фізики і математики» (Єреванський державний університет, головний редактор — Варужан Атабекян)[8], також діє Вірменський математичний союз, який об'єднує математиків країни[9].

Примітки

Шаблон:Примітки

Література

Шаблон:Refbegin

Шаблон:Refend

  1. ↑ Шаблон:Cite web
  2. ↑ Шаблон:БСЭ
  3. ↑ Шаблон:Cite web
  4. ↑ Шаблон:Cite web
  5. ↑ Шаблон:Cite web
  6. ↑ Шаблон:Cite web
  7. ↑ Шаблон:Cite web
  8. ↑ Шаблон:Cite web
  9. ↑ Шаблон:Cite web
Отримано з https://uk.wiki.beta.math.wmflabs.org/w/index.php?title=Історія_математики_у_Вірменії&oldid=7975