Описаний чотирикутник
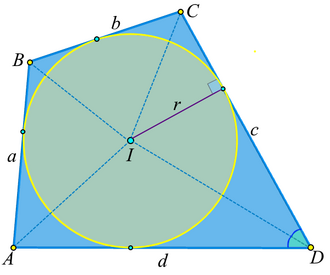
В Евклідовій геометрії описаний чотирикутникШаблон:SfnШаблон:Rp — опуклий чотирикутник, усі сторони якого є дотичними до кола, розташованого всередині чотирикутника. Також має назву дотичний чотирикутник (Шаблон:Lang-en).[1]Шаблон:Rp
Саме коло називається вписаним колом чотирикутника, а його центр I — інцентром.
Центр вписаного в чотирикутник кола лежить на перетині бісектрис чотирьох його внутрішніх кутів.
Описаний чотирикутник є окремим випадком описаного багатокутника.
Особливі випадки
Не кожен чотирикутник можна описати навколо кола. Прикладом чотирикутника, який не можна описати навколо кола, є прямокутник, який не є квадратом.
Будь-який дельтоїд (в тому числі і ромб, квадрат) можна описати навколо кола.Шаблон:SfnШаблон:Rp Дельтоїди також є зовні-описаними чотирикутниками, та чотирикутниками з перпендикулярними діагоналями (ортодіагональними).[2]
В трапецію можна вписати коло, якщо сума довжин її основ рівна сумі довжин її бокових сторін.
Біцентричний чотирикутник — це вписаний чотирикутник, який також є описаним. Прикладом може бути прямокутний дельтоїд, або рівнобічна трапеція, у якої висота є середнім геометричним між її основами.
Умови, за яких чотирикутник є описаним
У цьому розділі наведено необхідні та достатні умови, щоб чотирикутник був описаним.
- Опуклий чотирикутник можна описати тоді й лише тоді, коли чотири бісектриси його внутрішніх кутів є конкурентними, тобто, перетинаються в одній точці.[3]Шаблон:Rp
Ця спільна точка є центром вписаного кола. Також в цій точці перетинаються бісектриси внутрішніх кутів, утворених при перетині прямих, що містять протилежні сторони чотирикутника.
- Сума протилежних сторін.
Згідно з теоремою Піто:Шаблон:SfnШаблон:Rp[3]Шаблон:Rp [4]Шаблон:Rp[5]
Опуклий чотирикутник Шаблон:Math з послідовними сторонами a, b, c, d можна описати навколо кола тоді і лише тоді, коли суми його протилежних сторін рівні.
- Те, що це твердження є також і достатньою умовою, було доведено Якобом Штейнером у 1846 році.[5]
Має місце і зворотня теорема, яка запропонована також Я.ШтейнеромШаблон:SfnШаблон:Rp :
- Якщо суми протилежних сторін чотирикутника рівні, то цей чотирикутник є описаним навколо деякого кола.

Перетин протилежних сторін описаного чотирикутника
- Якщо протилежні сторони опуклого чотирикутника ABCD, який не є трапецією, перетинаються в точках E та F (прямі АВ і CD перетинаються в E, а прямі AD і BC перетинаються в F), то чотирикутник є описаним тоді і лише тоді, коли:[3]Шаблон:Rp
або

- Ще одна необхідна і достатня умова полягає в тому, що опуклий чотирикутник ABCD є описаним тоді і тільки тоді, коли кола, вписані в два трикутники ABC і ADC (або ABD i BCD), дотичні одне до одного.[5]Шаблон:Rp
- Діагоналі опуклого чотирикутника ABCD при перетині ділять його на чотири трикутники ∆ABD, ∆ABC , ∆BCD, ∆ACD. Кола, вписані в ці трикутники, дотикаються до сторін чотирикутника у восьми точках, по дві на кожну сторону. Чотирикутник є описаним чотирикутником тоді і тільки тоді, коли суми відстаней між точками дотику на протилежних сторонах чотирикутника рівні:[5]Шаблон:Rp
- У 1954 році Маріус Йосіфеску (Marius Iosifescu) довів, що опуклий чотирикутник має вписане коло тоді і тільки тоді, коли[6]

- Крім того, опуклий чотирикутник з послідовними сторонами a, b, c, d є описаним тоді і тільки тоді, коли:
де Ra, Rb, Rc, Rd — радіуси вписаних ззовні кіл чотирикутника ABCD, які зовнішньо дотикаються до сторін a, b, c, d відповідно, і продовжень двох суміжних сторін для кожної сторони.[7]Шаблон:Rp
Формули для описаного чотирикутника
Площа
Нетригонометричні формули
- Площу описаного чотирикутника ABCD зі сторонами a, b, c, d можна знайти за формулою:
де r — радіус вписаного кола, — півпериметр чотирикутника ABCD.
Ця формула площі справедлива для всіх описаних багатокутників.
- Формула площі описаного чотирикутника ABCD через його сторони a, b, c, d та діагоналі p та q:[4]Шаблон:Rp
Оскільки тоді і тільки тоді, коли описаний чотирикутник ABCD також є вписаним, тобто ABCD — біцентричний[8]Шаблон:Rp , то з формули видно, що описаний чотирикутник має максимальну площу тоді і тільки тоді, коли він є біцентричним.
Тригонометричні формули
- Формула площі описаного чотирикутника ABCD через його сторони a, b, c, d та два протилежних кута:[4]Шаблон:Rp[9][10]Шаблон:Rp[11]Шаблон:Rp
Для заданих довжин сторін площа є максимальною, коли чотирикутник також є вписаним і, отже, біцентричним чотирикутником. Для нього: , а отже,
- Формула площі описаного чотирикутника ABCD через дві сусідні сторони та два протилежних кута:[4]Шаблон:Rp
- Формула площі описаного чотирикутника ABCD через сторони a, b, c, d та кут між діагоналями:[4]Шаблон:Rp
Цю формулу не можна використовувати для дельтоїдів, оскільки в них діагоналі перпендикулярні: θ = 90°, і функція тангенса не визначена.
- Формула площі описаного чотирикутника ABCD через відстані від його вершин до центра вписаного кола I та два протилежних кута:[10]Шаблон:Rp
Нерівності, пов'язані з площею
Як опосередковано зазначено вище, площа описаного чотирикутника зі сторонами a, b, c, d задовольняє нерівності:
Рівність досягається тільки для біцентричного чотирикутника.
За Т. А. Івановою (1976 р.), півпериметр p описаного чотирикутника задовольняє нерівності:
де r — радіус вписаного кола. Рівність досягається тоді і тільки тоді, коли чотирикутник є квадратом.
Це означає, що для площі K = r p існує нерівність
де рівність досягається тоді і тільки тоді, коли описаний чотирикутник є квадратом.
Радіус вписаного кола
Радіус вписаного кола описаного чотирикутника ABCD зі сторонами a, b, c, d та площею S, можна обчислити за формулою:[4] Шаблон:Rp
Описаний чотирикутник з даними сторонами має максимальний радіус вписаного кола, якщо чотирикутник є одночасно і вписаним (тобто біцентричним).

Радіус вписаного кола також можна виразити через відстані від центру кола I до вершин описаного чотирикутника ABCD. Якщо u = AI, v = BI, x = CI і t = DI, то[12]:
де .
Радіус вписаного кола описаного чотирикутника ABCD через довжини дотичних відрізків e, f, g, h:[8]Шаблон:Rp[13]
Діагоналі описаного чотирикутника
Якщо e, f, g та h — довжини дотичних до вписаного кола з вершин описаного чотирикутника A, B, C та D відповідно, а p = AC та q = BD — його діагоналі, то:[8]Шаблон:Rp
Формули кутів
Якщо e, f, g та h — довжини дотичних до вписаного кола з вершин описаного чотирикутника A, B, C та D відповідно, то кути чотирикутника можна знайти за формулами:[2] Шаблон:Rp
Чотирикутник, утворений точками дотику вписаного кола до сторін описаного чотирикутника

Вписане в чотирикутник ABCD коло торкається до його сторін в чотирьох точках. Ці чотири точки формують новий чотирикутник усередині початкового, який є вписаним у вписане коло початкового чотирикутника.
Дві хорди («k» і «l» на малюнку) вписаного кола чотирикутника ABCD, що сполучають точки дотику вписаного кола на протилежних сторонах описаного чотирикутника, також є діагоналями контактного чотирикутника.
Довжини цих хорд:[2] Шаблон:Rp
де хорда довжиною k сполучає сторони чотирикутника a = e + f і c = g + h, а хорда довжиною l — сторони чотирикутника b = f + g і d = h + e.
Кут між хордами вписаного кола k та l :[2] Шаблон:Rp
де e, f, g та h довжини дотичних до вписаного кола з вершин описаного чотирикутника A, B, C та D відповідно.
Хорди k та l:
- перпендикулярні тоді і тільки тоді, коли описаний чотирикутник ABCD також є вписаним (тобто біцентричним).[2]Шаблон:Rp
- мають однакову довжину тоді і тільки тоді, коли описаний чотирикутник ABCD є дельтоїдом.[1]Шаблон:Rp
Якщо описаний чотирикутник ABCD має точки дотику W до AB і Y до CD, і якщо хорда WY перетинає діагональ BD у точці M, то відношення довжин дотичних дорівнює відношенню відрізків діагоналі BD.[14]
Властивості

- Якщо чотирикутник описано навколо кола, то існує точка, рівновіддалена від усіх його сторін (центр вписаного кола). Щоб знайти цю точку, достатньо знайти точку перетину бісектрис двох сусідніх кутів цього чотирикутника.
- Всі сторони описаного чотирикутника є дотичними до кола
- Перпендикуляр, опущений з центра вписаного кола на будь-яку сторону описаного чотирикутника дорівнює радіусу кола.
- Відрізки дотичних до вписаного кола, проведені з однієї вершини, рівні.
- Чотири відрізки між центром вписаного кола та точками дотику до чотирикутника розділяють чотирикутник на чотири прямокутних дельтоїда .
- Якщо пряма розділяє описаний чотирикутник на два багатокутника з рівними площами та рівними периметрами, то ця пряма проходить через центр вписаного кола.[3]
Колінеарні точки

Нехай точки M та N — середини діагоналей описаного чотирикутника ABCD , I — центр його вписаного кола, точка K — центр відрізка FE, який сполучає точки перетину прямих, що містять протилежні сторони чотирикутника. Тоді, точки M, N, K та I є колінеарними, тобто лежать на одній прямій.[3]Шаблон:Rp Ця пряма називається прямою Ньютона чотирикутника ABCD.
Також на цій прямій лежить вершинний центроїд Gv чотирикутника ABCD (точка перетину бімедіан чотирикутника; центр тяжіння рівних мас, зосереджених у вершинах чотирикутника), причому точка Gv знаходиться в середині відрізка MN.
Якщо прямі, що містять протилежні сторони описаного чотирикутника ABCD перетинаються в точках F та E, а прямі, що містять протилежні сторони чотирикутника, сформованого точками дотику вписаного кола до сторін ABCD, перетинаються в точках L та M, то чотири точки F, E, L і M колінеарні.[15]Шаблон:Rp

Якщо вписане коло дотикається до сторін AB, BC, CD, DA у точках T1, T2, T3, T4 відповідно, і якщо N1, N2, N3, N4 є ізотомічно спряженими точками цих точок відносно відповідних сторін (тобто , AT1 = BN1 і так далі), то точка Нагеля описаного чотирикутника визначається як перетин прямих N1N3 та N2N4. Обидві ці лінії ділять периметр чотирикутника навпіл.
Що ще важливіше, точка Нагеля N, «центроїд площі» G і центр вписаного кола I колінеарні в цьому порядку, і NG = 2GI.
Ця пряма називається лінією Нагеля описаного чотирикутника.[16]
В описаному чотирикутнику ABCD із центром вписаного кола I, діагоналі перетинаються в точці P.
Нехай HX, HY, HZ, HW — ортоцентри трикутників AIB, BIC, CID, DIA. Тоді точки P, HX, HY, HZ, HW колінеарні.:[10]Шаблон:RpШаблон:Clear
Конкурентні прямі
Дві діагоналі описаного чотирикутника та дві хорди вписаного кола, що сполучають точки дотику на протилежних сторонах є конкурентні, тобто перетинаються в одні точці.[11][10]Шаблон:Rp
Один із способів довести це — граничний випадок теореми Бріаншона, яка стверджує, що шестикутник, усі сторони якого є дотичними до однієї коніки має три діагоналі, які перетинаються в одній точці. З описаного чотирикутника можна сформувати шестикутник із двома кутами 180°, розмістивши дві нові вершини у двох протилежних точках дотику; усі шість сторін цього шестикутника лежать на прямих, дотичних до вписаного кола, тому його діагоналі перетинаються в одній точці. Але дві з цих діагоналей збігаються з діагоналями описаного чотирикутника, а третя діагональ шестикутника є прямою, що проходить через дві протилежні точки дотику. Аналогічно доводиться перетин з хордою, що сполучає дві інші точки дотику.
Якщо продовження протилежних сторін описаного чотирикутника перетинаються в точках F і E, а діагоналі перетинаються в точці P, то пряма FE перпендикулярна до прямої, що містить відрізок IP , де I — центр вписаного кола.[15]Шаблон:Rp
Центр вписаного кола
Центр вписаного кола описаного чотирикутника лежить на його прямій Ньютона (пряма, що проходить через середини діагоналей)..[17]Шаблон:Rp
Якщо I — центр вписаного кола чотирикутника ABCD, то виконуються наступні рівності:
- 2. Добуток двох суміжних сторін:[18]
- 4. Центр вписаного кола I в описаному чотирикутнику ABCD збігається з «центроїдом вершин» чотирикутника тоді і тільки тоді, коли:[10]Шаблон:Rp
- 5. Якщо M і N є серединами діагоналей AC і BD відповідно в описаному чотирикутнику ABCD з центром вписаного кола I, тоді[10]Шаблон:Rp[19]
де e, f, g і h — довжини дотичних в вершинах A, B, C і D відповідно.
Поєднуючи першу рівність із попередньою властивістю, отримаємо що «центроїд вершини» описаного чотирикутника збігається з центром вписаного кола тоді і тільки тоді, коли центр вписаного кола є серединою відрізка MN, що з'єднує середини діагоналей.
- Якщо чотириланковий механізм зроблено у формі описаного чотирикутника, то він залишатиметься описаним при будь-якому положенні його ланок, за умови, що чотирикутник залишається опуклим.[20][21] (Таким чином, наприклад, якщо квадрат деформується в ромб, він залишається дотичним, хоча до меншого вписаного кола). Якщо одна сторона утримується у фіксованому положенні, то при деформації чотириланкового механізма центр вписаного кола окреслює коло радіусом , де a, b,c, d — сторони чотирикутника, а «p» — півпериметр.
Співвідношення у трикутниках, утворених при перетині діагоналей

Діагоналі описаного чотирикутника ABCD перетинаються в точці P, і розбивають його на чотири трикутники APB, BPC, CPD, DPA
Нехай r1, r2, r3, та r4 — радіуси вписаних в ці трикутники кіл. Чао та Симеонов довели, що чотирикутник є описаним тоді і тільки тоді, коли:[22]
Ця властивість була доведена за п'ять років до того Вейштейном .[1]Шаблон:Rp[23]
Нехай h1, h2, h3, та h4 — висоти цих же трикутників, проведені з точки P на сторони описаного чотирикутника ABCD. Чотирикутник є описаним тоді і тільки тоді, коли:[6][23]
Нехай ra, rb, rc, та rd — радіуси зовнівписаних кіл цих же трикутників (кола торкаються до відповідної сторони чотирикутника та продовжень його діагоналей). Чотирикутник є описаним тоді і тільки тоді, коли:[5] Шаблон:Rp
Якщо R1, R2, R3, та R4 — радіуси описаних кіл трикутників APB, BPC, CPD, DPA відповідно, то чотирикутник є описаним тоді і тільки тоді, коли:[24]Шаблон:Rp
У 1996 році Вайнштейн був, мабуть, першим, хто довів ще одну цікаву властивість описаних чотирикутників, яка пізніше з'явилася в кількох журналах і на веб-сайтах.[5] Шаблон:Rp В ній стверджується, що центри вписаних кіл у трикутники APB, BPC, CPD, DPA є конциклічними тоді і тільки тоді, коли чотирикутник описаний. Фактично, центри цих вписаних кіл утворюють ортодіагональний вписаний чотирикутник.:[5] Шаблон:Rp
Пов'язаним результатом є те, що вписані кола можна замінити на зовнівписані кола до тих самих трикутників (дотичні до сторін чотирикутника та продовжень його діагоналей). Таким чином, опуклий чотирикутник ABCD є описаним тоді і тільки тоді, коли центри зовнівписаних в трикутники APB, BPC, CPD, DPA кіл є вершинами вписаного чотирикутника (тобто лежать на одному колі). :[5] Шаблон:Rp
Якщо Ea, Eb, Ec, та Ed центри зовнівписаних кіл в трикутники APB, BPC, CPD, та DPA відповідно, до сторін трикутників, що протилежні вершинам B і D (дотичні до діагоналі чотирикутника ABCD, продовження його сторони та продовження іншої діагоналі), то опуклий чотирикутник ABCD є описаним тоді і тільки тоді, коли точки Ea, Eb, Ec, та Ed лежать на одному колі. :[5] Шаблон:Rp
Якщо Ra, Rb, Rc, та Rd — радіуси цих зовнівписаних кіл, то опуклий чотирикутник ABCD є описаним тоді і тільки тоді, коли:[5] Шаблон:Rp
Опуклий чотирикутник ABCD є описаним тоді і тільки тоді, коли:[6]
де S — площі відповідних трикутників.
Нехай точка P перетину діагоналей чотирикутника розбиває діагональ АС на відрізки AP = p1 та PC = p2 , а діагональ BD на відрізки BP = q1 та PD = q2. Опуклий чотирикутник ABCD є описаним тоді і тільки тоді, коли виконується рівність:[25]
Умови, за яких описаний чотирикутник є певним видом чотирикутників
Ромб
Описаний чотирикутник є ромбом тоді і тільки тоді, коли його протилежні кути рівні. Зокрема, якщо протилежні кути прямі, то описаний чотирикутник є квадратом.
Дельтоїд
Описаний чотирикутник є дельтоїдом тоді і тільки тоді, коли виконується будь-яка з наступних умов:
- Площа дорівнює половині добутку діагоналей.
- Діагоналі перпендикулярні.
- Дві хорди вписаного кола, що з'єднують протилежні точки дотику до сторін чотирикутника, мають однакову довжину.
- Суми довжин дотичних до вписаного кола, що проведені з протилежних вершин рівні.
- Бімедіани чотирикутника рівні.
- Добутки протилежних сторін рівні.
- Центр вписаного кола лежить на діагоналі, яка є віссю симетрії.
Трапеція
Якщо вписане коло торкається до сторін AB та CD в точках W та Y відповідно, то описаний чотирикутник ABCD є трапецією з паралельними сторонами AB та CD тоді і тільки тоді, коли[26]Шаблон:Rp
а AD та BC є паралельними сторонами трапеції тоді і тільки тоді, коли
Біцентричний чотирикутник

Нехай вписане коло торкається до сторін чотирикутника AB, BC, CD, DA в точках W, X, Y, Z відповідно, тоді описаний чотирикутник ABCD є також і вписаним (а значить біцентричним) тоді і тільки тоді, коли виконується будь-яка з наступних умов:[2]Шаблон:Rp[15][27]
- WY перпендикулярний до XZ
Перша умова з цих трьох означає, що чотирикутник WXYZ є ортодіагональним чотирикутником.
Описаний чотирикутник є біцентричним тоді і тільки тоді, коли радіус його вписаного кола більший за радіус будь-якого іншого описаного чотирикутника з такою ж послідовністю довжин сторін.[28]Шаблон:Rp Шаблон:Clear
Див. також
- Вписаний чотирикутник
- Біцентричний чотирикутник
- Описаний багатокутник
- Вписане коло
- Теорема Ньютона
- Теорема Енна
Примітки
Література
- Шаблон:Книга
- Michael de Villiers The Tangential or Circumscribed Quadrilateral RUMEUS, University of Stellenbosch, Learning and Teaching Mathematics, No. 29, 2020, pp. 39-45
Посилання
- ↑ 1,0 1,1 1,2 Шаблон:Citation
- ↑ 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 Шаблон:Citation.
- ↑ 3,0 3,1 3,2 3,3 3,4 Шаблон:Citation.
- ↑ 4,0 4,1 4,2 4,3 4,4 4,5 Шаблон:Citation
- ↑ 5,00 5,01 5,02 5,03 5,04 5,05 5,06 5,07 5,08 5,09 5,10 5,11 Шаблон:Citation
- ↑ 6,0 6,1 6,2 Шаблон:Citation.
- ↑ Шаблон:Citation
- ↑ 8,0 8,1 8,2 Шаблон:Citation
- ↑ Шаблон:Citation.
- ↑ 10,0 10,1 10,2 10,3 10,4 10,5 10,6 10,7 Шаблон:Citation
- ↑ 11,0 11,1 Шаблон:Citation
- ↑ Шаблон:Citation.
- ↑ Шаблон:Citation.
- ↑ Шаблон:Cite web
- ↑ 15,0 15,1 15,2 Шаблон:Citation.
- ↑ Шаблон:Citation.
- ↑ Шаблон:Citation.
- ↑ Шаблон:Citation.
- ↑ «Determine ratio OM/ON», Post at Art of Problem Solving, 2011Шаблон:Недоступне посилання
- ↑ Шаблон:Citation.
- ↑ Шаблон:Cite web
- ↑ Шаблон:Citation.
- ↑ 23,0 23,1 Шаблон:Citation
- ↑ Шаблон:Citation.
- ↑ Шаблон:Citation.
- ↑ Шаблон:Citation.
- ↑ Шаблон:Citation.
- ↑ Шаблон:Citation.