Спряжені функтори

Спря́жені функтори — пара функторів, що перебувають у певному співвідношенні між собою. Спряжені функтори часто зустрічаються в різноманітних галузях математики.

Неформально, функтори Шаблон:Math і Шаблон:Math є спряженими, якщо вони задовольняють співвідношенню $\mathrm{H}\mathrm{o}\mathrm{m}(F(X),Y)=\mathrm{H}\mathrm{o}\mathrm{m}(X,G(Y))$. Тоді Шаблон:Math називається лівим спряженим функтором, а Шаблон:Math — правим.

Мотивація

Спряжені функтори — один з ключових інструментів теорії категорій, багато важливих математичних конструкцій можна описати як спряжені функтори. В результаті із загальних теорем про спряжені функтори, таких як еквівалентність різних означень, і з того факту, що праві спряжені функтори комутують з границями (а ліві — з кограницями), можуть негайно випливати доведення багатьох цікавих результатів.

Розв'язок оптимізаційної задачі

Можна сказати, що спряжений функтор є способом вказівки найбільш ефективного розв'язку певної задачі за допомогою стандартного методу. Наприклад, елементарна проблема з теорії кілець — вкладення кільця без одиниці у кільце з одиницею. Найбільш ефективним способом це зробити є додавання в кільце одиниці, всіх елементів, необхідних для виконання аксіом кільця (наприклад, елементи типу Шаблон:Math, де Шаблон:Math — елемент кільця) без припущення якихось співвідношень в новому кільці, які не потрібні для виконання аксіом. Ця конструкція є стандартною в тому сенсі, що вона працює для будь-якого кільця без одиниці.

Наведений вище опис є дуже розпливчастим але його можна зробити точним, використовуючи мову теорії категорій: конструкція є «найбільш ефективною», якщо вона задовольняє універсальні властивості, і «стандартною» в тому сенсі, що вона задає функтор. Універсальні властивості діляться на початкові і термінальні і оскільки ці поняття є двоїстими, досить розглянути одне з них.

Ідея використання початкової властивості полягає в тому щоб сформулювати проблему в термінах такої допоміжної категорії Шаблон:Math, щоб залишилося лише знайти початковий об'єкт Шаблон:Math. Таке формулювання має ту перевагу, що завдання «знаходження найбільш ефективного розв'язку» стає чітким і в якомусь сенсі подібним до завданням знаходження екстремуму. Для вибору правильної категорії Шаблон:Math іноді потрібно підбирати непрості прийоми: у випадку півкільця Шаблон:Math потрібна категорія — це категорія, об'єкти якої — гомоморфізми кілець Шаблон:Math, де Шаблон:Math — деяке кільце з одиницею. Морфізм в Шаблон:Math між Шаблон:Math і Шаблон:Math — комутативні трикутники виду Шаблон:Math, де Шаблон:Math — гомоморфізм кілець. Існування морфізма між Шаблон:Math і Шаблон:Math означає, що Шаблон:Math є не менш ефективним розв'язком задачі, ніж Шаблон:Math має більше доданих елементів і (або) більше співвідношень між ними, ніж Шаблон:Math.

Метод визначає «найбільш ефективний» і «стандартний» розв'язок задач, якщо він задає спряжені функтори.

Формальні означення

Існують кілька еквівалентних означень спряжених функторів. Їх еквівалентність є елементарною але не тривіальною.

Означення за допомогою універсальної стрілки Шаблон:Перехід легко сформулювати, воно також найближче до інтуїції з приводу «оптимізаційної задачі».

Означення за допомогою одиниці і коодиниці Шаблон:Перехід є зручно для функторів, часто зустрічаються в алгебрі, тому що використовує формули, які можна перевірити безпосередньо.

Означення за допомогою [[Функтор Hom|множин Шаблон:Math]] Шаблон:Перехід робить очевидною симетричність означення і прояснює причини для через які функтори називаються «спряженими».

Універсальна стрілка

Функтор Шаблон:Math називається лівим спряженим функтором, якщо для кожного об'єкта Шаблон:Math категорії Шаблон:Math існує термінальна стрілка Шаблон:Math з Шаблон:Math у Шаблон:Math. Якщо для кожного Шаблон:Math у Шаблон:Math вибрати об'єкт Шаблон:Math у Шаблон:Math, для якого визначена термінальна стрілка Шаблон:Math, то існує єдиний функтор Шаблон:Math , такий, що Шаблон:Math і для будь-якого морфізма в категорії Шаблон:Math Шаблон:Math виконується Шаблон:Math; Шаблон:Math тоді називають лівим спряженим до функтора Шаблон:Math.

Функтор Шаблон:Math називається правим спряженим функтором, якщо для кожного об'єкта Шаблон:Math категорії Шаблон:Math існує початкова стрілка з Шаблон:Math у Шаблон:Math. Якщо для кожного Шаблон:Math у Шаблон:Math вибрати об'єкт Шаблон:Math у Шаблон:Math, такий, що визначена початкова стрілка Шаблон:Math з Шаблон:Math в Шаблон:Math, то існує єдиний функтор Шаблон:Math, такий, що Шаблон:Math і Шаблон:Math для Шаблон:Math — морфізма у Шаблон:Math; Шаблон:Math тоді називають правим спряженим до функтора Шаблон:Math.

Функтор Шаблон:Math є лівим спряженим для Шаблон:Math тоді і тільки тоді, коли Шаблон:Math є правим спряженим для Шаблон:Math. Однак це не очевидно з означення через універсальну стрілку але очевидно завдяки означенню через одиницю і коодиницю.

Одиниця і коодиниця

Для задання одиниці і коодиниці в категоріях Шаблон:Math і Шаблон:Math потрібно зафіксувати два функтори Шаблон:Math і два натуральні перетворення:

$\begin{array}{cc}\epsilon & :FG\to 1_{𝒞}\\ \eta & :1_{𝒟}\to GF\end{array}$,

що називаються відповідно коодиницею і одиницею спряження, таких, що композиції

$F\stackrel{F\eta }{\to }FGF\stackrel{\epsilon F}{\to }F$ і

$G\stackrel{\eta G}{\to }GFG\stackrel{G\epsilon }{\to }G$

є тотожними перетвореннями Шаблон:Math і Шаблон:Math функторів Шаблон:Math і Шаблон:Math відповідно.

У такій ситуації Шаблон:Math є лівим спряженим для Шаблон:Math і Шаблон:Math є правим спряженим для Шаблон:Math. Іноді це відношення позначають $(\epsilon ,\eta ):F⊣G$ або просто $F⊣G$.

У формі рівнянь наведені вище умови на Шаблон:Math називаються рівняннями коодиниці і одиниці:

$\begin{array}{cc}{1}_F& =\epsilon F\circ F\eta \\ 1_G& =G\epsilon \circ \eta G\end{array}$

Означення через функтори Hom

Розглянемо два функтори Шаблон:Math і Шаблон:Math . Нехай існує натуральний ізоморфізм:

$\mathrm{\Phi }:{\mathrm{h}\mathrm{o}\mathrm{m}}_C(F-,-)\to {\mathrm{h}\mathrm{o}\mathrm{m}}_D(-,G-)$.

Він визначає сім'ю бієкцій:

${\mathrm{\Phi }}_{Y,X}:{\mathrm{h}\mathrm{o}\mathrm{m}}_C(FY,X)\to {\mathrm{h}\mathrm{o}\mathrm{m}}_D(Y,GX)$.

для всіх об'єктів Шаблон:Math у Шаблон:Math і Шаблон:Math у Шаблон:Math .

Тут Шаблон:Math називається лівим спряженим для Шаблон:Math і Шаблон:Math — правим спряженим для Шаблон:Math.

Щоб зрозуміти, що мається на увазі під натуральністю Шаблон:Math, потрібно пояснити, яким чином Шаблон:Math і Шаблон:Math є функторами. Насправді, вони обидва є біфункторами з Шаблон:Math у Шаблон:Math. В явному вигляді натуральність Шаблон:Math означає, що для всіх морфізмів Шаблон:Math у Шаблон:Math і морфізма Шаблон:Math у Шаблон:Math діаграма нижче комутує:

Naturality of Φ

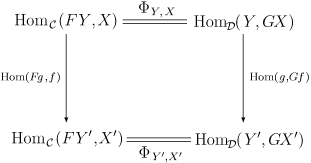
Вертикальні стрілки на діаграмі породжуються композиціями морфізмів. Наприклад, для h у Hom_C(FY, X) за означенням Hom(Fg, f) : Hom_C(FY, X) → Hom_C(FY′, X′) задається як h → f o h o Fg . Подібним є і означення Hom(g, Gf).

В інший спосіб можна описати натуральність так, що для всіх об'єктів Шаблон:Math у Шаблон:Math і Шаблон:Math у Шаблон:Math, для всіх морфізмів h у Hom_C(FY, X) і Шаблон:Math

${\mathrm{\Phi }}_{Y,X^{\prime }}(f\circ h)=G(f)\circ {\mathrm{\Phi }}_{Y,X}(h)$

і для всіх морфізмів j у Hom_C(Y , GX) і Шаблон:Math:

${\mathrm{\Phi }}_{Y^{\prime },X}^{-1}(j\circ g)={\mathrm{\Phi }}_{Y,X}^{-1}\circ F(g).$

Приклади

Вільні групи

Конструкція вільної групи є зручним прикладом для прояснення суті означень. Нехай Шаблон:Math — функтор, який множині Шаблон:Math зіставляє вільну групу, породжену елементами Шаблон:Math, і Шаблон:Math — забуваючий функтор, що зіставляє групі Шаблон:Math її множину-носій. Тоді Шаблон:Math — лівий спряжений для Шаблон:Math:

Термінальні стрілки: для кожної групи Шаблон:Math, група Шаблон:Math — вільна група, породжена елементами Шаблон:Math як множиною. Нехай ${\epsilon }_X:FGX\to X$ — гомоморфізм груп, який переводить породжуючі елементи Шаблон:Math у відповідні елементи Шаблон:Math. Тоді $(GX,{\epsilon }_X)$ — термінальний морфізм з Шаблон:Math у Шаблон:Math, тому що будь-який гомоморфізм з вільної групи Шаблон:Math в Шаблон:Math розкладається через ${\epsilon }_X:FGX\to X$ за допомогою єдиної функції з множини Шаблон:Math в множину Шаблон:Math. Це означає, що Шаблон:Math — пара спряжених функторів.

Множині Hom відображення з вільної групи Шаблон:Math у групу Шаблон:Math однозначно відповідають відображенням множини Шаблон:Math у множину Шаблон:Math: кожен гомоморфізм однозначно визначається своїми значеннями на породжуючих елементах вільної групи. Прямим обчисленням можна перевірити, що ця відповідність — натуральне перетворення, а тому, пара Шаблон:Math є спряженою.

Подальші приклади з алгебри

• Всі вільні об'єкти — результати застосування вільного функтора, який є лівим спряженим для забуваючого функтора.
• добутки, ядра і вирівнювачі — приклади категорних границь. Всі такі функтори є правими спряженими до діагонального функтора. Аналогічно, кодобуток, коядра і ковирівнювачі є кограницями і є лівими спряженими до діагонального функтора.
• Додавання одиниці в кільце без одиниці (приклад з розділу «Мотивація»). Якщо задано кільце без одиниці Шаблон:Math, то відповідне йому кільце з одиницею — добуток Шаблон:Math, на якому задано [[Білінійне відображення|Шаблон:Math-білінійний]] добуток за формулою Шаблон:Math. Побудований функтор є спряженим зліва до забуваючого функтора, що відправляє кільце з одиницею в те ж кільце у категорії кілець, що можуть не мати одиниці.
• Розширення кілець. Нехай Шаблон:Math і Шаблон:Math — кільця, і Шаблон:Math — гомоморфізм кілець . Тоді Шаблон:Math можна розглядати як (лівий) Шаблон:Math-модуль, і тензорний добуток з Шаблон:Math визначає функтор Шаблон:Math. Тоді Шаблон:Math є спряженим зліва до забуваючого функтора Шаблон:Math.
• Тензорні добутки. Якщо Шаблон:Math — кільце і Шаблон:Math — правий Шаблон:Math-модуль, то тензорний добуток з Шаблон:Math визначає функтор Шаблон:Math. Функтор Шаблон:Math, визначений як Шаблон:Math є спряженим справа до Шаблон:Math.
• Поле часток. Для категорії Шаблон:Math областей цілісності і ін'єктивних гомоморфізмів, забуваючий функтор Шаблон:Math має лівий спряжений, що зіставляє кожній області цілісності її поле часток.
• Кільця многочленів . Для Шаблон:Math — категорії комутативних кілець із зазначеним елементом і гомоморфізмів, що зберігають зазначений елемент, забуваючий функтор Шаблон:Math має лівий спряжений — він зіставляє кільцю Шаблон:Math пару Шаблон:Math, де Шаблон:Math — кільце многочленів з коефіцієнтами з Шаблон:Math.
• Забуваючий функтор Шаблон:Math із категорії груп у групу моноїдів має як лівий спряжений, так і правий спряжений функтори. Лівий спряжений зіставляє моноїду Шаблон:Math групу Шаблон:Math, яку можна одержати як факторгрупу вільної групи породженої елементами $[m],m\in M,$по нормальній підгрупі породженій елементами виду $[mn][n{]}^{-1}[m{]}^{-1},m,n\in M.$ Правий спряжений функтор зіставляє моноїду його підгрупу оборотних елементів.
• Абелізація. Забуваючий функтор Шаблон:Math має лівий спряжений, що називається функтором абелізаціі, який кожній групі Шаблон:Math зіставляє факторгрупу по комутанту: Шаблон:Math. Для групи Шаблон:Math її абелізація має універсальну властивість: кожен гомоморфізм $\phi$ із Шаблон:Math у абелеву групу Шаблон:Math однозначно записується як $\phi =\overline{\phi }\circ \mu ,$ де $\mu$ є відображенням факторизації $\mu :G\to G^{ab},$ а $\overline{\phi }$ — однозначно визначеним гомоморфізмом абелевих груп.

Бієкцію між множинами Шаблон:Math і Шаблон:Math задається так: гомоморфізму абелевих груп $\psi :G^{ab}\to A$ відповідає гомоморфізм $\psi \circ \mu ,$ а гомоморфізму $\phi$ із Шаблон:Math у абелеву групу Шаблон:Math, визначений вище гомоморфізм $\overline{\phi }.$

Приклади з топології

• Функтор з двома спряженими. Нехай Шаблон:Math — функтор, що зіставляє топологічному простору його множину-носій (тобто забуває топологію). У Шаблон:Math є лівий спряжений Шаблон:Math, який надає множині дискретну топологію, і правий спряжений Шаблон:Math, який надає множині тривіальну топологію.
• Надбудова і простір петель. Для даних топологічних просторів Шаблон:Math і Шаблон:Math можна побудувати простір Шаблон:Math класів гомотопії відображень з надбудови Шаблон:Math у Шаблон:Math. Він є ізоморфним простору Шаблон:Math класів гомотопії відображень з Шаблон:Math у простір петель Шаблон:Math, тому функтори надбудови і простору петель є спряженими в гомотопічній категорії топологічних просторів.
• Вкладення Шаблон:Math категорії компактних гаусдорфових просторів в категорію топологічних просторів має лівий спряжений функтор Шаблон:Math — компактифікацію Стоуна — Чеха. Коодиниця цієї пари задає неперервне відображення з довільного топологічного простору Шаблон:Math у його компактифікацію. Це відображення є вкладенням тоді і тільки тоді, коли Шаблон:Math — цілком регулярний простір.

Властивості

Існування

Не кожен функтор Шаблон:Math має лівий або правий спряжений. Якщо Шаблон:Math — повна категорія, то згідно теореми про спряжені функтори Петера Фрейда Шаблон:Math має лівий спряжений тоді і тільки тоді, коли для будь-якого Шаблон:Math з категорії Шаблон:Math існує сім'я морфізмів:

Шаблон:Math,

де індекси Шаблон:Math пробігають множина Шаблон:Math, таке, що будь-який морфізм:

Шаблон:Math

може бути записаний як:

Шаблон:Math

для деякого Шаблон:Math e Шаблон:Math і деякого морфізма:

Шаблон:Math.

Аналогічне твердження характеризує функтори, що мають правий спряжений.

Єдиність

Якщо функтор Шаблон:Math має два правих спряжених Шаблон:Math і Шаблон:Math, то Шаблон:Math і Шаблон:Math є натурально ізоморфними.

Навпаки, якщо Шаблон:Math є спряженим зліва до Шаблон:Math, і Шаблон:Math натурально ізоморфний Шаблон:Math, то Шаблон:Math також є спряженим зліва до Шаблон:Math.

Композиція

Для спряжень можна ввести композиції. Якщо Шаблон:Math — спряження між Шаблон:Math і Шаблон:Math , і Шаблон:Math — спряження між Шаблон:Math і Шаблон:Math, то функтор

$F^{\prime }\circ F:𝒞\leftarrow ℰ$

є спряженим зліва до функтора

$G\circ G^{\prime }:𝒞\to ℰ$.

Можна утворити категорію, об'єктами якої є всі малі категорії, а морфізмами — спряження.

Комутування з границями

Найбільш важлива властивість спряжених функторів — їх неперервність: кожний функтор, що має лівий спряжений (тобто є правим спряженим), комутує з границями в категорному сенсі. Відповідно, функтор, що має правий спряжений, є конеперервним, тобто комутує з кограницями. Оскільки багато конструкцій є границями або кограницями, з цього відразу випливає кілька наслідків. Наприклад:

• Застосування правого спряженого функтора до добутку дає добуток образів.
• Застосування лівого спряженого функтора до кодобутку дає кодобуток образів.
• Кожний правий спряжений і адитивний функтор між абелевими категоріями є точним зліва.
• Кожний лівий спряжений і адитивний функтор між абелевими категоріями є точним справа.

Див. також

• Зображуваний функтор
• Функтор Hom
• Категорія (математика)
• Теорія категорій

Література

• И. Букур, А. Деляну Введение в теорию категорий и функторов. — М.: Мир, 1972.
• Шаблон:Cite book
• Шаблон:Cite book
• Шаблон:Cite book
• Шаблон:Cite book