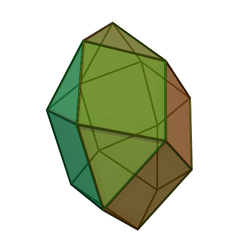
Чотирисхилий купол

У геометрії чотирисхилий купол — призматоїд, що складається з правильного восьмикутника (нижня основа купола), квадрата (верхня грань, що паралельна основі), та бічних граней: 4 прямокутників та 4 рівнобедрених трикутників.

Нижня основа також може бути напівправильним рівнокутним восьмикутником (дітетрагоном), в якому сторони рівні через одну, і всі кути рівні. При цьому сторона верхнього квадрата має бути рівною більшій стороні дітетрагона.

Належить до родини куполів і є підкласом призматоїдів.

Два куполи можуть бути з'єднані по їх нижній основі, утворюючи багатогранник Шаблон:Не перекладено, в прямій (якщо з'єднані однойменні грані) або повернутій (якщо з'єднані різнойменні грані) орієнтації.

Багатогранник Джонсона Шаблон:Math

Чотирисхилий (квадратний) купол

Тип	Багатогранник Джонсона J₄ Призматоїд, множина куполів.
Властивості	Опуклий, рівносторонній, правильногранний
Комбінаторика
Елементи	10 граней (4{3} + (4+1){4} + 1{8}) 20 ребер 12 вершин: 8 вершин (3-го степеня) + 4(4-го)
Грані	4 Правильних трикутників, 4+1 Квадратів, 1 Правильний восьмикутник.
Характеристика Ейлера	$χ = Γ - P + B = 2$
Конфігурація вершини	8(3.4.8) 4(3.4³)
Вершинна фігура	4 рівнобедрених трапецій з довжинами сторін 1, $\sqrt{2}$ , $\sqrt{2}$ та $\sqrt{2}$ 8 трикутників з довжинами сторін 1, $\sqrt{2}$ та $\sqrt{2 + \sqrt{2}}$
Класифікація
Позначення	• J₄ (в нотації Шаблон:Не перекладено) • M₅ (в нотації ЗалгаллераШаблон:Sfn) • U₄ = Q₄ Шаблон:Sfn (в Шаблон:Не перекладено) • Q₄ (в нотації Стюарта)
Символ Шлефлі	{4} \|\| t{4}
Група симетрії	Шаблон:Не перекладено, [4], (*44), порядок 8 (Циклічна симетрія 4-Піраміди)
Група обертань	C₄, [4]⁺, (44), порядок 4
Двоїстий багатогранник	Напіврозсічений чотирикутний трапецоедр
Розгортка

Рівносторонній чотирисхилий купол (або квадратний купол) є одним із багатогранників Джонсона (Шаблон:Math або Шаблон:Math (за ЗалгаллеромШаблон:Sfn).

Багатогранник Джонсона — один із 92 строго опуклих багатогранників, що мають правильні грані, але не є однорідним (тобто він не є правильним багатогранником, архімедовим тілом, призмою або антипризмою). Правильногранні багатогранники названі ім'ям Шаблон:Не перекладено, який першим перелічив їх в 1966 р. Шаблон:Sfn

Чотирисхилий купол складено з 10 граней: 4 правильних трикутників, 4+1 = 5 квадратів та 1 правильного восьмикутника.

Кожна трикутна грань оточена двома квадратами та одним восьмикутником; одна квадратна грань (верхня основа) оточена чотирма квадратами; чотири квадратні грані (бокові) оточені двома трикутними, однією квадратною та однією восьмикутною гранями; восьмикутна грань оточена чотирма трикутними та чотирма квадратними гранями.

Має 20 ребер однакової довжини. 4 ребра розташовуються між двома квадратними гранями, 8 ребер — між квадратною і трикутною гранями, 4 ребра — між трикутною і восьмикутною гранями, 4 ребра ‒ між квадратною і восьмикутною гранями.

У чотирисхилого купола 12 вершин: 4 вершини оточені трикутною і трьома квадратними гранями; 8 вершин оточені трикутною, квадратною та 8-кутною гранями.

Чотирисхилий купол можна розглядати як зріз ромбокубооктаедра, і може бути отриманий шляхом розділу ромбокубооктаедра площиною по восьмикутному перерізу між двома протилежними паралельними квадратними гранями. Ромбокубооктаедр двома такими розсіченнями може бути розділений на два квадратні куполи та восьмикутну рівносторонню призму.

І навпаки, два чотирисхилих куполи в прямій орієнтації можна поєднати з рівносторонньою восьмикутною призмою по восьмикутній грані, і отримати ромбокубооктаедр (який також можна назвати подовженим квадратним ортобікуполом)

Чотирисхилий купол має вісь поворотної симетрії 4-го порядку, що проходить через центри основ; а також чотири площини дзеркальної симетрії, що проходять через вісь купола та середини сторін нижньої основи.

Шаблон:^

Формули

Діагоналі

Кількість діагоналей опуклого багатогранника: $(\binom{B}{2}) - P$ , де В — кількість вершин, Р — кількість ребер багатогранника. Для чотирисхилого купола:

$(\binom{12}{2}) - 20 = \frac{12}{2} \cdot \frac{11}{1} - 20 = 46$ діагоналей (30 граневих та 16 просторових).

Діагоналі квадратного купола з довжиною ребра $a$
	Граневі діагоналі	$C E = \sqrt{2} \cdot a \approx 1.4142135 \cdot a$ $A B = \sqrt{2 + \sqrt{2}} \cdot a \approx 1.847759 \cdot a$ $A C = (1 + \sqrt{2}) \cdot a \approx 2.4142135 \cdot a$ $A D = \sqrt{4 + 2 \sqrt{2}} \cdot a \approx 2.613125 \cdot a$
	Просторові діагоналі	$A F = \sqrt{2 + \sqrt{2}} \cdot a \approx 1.847759 \cdot a$ $A E = \sqrt{3 + \sqrt{2}} \cdot a \approx 2.1010029 \cdot a$

Метричні характеристики

Для квадратного купола з довжиною ребра $a$ :
Радіус описаної сфери (проходить через всі вершини)	$R = \frac{1}{2} \sqrt{5 + 2 \sqrt{2}} \cdot a$	$\approx 1.39896632 \cdot a$
Радіус напіввписаної сфери (дотикається до всіх ребер)	$ρ = \frac{1}{2} \sqrt{4 + 2 \sqrt{2}} \cdot a$	$\approx 1.30656296 \cdot a$
Вписаної сфери квадратний купол не має
Висота H (Відстань між паралельними квадратною та 8-кутною гранями)	$H = \frac{\sqrt{2}}{2} \cdot a$	$\approx 0.70710678 \cdot a$
Площа поверхні	$S = (7 + 2 \sqrt{2} + \sqrt{3}) \cdot a^{2}$	$\approx 11.5604779 \cdot a^{2}$
Об'єм	$V = (1 + \frac{2 \sqrt{2}}{3}) \cdot a^{3}$	$\approx 1.94280904 \cdot a^{3}$

Центр мас квадратного купола лежить на його осі симетрії на відстані $\frac{5 - 2 \sqrt{2}}{8} \cdot a$ від нижньої основи^[1].

Кути

Плоскі кути граней при вершині: 60°, 90°, 135°.

Кути багатогранника
Двогранний кут між гранями {3} та {4}	$α = \arccos (- \frac{\sqrt{6}}{3})$	≈ 2.5261129 rad ≈ 144°44′ 8.1971′′
Двогранний кут між гранями {3} та {8}	$β = \arccos (\frac{\sqrt{3}}{3})$	≈ 0.9553166 rad ≈ 54°44′ 8.1971′′
Двогранний кут між гранями {4} та {4}	$γ = \arccos (- \frac{\sqrt{2}}{2})$	= $\frac{3 π}{4}$ rad = 135°
Двогранний кут між гранями {4} та {8}	$δ = \arccos (\frac{\sqrt{2}}{2})$	= $\frac{π}{4}$ rad = 45°
Тілесний кут при вершині нижньої основи (восьмикутної)	$Ω_{1} = \frac{π}{4} + \arccos (\frac{2 \sqrt{2}}{3}) = \frac{3 π}{4} - a r c t g (2 \sqrt{2}) =$ $= 4 \arctan (\sqrt{12 - 6 \sqrt{2}} + \sqrt{2} - 3)$	$Ω_{1}$ ≈ 1.125235 ср
Тілесний кут при вершині верхньої основи (квадратної)	$Ω_{2} = 2 π + \arccos (\frac{- 2 \sqrt{2}}{3}) = \frac{3 π}{2} - a r c t g (2 \sqrt{2}) =$ $= \frac{3 π}{4} + 4 \arctan (\sqrt{12 - 6 \sqrt{2}} + \sqrt{2} - 3)$	$Ω_{2}$ ≈ 3.481429 ср
Сферичність	$Ψ = \frac{\sqrt[3]{4 π \cdot (17 + 12 \sqrt{2})}}{7 + 2 \sqrt{2} + \sqrt{3}}$	$Ψ \approx 0.651320998$

Координати вершин

Координати вершин квадратного купола з довжиною ребра a = 1:^[2]

$(\frac{1}{2}, \pm \frac{1}{2}, \frac{\sqrt{2}}{2})$ , $(- \frac{1}{2}, \pm \frac{1}{2}, \frac{\sqrt{2}}{2})$ — ці координати формують верхню квадратну грань купола.
$(\frac{1 + \sqrt{2}}{2}, \pm \frac{1}{2}, 0)$ , $(- \frac{1 + \sqrt{2}}{2}, \pm \frac{1}{2}, 0)$ , $(\frac{1}{2}, \pm \frac{1 + \sqrt{2}}{2}, 0)$ , $(- \frac{1}{2}, \pm \frac{1 + \sqrt{2}}{2}, 0)$ — ці координати формують нижню восьмикутну грань купола, що знаходиться в площині XОY і з центром на початку координат. Вісь купола співпадає з віссю Oz.

Двоїстий багатогранник

Чотирисхилий купол не має канонічно-двоїстого багатогранника (середньовписані сфери обох багатогранників співпадають).

Його топологічно-двоїстий може бути побудований лише загальним чином (кожній грані початкового багатогранника відповідає вершина двоїстого, кожній вершині початкового — грань двоїстого, з дотриманням симетрії початкового багатогранника), а тому форми та розміри двоїстого багатогранника до початкового чотирисхилого купола можуть різнитися.

Двоїстий до чотирисхилого купола (Напіврозсічений чотирикутний трапецоедр, dJ4) має 12 граней: 8 трикутників + 4 дельтоїда; 20 ребер, 10 вершин.

Двоїстий багатогранник	Розгортка двоїстого

Споріднені багатогранники

Чотирисхилий купол належить до родини куполів. Сімейство n-куполів з правильними гранями існує до n = 5 включно.Шаблон:Куполи Два чотирисхилих куполи можуть бути з'єднані своїми восьмикутними основами в прямій орієнтації (поєднуються однойменні бокові грані); отримаємо багатогранник Джонсона J₂₇ — Шаблон:Не перекладено. Якщо один з куполів повернути на 45º, то отримаємо багатогранник Джонсона J₂₉ - Шаблон:Не перекладено.

Також чотирисхилий купол можна з'єднати з восьмикутною призмою, та восьмикутною антипризмою, утворивши при цьому багатогранники Джонсона J₁₉ (Подовжений чотирисхилий купол), та J₂₃ (Скручений подовжений чотирисхилий купол).

Якщо до останніх двох приєднати ще один квадратний купол, отримаємо ромбокубооктаедр, або багатогранники Джонсона — Подовжений чотирисхилий повернутий бікупол (J₃₇), Скручений подовжений чотирисхилий бікупол (J₄₅).


Чотирисхилий прямий бікупол	Чотирисхилий повернутий бікупол	Подовжений чотирисхилий купол	Скручений подовжений чотирисхилий купол	Подовжений чотирисхилий повернутий бікупол	Скручений подовжений чотирисхилий бікупол

Схрещений квадратний купол

Шаблон:Не перекладено — один з неопуклих ізоморфів багатогранників Джонсона, топологічно ідентичний квадратному куполу.

Його можна отримати як зріз Шаблон:Не перекладено або квазіромбокубооктаедра, аналогічно тому, як квадратний купол можна отримати як зріз ромбокубооктаедра. Як і в усіх куполах, багатокутник основи має вдвічі більше ребер і вершин, ніж верхній багатокутник; у цьому випадку багатокутник основи є октаграмою.

Його можна розглядати як купол із ретроградною квадратною основою, побудований, на відміну від квадратного купола, так що квадратні та трикутні грані з’єднують основи, перетинаючись один з одним.

Стільники

Чотирисхилий купол у комбінації з деякими багатогранниками утворює неоднорідні стільники, якими можна заповнити простір.

Заповнити трьохвимірний простір без проміжків та накладень можна за допомогою:^[3]

Квадратних куполів та правильних тетраедрів;
Квадратних куполів, кубів та кубоктаедрів;
Квадратних куполів, квадратних пірамід (J₁), тетраедрів, а також кубом, подовженою квадратною пірамідою (J₈), подовженою квадратною біпірамідою (J₁₅), або їх комбінаціями.

Примітки

Шаблон:Reflist

Література

Шаблон:Стаття (Містить оригінальне перерахування 92 тіл і гіпотезу, що інших немає.)
Шаблон:Книга (Перший доказ, що існує тільки 92 тіл Джонсона.)

Посилання

Шаблон:MathWorld
Polytope Wiki.Square_cupola
McCooey, David.Square Cupola
Klitzing, Richard. "squacu".
Quickfur. "The Square Cupola"

Шаблон:Багатогранники

[1] Шаблон:Cite web

[2] Шаблон:Cite web

[3] Шаблон:Cite web

[1]

[2]

[3]

Чотирисхилий купол

Зміст

Багатогранник Джонсона Шаблон:Math