Правильний додекаедр

Правильний додекаедр
Натисніть тут , щоб подивитися обертання моделі
Тип	Правильний многогранник
Властивості	Опуклий, рівносторонній,однорідний, вершинно-транзитивний, гране-транзитивний
Комбінаторика
Елементи	12 граней ({5}) 30 ребер 20 вершин (3-го степеня)
Грані	12 Правильних п'ятикутників
Характеристика Ейлера	$\chi =\mathrm{\Gamma }-\text{P}+\text{B}=2$
Конфігурація вершини	5.5.5 = 53 В кожній вершині сходяться 3 п'ятикутника.
Вершинна фігура	Правильний трикутник з довжиною сторони $\frac{1+\sqrt{5}}{2}$
Класифікація
Позначення	• D (в Шаблон:Не перекладено ) • D5 (в нотації Стюарта) • U23 (як однорідний многогранник) • C26 (в нотації Г. Коксетера) • W5 (в нотації М. Веннінґера)
Символ Шлефлі	$\{5,3\}$
Шаблон:Не перекладено	3 | 2 5
Діаграма Коксетера-Динкіна	Шаблон:ДКД
Діаграма Шлегеля
Група симетрії	Шаблон:Не перекладено, H3, [5,3], (*532), порядок 120 (Повна ікосаедрична симетрія)
Група обертань	I, [5,3]+, (532), порядок 60
Двоїстий многогранник	Правильний ікосаедр
Розгортка

Правильний додека́едр (від Шаблон:Lang-el — дванадцять і Шаблон:Lang-el — грань) — правильний дванадцятигранник, об'ємна геометрична фігура, поверхня якої складена з дванадцяти правильних п'ятикутників, є одним з п’яти опуклих правильних многогранників (тіл Платона).

Додекаедр складений з 12 правильних п'ятикутних граней.

Має 30 ребер однакової довжини та 20 вершин (у кожній сходяться 3 ребра). Кожна вершина додекаедра є вершиною трьох правильних п'ятикутників.

Його символ Шлефлі — $\{5,3\}$. Це означає, що кожна вершина оточена трьома правильними п'ятикутниками; або також це означає для многогранника, що його грань — , правильний п'ятикутник а вершинна фігура — правильний трикутник . Шаблон:Sfn Шаблон:Rp

Правильний додекаедр має повну Шаблон:Не перекладено I_h, групу Коксетера [5,3], порядку 120, з абстактною структурою групи A₅ × Z₂.

Правильний додекаедр

Правильний додекаедр має 31 вісь обертової симетрії:

‒ 6 осей 5-го порядку ‒ проходять через центри протилежних граней; (поворот на 72°, 144°, 216° і 288° або Шаблон:Ндріб, Шаблон:Ндріб, Шаблон:Ндріб, Шаблон:Ндріб радіан);

‒ 10 осей 3-го порядку ‒ проходять через протилежні вершини; (поворот на 120° і 240° або Шаблон:Ндріб і Шаблон:Ндріб радіан);

‒ 15 осей 2-го порядку ‒ проходять через середини протилежних паралельних ребер (поворот на 180° або Шаблон:Mvar радіан).

Правильний додекаедр має 15 площин дзеркальної симетрії, що проходять через вершину та середину протилежного ребра для кожної грані.

Має центр симетрії (в ньому перетинаються всі осі та площини симетрії).

Сума плоских кутів при кожній з 20 вершин дорівнює 324°.

Правильний додекаедр є третім в нескінченній серії Шаблон:Не перекладено.

Правильний додекаедр має три зірчасті форми.

Геометрія

Куб, вписаний в додекаедр

• Правильний додекаедр з довжиною ребра $a$ можна побудувати, наростивши грані куба з довжиною ребра $\frac{1+\sqrt{5}}{2}\cdot a$ шістьма однаковими клинами певних розмірів таким чином, щоб сусідні трикутні та трапецієподібні грані клинів утворювали правильні п'ятикутники. Шаблон:SfnШаблон:Rp
• У додекаедр можна вписати куб так, що сторони куба будуть діагоналями додекаедра.
• Правильний додекаедр може бути отриманий шляхом зрізання двох осьових вершин п’ятикутного трапецоедра.
• Всі 20 вершин додекаедра лежать по п’ять в чотирьох паралельних площинах, утворюючи в кожній з них правильний п’ятикутник.

Властивості

• Правильний додекаедр має найбільший об’єм серед всіх тіл Платона з тою ж довжиною ребра. Якщо п’ять платонових тіл мають однаковий об’єм, правильний додекаедр має найкоротшу довжину ребра.

• Правильний додекаедр є найокруглішим з п'яти платонових тіл, тобто охоплює найбільший об'єм в межах кулі певного радіусу.

• Перерізом правильного додекаедра площиною, перпендикулярною до осей симетрії 5-го порядку, може бути:
  1. 1. правильний п'ятикутник ; Найбільший за площею переріз у формі правильного п'ятикутника (проходить через п'ять вершин додекаедра паралельно до його грані) ділить висоту додекаедра у співвідношенні Шаблон:Tmath
     2. правильний десятикутник (якщо площина проходить також через центр правильного додекаедра; таких перерізів додекаедр має 6) Шаблон:Rp ;
     3. напівправильний рівнокутний десятикутник (має два типи ребер, що чергуються між собою).

Перерізом правильного додекаедра площиною, що проходить перпендикулярно до осі симетрії 3-го порядку (діагоналі правильного додекаедра) може бути:

1. Правильний трикутник;
2. Правильний шестикутник (якщо площина проходить також через центр правильного додекаедра; таких перерізів додекаедр має 10) Шаблон:Rp ;
3. Напівправильний рівнокутний шестикутник (має два типи ребер, що чергуються між собою).

Анімація складання розгортки додекаедра

• Правильний додекаедр має 43,380 розгорток (так само як і правильний ікосаедр).
  • Для того, щоб зафарбувати правильний додекаедр так, що сусідні грані не матимуть однакового кольору, необхідно принаймні чотири кольори. Кількість способів розфарбувати правильний додекаедр так, щоб всі грані мали різні кольори дорівнює Шаблон:Ндріб = 7 983 360 : група кольорів є групою перестановок з 12 елементів і має розмір 12!, тоді як порядок чистої обертової симетрії правильного додекаедра дорівнює 60 (половина від повної симетрії, тобто 120 елементів).
• Середини двох сусідніх ребер (що мають спільну вершину) та центр додекаедра утворюють рівнобедрений трикутник з внутрішніми кутами 36-72-72, який є «золотим трикутником».

Зв'язок з правильним ікосаедром

Правильний додекаедр та правильний ікосаедр є взаємно двоїстими многогранниками. Тобто центри граней правильного додекаедра є вершинами правильного ікосаедра, і навпаки, центри граней правильного ікосаедра є вершинами правильного додекаедра

Якщо правильний додекаедр має ребро довжиною 1, то його топологічно двоїстий ікосаедр (вершини знаходяться в центрах граней початкового додекаедра) має ребро довжиною $\frac{7+3\sqrt{5}}{10}\approx 1.370820393$, а канонічно двоїстий ікосаедр (напіввписані сфери канонічно-двоїстої пари многогранників збігаються) має ребро довжиною $\phi =\frac{\sqrt{5}+1}{2}\approx 1.618034$.

Серед правильних многогранників як додекаедр, так і ікосаедр являють собою найкраще наближення до сфери. Ікосаедр має найбільше число граней, найбільший двогранний кут і найщільніше притискається до своєї вписаної сфери. З іншого боку, додекаедр має найменший кутовий дефект, найбільший тілесний кут при вершині і максимально заповнює свою описану сферу.

Якщо додекаедр вписано у сферу, то він займає 66.49% об'єму сфери. А ікосаедр, вписаний у ту саму сферу, займає 60.54% її об'єму.

Сфера, що вписана в ікосаедр, охоплює 89,635% його об'єму порівняно з 75,47% для додекаедра.

Об'єм правильного додекаедра з довжиною ребра $a$ більш ніж у три з половиною рази більший за об'єм ікосаедра з такою самою довжиною ребер:

$V_{\text{додек.}}=7.663...\cdot a$ та $V_{\text{ікос.}}=2.181...\cdot a$.

Відношення об'ємів складає:

$\frac{V_{\text{додек.}}}{V_{\text{ікос.}}}=\frac{3(5+3\sqrt{5})}{10}=\frac{3}{5}\cdot (3\phi +1)=1.8\cdot \phi +0.6\approx 3.51246117975$

• В правильний ікосаедр можна вписати правильний додекаедр таким чином, що всі 20 вершин додекаедра знаходитимуться в центрах граней ікосаедра.
• Правильний ікосаедр можна вписати в правильний додекаедр таким чином, що всі 12 вершин ікосаедраа будуть розташовані в центрах 12-ти граней додекаедра.

Зв'язок з «золотим прямокутником»

Шаблон:Multiple image Золоті прямокутники з відношенням сторін (ϕ + 1) : 1 та ϕ : 1 ідеально вписуються в правильний додекаедр.

При цьому дві короткі сторони такого прямокутника збігаються з протилежними паралельними ребрами додекаедра.

Окрім того, центри граней правильного додекаедра (які є вершинами правильного ікосаедра) формують три золоті прямокутники, що перетинаються. [[Файл:|міні]]

Формули

У всіх формулах нижче:

$\phi =2\cdot \cos \left(\frac{\pi }{5}\right)=\frac{\sqrt{5}+1}{2}\approx 1.618034$ — відношення пропорції «золотого перетину».

(Шаблон:OEIS)

$\xi =2\cdot \sin \left(\frac{\pi }{5}\right)=\sqrt{\frac{5-\sqrt{5}}{2}}=\frac{\sqrt[4]{5}}{\sqrt{\phi }}\approx 1.1755705$

Діагоналі

Кількість діагоналей опуклого многогранника: $(\genfrac{}{}{0ex}{}{B}{2})-P$,

де В — кількість вершин, Р — кількість ребер многогранника.

Для правильного додекаедра:

$(\genfrac{}{}{0ex}{}{20}{2})-30=\frac{20}{2}\cdot \frac{19}{1}-30=190-30=160$ діагоналей (60 граневих та 100 просторових).

Діагоналі правильного додекаедра з довжиною ребра $a$
	Граневі діагоналі	$AB=\frac{1+\sqrt{5}}{2}\cdot a=\phi \cdot a$	≈ 1.618033988$\cdot a$
	Просторові діагоналі	$AC=\sqrt{3+\sqrt{5}}\cdot a=\frac{\sqrt{2}+\sqrt{10}}{2}\cdot a=\sqrt{2}\cdot \phi \cdot a$	≈ 2.288245611$\cdot a$
		$AD=\frac{3+\sqrt{5}}{2}\cdot a=(\phi +1)\cdot a$	≈ 2.618033988$\cdot a$
		Найдовша діагональ: $AF=\sqrt{\frac{3(3+\sqrt{5})}{2}}\cdot a=\frac{\sqrt{3}+\sqrt{15}}{2}\cdot a=\sqrt{3}\cdot \phi \cdot a$	≈ 2.802517076$\cdot a$

Метричні характеристики

Для правильного додекаедра з довжиною ребра $a$
Радіус вписаної сфери Шаблон:SfnШаблон:Rp (Торкається всіх граней многогранника)	$r=\frac{1}{2}\cdot \sqrt{\frac{25+11\sqrt{5}}{10}}\cdot a=\frac{2\phi +1}{2\cdot \sqrt{\phi +2}}\cdot a=\frac{\phi +1}{2\cdot \xi }\cdot a$	≈ 1.113516364 $\cdot a$
Радіус напіввписаної сфери Шаблон:SfnШаблон:Rp (Торкається всіх ребер многогранника)	$\rho =\frac{3+\sqrt{5}}{4}\cdot a=\frac{\phi +1}{2}\cdot a$	≈ 1.30901699 $\cdot a$
Радіус описаної сфери Шаблон:SfnШаблон:Rp (Містить всі вершини многогранника)	$R=\frac{1}{2}\cdot \sqrt{\frac{3(3+\sqrt{5})}{2}}\cdot a=\frac{\sqrt{3}+\sqrt{15}}{4}\cdot a=\frac{\sqrt{3}}{2}\cdot \phi \cdot a$	≈ 1.401258538 $\cdot a$
Висота H1 (Відстань між паралельними гранями)	$H_1=2\cdot r=\sqrt{\frac{25+11\sqrt{5}}{10}}\cdot a$	≈ 2.2270327 $\cdot a$
Висота H2 (Відстань між протилежними вершинами)	$H_2=2\cdot R=\frac{\sqrt{3}+\sqrt{15}}{2}\cdot a=\sqrt{3}\cdot \phi \cdot a$	≈ 2.802517077 $\cdot a$
Площа поверхні	$S=3\cdot \sqrt{25+10\sqrt{5}}\cdot a^2=\frac{15\cdot \phi }{\sqrt{3-\phi }}\cdot a^2=15\cdot \frac{\phi }{\xi }\cdot a^2$ $S=30\cdot \sqrt{2\cdot (65-29\sqrt{5})}\cdot r^2$ $S=2\cdot \sqrt{10\cdot (5-\sqrt{5})}\cdot R^2=\frac{20}{\sqrt{2+\phi }}\cdot R^2$	≈ 20.6457288 $\cdot a^2$ ≈ 16.6508731 $\cdot r^2$ ≈ 10.5146222 $\cdot R^2$
Об'єм	$V=\frac{15+7\sqrt{5}}{4}\cdot a^3=\frac{4+7\phi }{2}\cdot a^3$ $V=10\cdot \sqrt{2\cdot (65-29\sqrt{5})}\cdot r^3$ $V=\frac{10\sqrt{3}+2\sqrt{15}}{9}\cdot R^3=\frac{20}{3\cdot \sqrt{3}}\cdot \frac{\phi +1}{\phi +2}\cdot R^3$	≈ 7.66311896 $\cdot a^3$ ≈ 5.55029102 $\cdot r^3$ ≈ 2.78516386 $\cdot R^3$

Відношення радіусів $\frac{R}{r}=\frac{\sqrt{3\cdot (3-\phi )}}{\phi }=\sqrt{15-6\sqrt{5}}\approx 1.25840857$  однакове, як для правильного додекаедра, так і для правильного ікосаедра. Таким чином, якщо правильні додекаедр та ікосаедр мають однакові вписані сфери, то їх описані сфери також рівні між собою. Доведення цього математичного результату дано в Началах Евкліда.

Центр масс правильного додекаедра знаходиться в його геометричному центрі.

Момент інерції суцільного правильного додекаедра з масою Шаблон:Mvar та довжиною ребра Шаблон:Mvar (вісь обертання проходить через центри протилежних граней):

$I=\frac{95+39\cdot \sqrt{5}}{300}\cdot m\cdot a^2\approx 0.6073555037\cdot m\cdot a^2$

Вписана сфера правильного додекаедра	Напіввписана сфера правильного додекаедра	Описана сфера правильного додекаедра

Точка в просторі

Нехай описана сфера додекаедра має радіус R. Нехай дано довільну точку в просторі і відстані від неї до вершин додекаедра дорівнюють d_i . Тоді виконується рівність: Шаблон:Rp

$\frac{1}{20}\sum _{i=1}^{20}{d}_i^4+\frac{16R^4}{9}={(\frac{1}{20}\sum _{i=1}^{20}{d}_i^2+\frac{2R^2}{3})}^2.$

Якщо точка знаходиться на описаній сфері додекаедра, то виконується рівність: Шаблон:Rp

$\sum _{i=1}^{20}{d}_i^2=15\cdot \sum _{i=1}^{20}{d}_i^4$

Кути

Плоскі кути граней при вершині: 108°.

Сума плоских кутів при кожній з 20 вершин дорівнює 324°.

Кути многогранника
Кут, під яким ребро видно з центру правильного додекаедра	$\delta =\arccos \left(\frac{\sqrt{5}}{3}\right)=2\cdot \arcsin \left(\frac{1}{\sqrt{3}\cdot \phi }\right)$	≈ 0.7297276562 rad ≈ 41°48′ 37.1336248′′
Двогранний кут між гранями Шаблон:SfnШаблон:Rp	$\theta =\arccos (-\frac{\sqrt{5}}{5})=2\cdot \arctan \left(\phi \right)=\mathrm{arccot}(-\frac{1}{2})$	≈ 2.0344439358 rad ≈ 116°33′ 54.184237′′
Тілесний кут при вершині	${\mathrm{\Omega }}_1=\arccos (-\frac{11\sqrt{5}}{25})=\arcsin \left(\frac{2\sqrt{5}}{25}\right)=\pi -\arctan \left(\frac{2}{11}\right)$	${\mathrm{\Omega }}_1$ ≈ 2.9617391538 ср
Тілесний кут, під яким грань видно з центра многогранника	${\mathrm{\Omega }}_2=\frac{\pi }{3}$	${\mathrm{\Omega }}_2$ ≈ 1.0471975512 ср
Сферичність	$\mathrm{\Psi }=\frac{\sqrt[3]{\frac{5\pi }{6}\cdot (47+21\sqrt{5})}}{\sqrt{25+10\sqrt{5}}}$	$\mathrm{\Psi }\approx 0.9104531814$

Зауважимо, що $\tan (\pi -\theta )=2$

Координати вершин

Двадцять вершин правильного додекаедра лежать по п'ять у чотирьох паралельних площинах, утворюючи в них чотири правильні п'ятикутники.

Відстані між цими площинами, якщо ребро правильного додекаедра дорівнює 1: Шаблон:SfnШаблон:Rp

$AB=CD=\sqrt{\frac{5+\sqrt{5}}{10}}=\frac{\phi }{\sqrt{\phi +2}}$	≈ 0.850650808352
$BO=OC=\frac{1}{2}\sqrt{\frac{5-\sqrt{5}}{10}}=\frac{1}{2\cdot \sqrt{\phi +2}}$	≈ 0.262865556059
$BC=\frac{AB}{\phi }=\sqrt{\frac{5-\sqrt{5}}{10}}=\frac{1}{\sqrt{\phi +2}}$	≈ 0.525731112119
$AO=OD=\frac{1}{2}\sqrt{\frac{25+11\sqrt{5}}{10}}=\frac{2\phi +1}{2\cdot \sqrt{\phi +2}}$	≈ 1.113516364412
$AC=\sqrt{\frac{5+2\sqrt{5}}{5}}=\frac{\phi +1}{\sqrt{\phi +2}}$	≈ 1.376381920471
$AB=\sqrt{\frac{25+11\sqrt{5}}{10}}=\frac{2\phi +1}{\sqrt{\phi +2}}$	≈ 2.227032728823

Координати вершин правильного додекаедра з довжиною ребра a = 1:

• $(\frac{1}{2}\sqrt{\frac{5+2\sqrt{5}}{5}},\pm \frac{1}{2},\frac{1}{2}\sqrt{\frac{25+11\sqrt{5}}{10}})$, $(-\frac{1}{2}\sqrt{\frac{5-\sqrt{5}}{10}},\pm \frac{1+\sqrt{5}}{4},\frac{1}{2}\sqrt{\frac{25+11\sqrt{5}}{10}})$, $(-\sqrt{\frac{5+\sqrt{5}}{10}},0,\frac{1}{2}\sqrt{\frac{25+11\sqrt{5}}{10}})$;

• $(-\frac{1}{2}\sqrt{\frac{5+2\sqrt{5}}{5}},\pm \frac{1}{2},-\frac{1}{2}\sqrt{\frac{25+11\sqrt{5}}{10}})$, $(\frac{1}{2}\sqrt{\frac{5-\sqrt{5}}{10}},\pm \frac{1+\sqrt{5}}{4},-\frac{1}{2}\sqrt{\frac{25+11\sqrt{5}}{10}})$, $(\sqrt{\frac{5+\sqrt{5}}{10}},0,-\frac{1}{2}\sqrt{\frac{25+11\sqrt{5}}{10}})$;

— ці координати задають вершини верхньої та нижньої п'ятикутних граней, що паралельні до площини Oxy.

• $(\frac{1}{2}\sqrt{\frac{25+11\sqrt{5}}{10}},\pm \frac{1+\sqrt{5}}{4},\frac{1}{2}\sqrt{\frac{5-\sqrt{5}}{10}})$, $(-\frac{1}{2}\sqrt{\frac{5+\sqrt{5}}{10}},\pm \frac{3+\sqrt{5}}{4},\frac{1}{2}\sqrt{\frac{5-\sqrt{5}}{10}})$,$(-\sqrt{\frac{5+2\sqrt{5}}{5}},0,\frac{1}{2}\sqrt{\frac{5-\sqrt{5}}{10}})$ ;
• $(-\frac{1}{2}\sqrt{\frac{25+11\sqrt{5}}{10}},\pm \frac{1+\sqrt{5}}{4},-\frac{1}{2}\sqrt{\frac{5-\sqrt{5}}{10}})$, $(\frac{1}{2}\sqrt{\frac{5+\sqrt{5}}{10}},\pm \frac{3+\sqrt{5}}{4},-\frac{1}{2}\sqrt{\frac{5-\sqrt{5}}{10}})$,$(\sqrt{\frac{5+2\sqrt{5}}{5}},0,-\frac{1}{2}\sqrt{\frac{5-\sqrt{5}}{10}})$ .

— ці координати задають 10 вершин, що лежать в двох паралельних площинах між верхньою та нижньою гранями.

При цьому вісь Oz збігається з однією з осей обертової симетрії 5-го порядку, вісь Oy збігається з однією з осей обертової симетрії 2-го порядку, а площина Oxz є площиною дзеркальної симетрії правильного додекаедра. Центр многогранника знаходиться в початку координат.

Наступні декартові координати визначають 20 вершин правильного додекаедра:

Шаблон:Color box	$(\pm 1,\pm 1,\pm 1)$	Помаранчеві вершини формують куб (пунктирні лінії).
Шаблон:Color box	$(0,\pm \phi ,\pm \frac{1}{\phi })$	Зелені вершини формують «золотий прямокутник» в yz-площині.
Шаблон:Color box	$(\pm \frac{1}{\phi },0,\pm \phi )$	Сині вершини формують «золотий прямокутник» в xz-площині.
Шаблон:Color box	$(\pm \phi ,\pm \frac{1}{\phi },0)$	Рожеві вершини формують «золотий прямокутник» в xy-площині.

де $\phi =\frac{\sqrt{5}+1}{2}\approx 1.618034$ — відношення пропорції «золотого перетину».

Довжина ребра цього додекаедра дорівнює $a=2\cdot (\phi -1)=\frac{2}{\phi }=\sqrt{5}-1$. Центр знаходиться в початку координат. Радіус описаної сфери дорівнює $\sqrt{3}$. При цьому координати (±1, ±1, ±1) є вершинами куба з довжиною ребра b = 2.

Осі координат Ox, Oy та Oz збігаються з осями обертової симетрії 2-го порядку, а координатні площини Oxz, Oyz та Oxy є площинами дзеркальної симетрії правильного додекаедра.

Граф правильного додекаедра

В теорії графів граф правильного додекаедра — це граф з 20 вершинами та 30 ребрами, що має кістяк правильного додекаедра.

Всі 20 вершин графа мають степінь 3, а отже, граф є кубічним.

Спектр графа : $Spec(G)=(-\sqrt{5}{)}^3{(-2)}^4{0}^4{1}^5(\sqrt{5}{)}^3{3}^1$

Цей граф також можна побудувати як узагальнений граф Петерсена G(10,2), де вершини десятикутника з'єднані з вершинами двох п'ятикутників, один п'ятикутник з'єднаний з непарними вершинами десятикутника, а інший п'ятикутник з'єднаний з парними вершинами. Геометрично це можна представити як 10-вершинний екваторіальний пояс додекаедра, з'єднаний з двома 5-вершинними полярними областями, по одній з кожної сторони.

Знаходження гамільтонового циклу для цього графа відомо як гра «Ікосіан», яку в 1859 році запропонував В. Гамільтон. Мета гри — пройти вершинами додекаедра, переходячи від вершини до сусідньої, відвідавши кожну вершину рівно один раз, і при цьому повернувшись у початок (тобто знайти гамільтонів цикл на ребрах додекаедра).

Деякі гамільтонові цикли графа:

Гамільтонів цикл графа додекаедра

{1 – 8 – 9 – 18 – 19 – 11 – 10 – 2 ‒ 3 ‒ 12 – 13 – 20 – 16 – 17 ‒ 7 ‒ 6 – 15 – 14 – 4 ‒ 5 ‒ 1} {1 – 8 – 9 – 18 – 19 – 20 – 16 – 17 ‒ 7 ‒ 6 – 15 – 14 – 13 – 12 ‒ 11 ‒ 10 – 2 – 3 – 4 ‒ 5 ‒ 1} {1 – 2 – 3 – 12 – 13 – 20 – 16 – 17 ‒ 18 ‒ 19 – 11 – 10 – 9 – 8 ‒ 7 ‒ 6 – 15 – 14 – 4 ‒ 5 ‒ 1} {1 – 2 – 10 – 11 – 19 – 18 – 9 – 8 ‒ 7 ‒ 17 – 16 – 20 – 13 – 12 ‒ 3 ‒ 4 – 14 – 15 – 6 ‒ 5 ‒ 1}

Граф правильного додекаедра не має ейлерових циклів.

Реберним графом для графа додекаедра є граф ікосододекаедра. Шаблон:Clear

Ортогональні проєкції

Правильний додекаедр має дві ортогональні проєкції, центровані на вершинах і п'ятикутних гранях, що відповідають площинам Коксетера A₂ та H₂ . Проєкція, центрована по ребру має дві ортогональні лінії відбиття.

Ортогональні проєкції

Центрована по	Вершині	Грані	Ребру
Зображення
Проєктивна симетрія	[[3]] = [6]	[[5]] = [10]	[2]

У перспективній проєкції, якщо дивитися на п'ятикутну грань, правильний додекаедр можна розглядати як діаграму Шлегеля з прямолінійними ребрами, а в стереографічній проекції — як сферичний многогранник. Ці проєкції також використовуються для зображення чотиривимірного 120-комірника, правильного 4-вимірного політопу, побудованого з 120 додекаедрів, при проєктуванні його в 3-вимірний простір.

Проєкція	Ортогональна проєкція	Перспективна проєкція
		Діаграма Шлегеля	Стереографічна проєкція
Правильний додекаедр
Додекаплекс (120-комірник)

Сферичний многогранник

Правильний додекаедр може бути представлений як сферичний многогранник.

Ортографічна проєкція	Стереографічна проєкція

Стільники

Правильними додекаедрами неможливо замостити тривимірний простір без проміжків та накладень.

Замостити тривимірний простір без проміжків та накладень можливо за допомогою правильних додекаедрів , кубів та подвійних серпоротонд у співвідношенні 1: 1: 3.

При цьому власне додекаедри формують реберну ґратку піритоедрів. Подвійні серпоротонди замощують «ромбічні» проміжки. Кожен куб межує з шістьма подвійними серпоротондами в трьох орієнтаціях. Бонні Стюарт позначив цю модель шести подвійних серпоротонд як 6J₉₁(P₄).

Модель стільника

Ґратка додекаедрів

Файл:3D space tessellation of cubes and dodecahedra.ogg 12 серпоротонд навколо додекаедра Анімація заповнення простору

6 подвійних серпоротонд навколо куба

Найбільш щільне пакування додекаедрів (тобто таке, що має найменші пустоти між ними) має щільність $\frac{5+\sqrt{5}}{8}\approx 0.904508497$ . Шаблон:SfnШаблон:Rp

Зірчасті форми

Правильний додекаедр має три зірчасті форми ; всі три є правильними зірчастими многогранниками (тілами Кеплера-Пуансо)

	0	1	2	3
Зірчаста форма	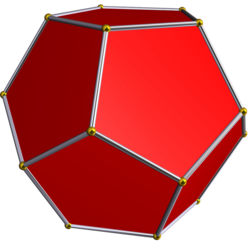Правильний додекаедр	Малий зірчастий додекаедр	Великий додекаедр	Великий зірчастий додекаедр
Діаграмаззірчення та грані на ній

Пов'язані та споріднені многогранники та мозаїки

Шляхом застосування геометричної операції зрізання вершин, правильний додекаедр перетворюється на двоїстий до нього правильний ікосаедр, утворюючи на певних стадіях зрізання такі многогранники:

Правильний додекаедр — Зрізаний додекаедр — Ікосододекаедр — Зрізаний ікосаедр — Правильний ікосаедрШаблон:Ікосаедральні зрізиІкосододекаедр утворюється при застосуванні до правильного додекаедра геометричної операції повне зрізання вершин^[en] (ректифікації). Деякі многогранники Джонсона можна утворити шляхом нарощення граней правильного додекаедра п'ятикутними пірамідами^[en] (J₂):

• Нарощений додекаедр (J₅₈ ) — нарощено одну грань;

• Двічі протилежно нарощений додекаедр (J₅₉) — нарощено дві протилежні грані;

• Двічі косо нарощений додекаедр (J₆₀) — нарощено дві несуміжні, непротилежні грані;

• Тричі нарощений додекаедр (J₆₁) — нарощено три взаємно несуміжні грані.

При застосуванні щодо правильного додекаедра геометричної операції Шаблон:Не перекладено (снубифікація), отримаємо напівправильний многогранник Архімеда — кирпатий додекаедр.

При застосуванні щодо правильного додекаедра геометричної операції Шаблон:Не перекладено (зрізання ребер), отримаємо Шаблон:Не перекладено — Шаблон:Не перекладено.

Кирпатий додекаедр	Шаблон:Не перекладено

Многогранники, що мають розташування вершин як у правильного додекаедра

Шаблон:Не перекладено таке ж, як і в правильного додекаедра, мають чотири неопуклих однорідних многогранників та три Шаблон:Не перекладено.

В правильний додекаедр можливо вписати п'ять різних кубів; їхні ребра є діагоналями граней правильного додекаедра, і всі разом вони утворюють Шаблон:Не перекладено з п'яти кубів. Оскільки два різні тетраедри можуть розміститися на вершинах куба, що чергуються, то в правильний додекаедр також вписується з'єднання п'яти і десяти тетраедрів.

Великий зірчастий додекаедр
	З'єднання п'яти тетраедрів

Прикладом неоднорідного многогранника, що має Шаблон:Не перекладено правильного додекаедра може слугувати Шаблон:Не перекладено — зірчаста форма ромботриаконтаедра.

Тобто правильний додекаедр є опуклою оболонкою вершин цих неопуклих тіл.

Додатково

Будова правильного додекаедра у стереопроєкції.

Шаблон:Не перекладено правильного додекаедра
Просторовими Шаблон:Не перекладено правильного додекаедра є 6 просторових десятикутників.

Приклади в природі

Грані гольмієво-магнієво-цинкового (Ho-Mg-Zn) квазікристалу є правильними п'ятикутниками.

Деякі з правильних та напівправильних тіл зустрічаються у природі у вигляді кристалів, інші — у вигляді вірусів, чи найпростіших мікроорганізмів.

• Кристал піриту ( FeS ) — природна модель додекаедра.

• Вірус поліомієліту має форму додекаедра.

• У 1887 році Ернст Геккель описав радіолярію Circorrhegma dodecahedra, що має форму, наближену до додекаедра

• У 1982 році було синтезовано хімічну сполуку C₂₀H₂₀ (Шаблон:Не перекладено), форма якої також наближена до правильного додекаэдра.

Див. також

• Дванадцятигранник
• Ікосіан
• Напівдодекаедр
• Додекаедричне число
• Шаблон:Не перекладено

Література

• Шаблон:Стаття
• Шаблон:Книга

• Шаблон:Стаття

• Шаблон:Стаття

Посилання

• Шаблон:MathWorld
• Шаблон:Polytope Wiki
• McCooey, David.Dodecahedron
• Klitzing, Richard. "doe".
• Quickfur. "The Dodecahedron"
• Wedd, N. "The Dodecahedron"
• Hi.gher.Space Wiki Contributors. "Dodecahedron"
• Dwunastościan foremny - dodekaedr

• Paper Models of Polyhedra Шаблон:Webarchive
  • Paper Dodecahedron