Плоский модуль

Плоский модуль над кільцем R  — такий модуль, що тензорний добуток на цей модуль зберігає точні послідовності. Модуль називається строго плоским, якщо послідовність тензорних добутків точна тоді і тільки тоді, коли точною є вихідна послідовність.

Векторні простори, вільні і, більш загально, проєктивні модулі є плоскими. Для скінченнопороджених модулів над нетеровим кільцями плоскі модулі  — те ж саме, що проєктивні модулі. Для скінченнопороджених модулів над локальними кільцями все плоскі модулі є вільними модулями.

Поняття плоского модуля було введено Серром в 1955 році.

Означення

Можна дати кілька еквівалентних означень плоского модуля. Нижче означення подані для комутативних кілець.

• (Лівий) $R$-модуль $M$ називається плоским тоді і тільки тоді, коли функтор тензорного добутку $N\mapsto M{\otimes }_{R}N$ є точним. Даний функтор переводить $R$-гомоморфізм $f:N^{\prime }\to N$ у $R$-гомоморфізм $f^{*}:M\otimes N^{\prime }\to M\otimes N,$який на елементах виду $x\otimes y,x\in M,y\in N^{\prime }$ задається як $f^{*}(x\otimes y)=x\otimes f(y)$і лінійно продовжується на весь тензорний добуток.
• Оскільки функтор тензорного добутку завжди є точним справа, попередню вимогу можна послабити. А саме, $R$-модуль $M$ є плоским, якщо для будь-якого ін'єктивного гомоморфізма $R$-модулів $f:K\to L$ індуковане відображення $f^{*}:M{\otimes }_{R}K\to M{\otimes }_{R}L$ також є ін'єктивним.
• Модуль $M$ є плоским, якщо для кожного скінченнопородженого ідеалу в кільці $R$ (з природним вкладенням $I\hookrightarrow R$) індуковане відображення $I{\otimes }_{R}M\to R{\otimes }_{R}M\cong M$є ін'єктивним.
• Існує направлена множина $R$-модулів $\{F_{\alpha }{\}}_{\alpha }$ з такими властивостями:

1. Для всіх $\alpha$, $F_{\alpha }$ є скінченнопородженим вільним $R$-модулем.
2. Індуктивна границя множини рівна $M$: $\underset{\alpha }{\underrightarrow{\lim }}{F}_{\alpha }=M$.

• Для будь-якої лінійної залежності в $M$,

$r^{T}x=\sum _{i=1}^k{r}_i{x}_i=0$,

де $r_i\in R,x_i\in M$, існує матриця $A\in R^{k\times j}$ така що

1. $Ay=x$ має розв'язок для деякого $y\in M^j$.
2. $r^{T}A=0$.

• Для будь-якого $R$-модуля $N$,

${\mathrm{T}\mathrm{o}\mathrm{r}}_1^R(N,M)=0$ де ${\mathrm{T}\mathrm{o}\mathrm{r}}_1^R$ позначає функтор Tor.

• Для будь-якого скінченнопородженого ідеала $I\subset R$,

${\mathrm{T}\mathrm{o}\mathrm{r}}_1^R(R/I,M)=0$.

• Для довільного відображення $f:F\to M$, де $F$ є скінченнопородженим вільним $R$-модулем, і для довільного скінченнопородженого $R$-підмодуля $K\le \ker f$, $f$ розкладається через відображення у вільний $R$-модуль $G,$ для якого образ $K$ є нулем:

Factor property of a flat module

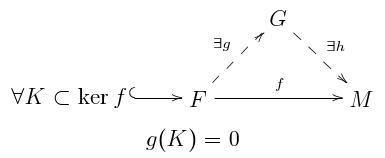
Властивості плоских модулів над комутативним кільцем

• Пряма сума $\underset{i\in I}{⨁}{M}_i$є плоским модулем тоді і тільки тоді, коли кожен модуль $M_i$ є плоским.
• Нехай $\{M_i:i\in I\}$є направленою системою плоских модулів над кільцем R, де I — направлена множина. Тоді індуктивна границя $M=\underrightarrow{\lim }{M}_i$ теж є плоским модулем.
• Теорема Говорова — Лазара: (лівий, правий) модуль M є плоским тоді і тільки тоді, коли він є індуктивною границею скінченнопороджених вільних модулів.
• Для будь-якої мультиплікативної системи S кільця R локалізація кільця S^-1R є плоским R-модулем.
• Модуль M над комутативним кільцем R є плоским тоді і тільки тоді, коли для кожного простого ідеалу $𝔭\subset R$ локалізація $M_{𝔭}$ є плоским ідеалом і тоді і тільки тоді коли для кожного максимального ідеалу $𝔪\subset R$ локалізація $M_{𝔪}$ є плоским ідеалом.
• Скінченнопороджений модуль є плоским тоді і тільки тоді, коли він є локально вільним. Локально вільний модуль над кільцем R  — такий модуль M, що його локалізація за будь-яким простим ідеалом $M_{𝔭}$ є вільним модулем над кільцем часток $R_{𝔭}$.

• Плоскі модулі можна вказати на наступному ланцюжку включень:

Модулі без кручень ⊃ плоскі модулі ⊃ проєктивні модулі ⊃ вільні модулі.

• Для деяких класів кілець правильними є і обернені включення: наприклад, кожен модуль без кручень над дедекіндовим кільцем є плоским, плоский модуль над кільцем Артіна є проєктивним і проєктивний модуль над областю головних ідеалів (або над локальним кільцем) є вільним.
• Якщо M є скінченнопредставленим модулем (тобто існує точна послідовність $0\to K\to F\to M\to 0$ в якій K і F є скінченнопородженими модулями і F також вільним модулем) то M є плоским тоді і тільки тоді, коли він є проєктивним. Якщо додатково R є комутативним локальним кільцем, то M є вільним модулем.
• Для R-модуля еквівалентними M є такі твердження (які можна вважати означеннями строго плоских модулів):
  1. Послідовність $0\to N^{\prime }\stackrel{f}{\to }N\stackrel{g}{\to }{N}^{″}\to 0$ R-модулів є точною тоді і тільки тоді, коли точною є послідовність $0\to M\otimes N^{\prime }\stackrel{f^{*}}{\to }M\otimes N\stackrel{g^{*}}{\to }M\otimes N^{″}\to 0.$
  2. Модуль M є плоским і для довільного R-модуля N, якщо $M\otimes N=0$ то $N=0.$
  3. Модуль M є плоским і для довільного R-гомоморфізма $f:N^{\prime }\to N$, якщо породжений гомоморфізм $f^{*}:M\otimes N^{\prime }\to M\otimes N$є нульовим гомоморфізмом, то і $f=0.$
• Для строго плоского R-модуля M його анулятор $\mathrm{Ann}(M)$є рівним нулю. Натомість плоский модуль із нульовим анулятором не обов'язково буде строго плоским, прикладом чого є $\mathbb{Z}$-модуль $\mathbb{Q}$.
• R-модуль M є строго плоским тоді і тільки тоді, коли він є плоским і для кожного максимального ідеалу $𝔪\subset R,𝔪M\ne M.$
• Якщо кільце S є R-алгеброю, тобто існує гомоморфізм $f:R\to S$, то S є строго плоским R-модулем тоді і тільки тоді, коли кожен простий ідеал кільця R є прообразом під дією f деякого простого ідеалу з S, тобто коли відображення $f^{*}:\mathrm{S}\mathrm{p}\mathrm{e}\mathrm{c}(S)\to \mathrm{S}\mathrm{p}\mathrm{e}\mathrm{c}(R)$ є сюр'єктивним (див. статтю Спектр кільця).
• Нехай, як і вище, S є R-алгеброю і вона є строго плоским R-модулем. Якщо $S{\otimes }_{R}M$ є скінченнопородженим (скінченнопредставленим) S-модулем, то і M є скінченнопородженим (скінченнопредставленим) R-модулем.
• При позначеннях попередньої властивості якщо $S{\otimes }_{R}M$ є скінченнопородженим проєктивним S-модулем, то і M є скінченнопородженим проєктивним R-модулем.

Категорні кограниці

• Прямі суми і індуктивні границі плоских модулів є плоскими. Це випливає з того факту, що тензорний добуток комутує з прямими сумами і індуктивними границями (більше того, воно комутує з усіма кограницями). Підмодулі і фактор-модулі плоского модуля не обов'язково є плоскими (наприклад, плоским не є модуль Z/2 Z). Проте якщо підмодуль плоского модуля є в ньому прямим доданком, то фактор за ним є плоским.

• Модуль є плоским тоді і тільки тоді, коли він є індуктивною границею скінченнопороджених вільних модулів. З цього випливає, зокрема, що кожен скінченнопредставлений плоский модуль є проєктивним.

Приклади

• Оскільки для кільця R і довільного R-модуля M виконується $M\simeq R{\otimes }_{R}M,$то R є плоским R-модулем. Відповідно це ж буде справедливим і для довільного вільного модуля над кільцем R.
• Оскільки $\mathbb{Q}$ є локалізацією кільця $\mathbb{Z}$ за мультиплікативною множиною $\mathbb{Z}\setminus \{0\},$ то $\mathbb{Q}$ є плоским $\mathbb{Z}$-модулем. Це є прикладом плоского але не проєктивного модуля. Також це є прикладом плоского модуля із нульовим анулятором, який не є строго плоским. Дійсно, наприклад, $\mathbb{Q}{\otimes }_{\mathbb{Z}}{\mathbb{Z}}_2=0$але ${\mathbb{Z}}_2\ne 0.$

• Для будь-якого цілого числа $n>1,\mathbb{Z}/n\mathbb{Z}$ не є плоским над $\mathbb{Z},$ оскільки $n:\mathbb{Z}\to \mathbb{Z},x\mapsto nx$ є ін'єктивним, але похідне відображення на тензорному добутку з $\mathbb{Z}/n\mathbb{Z}$ не є ін'єктивним.

• Модуль $\mathbb{Q}/\mathbb{Z}$ не є плоским над $\mathbb{Z}.$

• Для кільця многочленів $S=A[x_1,\dots ,x_r]$ над нетеровим кільцем $A$ і многочлена $f\in S$, що не є дільником нуля, $S/fS$ є плоским над $A$ якщо і тільки якщо $f$ є примітивним многочленом.

• Для нетерового кільця $R$ і його ідеалу $I$ поповнення $A\to \hat{A}$ за ідеалом $I$ є плоским. Воно є строго плоским тоді і тільки тоді, коли $I$ міститься у радикалі Джекобсона кільця $R$.

Гомологічна алгебра

Властивість «плоскості» модуля можна виразити за допомогою функтора Tor, лівого похідного функтора для тензорного добутку. Лівий R- модуль M є плоским тоді і тільки тоді, коли Tor_n^R(-,M) = 0 для всіх $n\ge 1$ (тобто коли Tor_n^R(X, M) = 0 для всіх $n\ge 1$ і всіх правих R-модулів X), означення плоского правого модуля є аналогічним. Використовуючи цей факт, можна довести кілька властивостей короткої точної послідовності модулів:

$0⟶A\stackrel{f}{⟶}B\stackrel{g}{⟶}C⟶0$

• Якщо A і C плоскі, то і B плоский.
• Якщо B і C плоскі, то і A є плоским.

• Якщо A і B плоскі, C в загальному випадку не є плоским. Однак:
• Якщо A  — прямий доданок модуля B і B є плоским, то A і C плоскі.

Плоскі резольвенти

Плоска резольвента модуля M  — це резольвента виду

… → F₂ → F₁ → F₀ → M → 0

де всі F_i є плоскими модулями. Плоскі резольвенти використовуються при обчисленні функтора Tor.

Довжина плоскої резольвенти  — це найменший індекс n, такий що F_n не дорівнює нулю і F_i = 0 для всіх i, що є більшими за n. Якщо модуль M має скінченну плоску резольвенту, її довжина називається плоскою розмірністю модуля. Шаблон:Sfn, в іншому випадку говорять, що плоска розмірність нескінченна. Наприклад, якщо модуль M має плоску розмірність 0, то з точністю послідовності 0 → F₀ → M → 0 випливає, що M є ізоморфним F ₀ , тобто є плоским.

Див. також

• Вільний модуль
• Проєктивний модуль
• Скрут (алгебра)

Література

• Бурбаки Н. Коммутативная алгебра. — М: Мир, 1971.
• Шаблон:Citation
• Шаблон:Citation
• Hideyuki Matsumura, Commutative Ring Theory. Cambridge Studies in Advanced Mathematics, 8. Cambridge University Press, Cambridge, 1986. xiv+320 pp. ISBN 0-521-25916-9