Кубооктаедр

Кубооктаедр
Тип	Багатогранник Архімеда Однорідний багатогранник
Властивості	Напівправильний опуклий, рівносторонній, Шаблон:Не перекладено (тобто і вершинно-транзитивний і реберно-транзитивний)
Комбінаторика
Елементи	14 граней (8{3}+6{4}) 24 ребра 12 вершин (4-го степеня)
Грані	8 Правильних трикутників, 6 Квадратів
Характеристика Ейлера	$\chi =\mathrm{\Gamma }-\text{P}+\text{B}=2$
Конфігурація вершини	3.4.3.4 = [3.4]2 В кожній вершині сходяться 2 трикутника та 2 квадрата.
Вершинна фігура	Прямокутник з довжинами сторін 1 та √2
Класифікація
Позначення	• aC, aaT (в Шаблон:Не перекладено) • U07 (як однорідний багатогранник) • C25 (в нотації Коксетера) • W11 (в нотації Веннінґера)
Символ Шлефлі	r{3,4} або $\left\{\begin{array}{c}3\\ 4\end{array}\right\}$ rr{3,3} або $r\left\{\begin{array}{c}3\\ 3\end{array}\right\}$
	t1{4,3} або t0,2{3,3}
Символ Висофа Шаблон:Iw	Шаблон:Math Шаблон:Math
Діаграма Коксетера-Динкіна	Шаблон:CDD або (o4x3o) Шаблон:CDD
Група симетрії	Oh, B3, [4,3], (*432), порядок 48 (Повна Шаблон:Не перекладено) Td, [3,3], (*332), порядок 24
Група поворотів	O, [4,3]+, (432), порядок 24
Дуальний многогранник	Ромбододекаедр
Розгортка

Кубооктаедр, що обертається

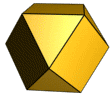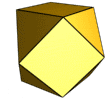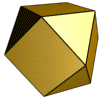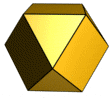
Кубооктаедр — напівправильний опуклий багатогранник, одне з тіл Архімеда, що володіє двома властивостями:

1. Всі грані є правильними багатокутниками (двох типів: правильні трикутники та квадрати);
2. Для будь-якої пари вершин існує симетрія багатогранника (тобто рух, що переводить багатогранник сам в себе), яка переводить одну вершину в іншу.

Складається з 14 граней (8 правильних трикутників та 6 квадратів).

Важливою ознакою багатогранника є те, що він має тільки два типи граней, причому кожна грань одного типу сусідня тільки з гранями іншого типу, тобто грані чергуються навколо кожної вершини. Ці багатогранники реберно-транзитивні, тому на крок ближче до правильних багатогранників, ніж напівправильні, які лише вершинно-транзитивні. Багатогранники, що мають цю властивість, називаються квазіправильними. Існує ще тільки один опуклий квазіправильний багатогранник — ікосододекаедр.

В кубооктаедрі 12 однакових вершин, в яких сходяться два трикутники і два квадрати, а також 24 однакових ребра, кожне з яких розділяє між собою трикутну і квадратну грані.

Двоїстий до кубооктаедра многогранник — ромбододекаедр.

Графічне зображення

Кубооктаедр можна отримати з куба або октаедра, застосувавши до них геометричну операцію «Шаблон:Не перекладено» ‒ процес зрізання багатогранника шляхом позначки середини всіх його ребер і відсічення всіх вершин аж до цих точок.

Наступна послідовність многогранників ілюструє утворення кубооктаедра:

Шаблон:Center

Шаблон:Center

Шаблон:Center

Кубооктаедр з ребром $a$ є спільною частиною поєднанняя куба з ребром $\sqrt{2}\cdot a$ та октаедра з ребром $2\cdot a$. При цьому кубооктаедр займає $\frac{5}{6}$ об'єму, що займає куб та $\frac{5}{8}$ об'єму, що займає октаедр.

Кубооктаедр можна розділити площиною на дві рівні частини. При цьому переріз матиме форму правильного шестикутника. Таких шестикутних перерізів кубооктаедр має чотири. При цьому утворюються два трисхилих купола — багатогранник Джонсона J3, повернені відносно один одного. Тому кубооктаедр також можна назвати скрученим трисхилим бікуполом.

При іншому екваторіальному перерізі кубооктаедра утворюється квадрат.

Ще одна Розгортка кубооктаедра

Файл:Cuboctahedron.stl

Формули

Діагоналі

Кількість діагоналей опуклого багатогранника: $(\genfrac{}{}{0ex}{}{B}{2})-P$, де В — кількість вершин, Р — кількість ребер багатогранника. Для кубооктаедра:

$(\genfrac{}{}{0ex}{}{12}{2})-24=\frac{12}{2}\cdot \frac{11}{1}-24=42$ діагоналі (12 граневих та 30 просторових).

Діагоналі кубооктаедра з довжиною ребра $a$
	Гранева діагональ	$AB=\sqrt{2}\cdot a\approx 1.41421356237\cdot a$
	Просторові діагоналі	$AC=\sqrt{3}\cdot a\approx 1.73205080756\cdot a$ $AD=2\cdot a$

Метричні характеристики

Для кубооктаедра з довжиною ребра а:
Радіус описаної сфери (проходить через всі вершини)		$R=a$
Радіус напіввписаної сфери (дотикається до всіх ребер)		$\rho =\frac{\sqrt{3}}{2}\cdot a$	$\approx 0.8660254\cdot a$
Радіус сфери r3 та r4 (дотична до всіх трикутних граней та відповідно, квадратних граней в їх центрах)	Вписаної сфери кубооктаедр не має	$r_3=\frac{\sqrt{6}}{3}\cdot a$	$\approx 0.8164965\cdot a$
		$r_4=\frac{\sqrt{2}}{2}\cdot a$	$\approx 0.7071067\cdot a$
Висота H3 та H4 (Відстань між протилежними трикутними та протилежними квадратними гранями)		$H_3=2\cdot \frac{\sqrt{6}}{3}\cdot a$	$\approx 1.6329931\cdot a$
		$H_4=\sqrt{2}\cdot a$	$\approx 1.4142135\cdot a$
Площа поверхні		$S=2\cdot (3+\sqrt{3})\cdot a^2$	$\approx 9.4641016\cdot a^2$
Об'єм		$V=\frac{5}{3}\sqrt{2}\cdot a^3$	$\approx 2.3570226\cdot a^3$

Кути

Плоскі кути граней при вершині: 60°, 90°.

Сума плоских кутів при кожній вершині дорівнює 300°.

Кути багатогранника
Кут між несусідніми ребрами при вершині	$\phi =\arccos (-\frac{1}{2})$	$=\frac{2\pi }{3}$ rad = 120°
Кут, під яким ребро кубооктаедра видно з його центра	$\theta =\arccos \left(\frac{1}{2}\right)$	$=\frac{\pi }{3}$ rad = 60°
Двогранний кут між гранями {3} та {4}	$\alpha =\arccos (-\frac{\sqrt{3}}{3})=\mathrm{arcsec}(-\sqrt{3})$	≈ 2.18627603546528 rad ≈ 125° 15′ 51.80285791′′
Тілесний кут при вершині	$\mathrm{\Omega }=\arccos (-\frac{7}{9})=4\arcsin \left(\frac{\sqrt{3}}{3}\right)=$ $=8\arctan (\sqrt{3}-\sqrt{2})$	$\mathrm{\Omega }\approx 2.4619188346815$ ср $\approx 0.7837\pi$ ср
Тілесний кут, під якимм трикутну грань видно з центру кубооктаедра	${\mathrm{\Omega }}_1=2\pi -6\cdot \arcsin \left(\frac{\sqrt{6}}{3}\right)$	${\mathrm{\Omega }}_1\approx 0.551285598432$ ср
Тілесний кут, під якимм квадратну грань видно з центру кубооктаедра	${\mathrm{\Omega }}_2=2\pi -8\cdot \arcsin \left(\frac{\sqrt{3}}{3}\right)$	${\mathrm{\Omega }}_2\approx 1.359347637816$ ср
Сферичність	$\mathrm{\Psi }=\sqrt[3]{\frac{25\pi (9-5\sqrt{2})}{36}}$	$\mathrm{\Psi }\approx 0,90499718$

Зірчасті форми кубооктаедра

Продовження граней кубооктаедра призводить до чотирьох зірчастих багатогранників:

• 
  Кубооктаедр
• 
  Перша зірчаста форма
• 
  Друга зірчаста форма
• 
  Третя зірчаста форма
• 
  Четверта зірчаста форма

Грані зірчастих форм кубооктаедра

• 
  Кубооктаедр
• 
  Перша зірчаста форма
• 
  Друга зірчаста форма
• 
  Третя зірчаста форма
• 
  Четверта зірчаста форма

Перша зірчаста форма виходить шляхом добудови на гранях кубооктаедра трикутних та чотирикутних пірамід і є сполукою куба та октаедра.

Наступна зірчаста форма утворена шляхом приєднання 24 біпірамід до сполуки куба та октаедра.

Третя зірчаста форма кубооктаедра є поєднанням шести прямих квадратних пірамід.

Остання зірчаста форма кубооктаедра є поєднанням зірки Кеплера (зірчастого октаедра) і трьох правильних чотирикутних призм, загальною частиною яких є вихідний куб.

Ортогональні проєкції

Кубооктаедр має чотири спеціальних ортогональних проєкцій, що центровані по вершині, ребру та двох типах граней (трикутній та квадратній). Дві останні відповідають площинам Кокстера BШаблон:Sub і AШаблон:Sub. Косі проекції показують квадрат і шестикутник, що проходять через центр кубоктаедра.

Ортогональні проєкції кубооктаедра

Центровані по	Вершині	Ребру	Трикутній грані	Квадратній грані	Косі проєкції
Зображення
Проєктивна симетрія	[2]	[2]	[6]	[4]
Ромбододекаедр (Двоїстий багатогранник)
Зображення

Граф кубооктаедра

Шаблон:Граф В теорії графів граф кубооктаедра — це один з архімедових графів, що має кістяк кубооктаедра.

Він має 12 вершин степеня 4 і 24 ребра.

Граф кубооктаедра — планарний локально лінійний граф, який можна утворити як реберний граф куба або приклеюванням антипризм у внутрішню та зовнішню грані 4-циклу. Також він є Шаблон:Не перекладено та симетричним графом.

Граф кубооктаедра є цілим графом та має спектр $Spec(G)=(-2{)}^5{0}^3{2}^3{4}^1$

Має 200 гамільтонових циклів. Деякі з них:

Гамільтонів цикл графа кубооктаедра

{1 — 2 — 3 — 4 — 8 — 9 — 5 — 10 — 6 — 11 — 12 — 7 — 1}

{1 — 2 — 3 — 4 — 5 — 9 — 10 — 6 — 11 — 7 — 12 ‒ 8 — 1}

{1 — 2 — 3 — 4 — 5 — 10 — 6 — 11 — 7 — 12 — 9 ‒ 8 — 1}

Цікаві відомості

Заповнення простору

Кубооктаедрами неможливо заповнити тривимірний простір без проміжків та накладень, тому що при змиканні квадратів залишається незайнятим простір у вигляді октаедра, а при змиканні трикутників — у вигляді кубів. Заповнити тривимірний простір без проміжків і накладень можна за допомогою кубооктаедрів та інших багатогранників, наприклад, октаедрів чи кубів.

• 
  Кубооктаедр + Октаедр
• 
  Кубооктаедр + Ромбокубоктаедр + Куб
• 
  Кубооктаедр + Зрізаний октаедр + Зрізаний тетраедр

Кубоктаедр можна отримати, взявши екваторіальний переріз чотиривимірних 24-комірника або 16-комірника.

Правильний ікосаедр топологічно ідентичний кубооктаедру з 6 квадратними гранями, розбитими по діагоналях.

Двоїстий багатогранник

Кубооктаедр має канонічно-двоїстий багатогранник. Середньовписані сфери канонічно двоїстої пари багатогранників співпадають. Для такого способу побудови — двоїстий багатогранник до двоїстого співпадає з початковим. Грань двоїстого будується методом Дормана Люка (метод діє лише для однорідних багатогранників).

Канонічно двоїстим багатогранником до кубооктаедра є Ромбододекаедр.

Має 12 граней: ромби з гострим кутом $\alpha =\arccos \left(\frac{1}{3}\right)\approx 1.2309594rad\approx 70^{\circ }31^{\prime }43.6057^{″}$ ; 24 ребер, 14 вершин.

Якщо ребро кубооктаедра дорівнює $a$, то ребро двоїстого ромбододекаедра дорівнює $\frac{3\sqrt{6}}{8}\cdot a\approx 0.91855\cdot a$

• 
  Ромбододекаедр
• 
  Розгортка ромбододекаедра
• 
  Поєднання кубооктаедра та ромбододекаедра

Споріднені багатогранники

Кубооктаедр належить до родини однорідних многогранників, пов'язаних з кубом та октаедром.

Кубоктаедр має повну Шаблон:Не перекладено O_h, порядок 48. В цьому випадку його можна розглядати як Шаблон:Не перекладено октаедр або повністю зрізаний куб. Шаблон:Октаедричні зрізи

Кубоктаедр також має тетраедричну симетрію T_d, порядок 24 з двома кольорами трикутників. Його можна розглядати як Шаблон:Не перекладено тетраедр і можна назвати ромботетратетраедром:

Кубоктаедр також має симетрію D_3d, порядок 12. В цьому випадку його можна розглядати як трисхилий повернутий бікупол.

Джерела

• Шаблон:MathWorld
• Пчелінцев В. О. Кристалографія, кристалохімія та мінералогія. Навчальний посібник для студентів вищих навчальних закладів. Суми: Вид-во СумДУ, 2008, — 232с.
• Гордєєва Є. П., Величко В. Л. Нарисна геометрія. Багатогранники (правильні, напівправильні та зірчасті). Частина І. Навчальний посібник. Луцьк: Редакційно-видавничий відділ ЛДТУ, 2007, — 198с. Шаблон:Webarchive
• П. С. Александрова, А. И. Маркушевича и А. Я. Хинчина. Многоугольники и многогранники. Энциклопедия элементарной математики. Москва: Государственное издательство физико-математической литературы, 1963, — 568с.