Локон Аньєзі

Локон Аньєзі (також верзієра Аньєзі , кубіка Аньєзі, дзвоноподібна крива Коші ^[1]) — плоска алгебрична раціональна крива третього порядку, що визначається двома діаметрально протилежними точками кола. Шаблон:Clear

Анімація, що ілюструє утворення локона Аньєзі

Означення

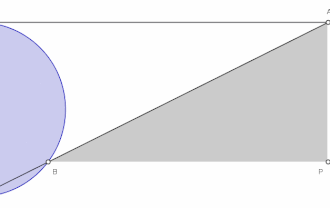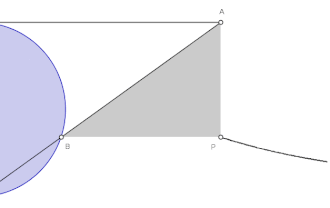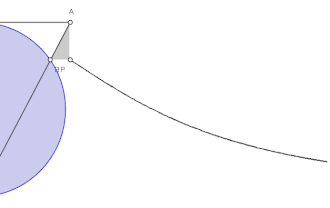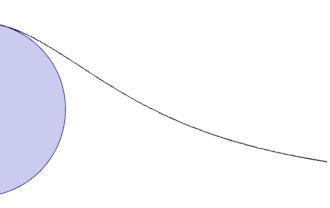
Нехай дано коло діаметром $O A$ з опорною точкою $O = (0; 0)$ в початку координат. Січна $O L$ (дотична до кола $A L ∥ O x$ ) перетинає це коло в точці $C$ . Проведено прямі $C M ⊥ O A$ та $L M ∥ O A$ . Геометричне місце точок $M$ перетину цих прямих є локоном Аньєзі.Шаблон:Sfn Шаблон:Rp

Також, локон Аньєзі Шаблон:Sfn Шаблон:Rp Шаблон:Sfn Шаблон:Rp — геометричне місце точок $M$ , для яких виконується співвідношення $\frac{B M}{B C} = \frac{O A}{O B}$

де $O A$ — діаметр кола;
$B C$ — напівхорда цього кола, перпендикулярна до $O A$ .

Свою назву "локон Аньєзі" крива отримала на честь італійської математикині Марії Гаетани Аньєзі, яка досліджувала цю криву.

Лінія четвертого порядку, що складається з локона Аньєзі та прямої, що збігається з віссю абсцис, є одним з випадків кривих, під назвою яйце Гренвіля

Рівняння

Нехай твірне коло локона Аньєзі має точку опори $O = (0, 0)$ , в початку координат. Діаметрально протилежна точка кола $A = (0, a)$ лежить на осі $O y$ , тобто діаметр твірного кола дорівнює $O A = a$ .
Тоді локон Аньєзі має наступні рівняння:

У декартовій системі координат:

y = \frac{a^{3}}{a^{2} + x^{2}}

.

або ж:

x^{2} y = a^{2} \cdot (a - y)

.

Шаблон:Hider

При $a = 1$ рівняння кривої матиме вигляд:

y = \frac{1}{1 + x^{2}}

.

Ця крива є графіком похідної функції арктангенса. ^[2]

Параметричне рівняння в декартовій системі координат Шаблон:Sfn Шаблон:Rp:

{\begin{matrix} x (φ) = a \cdot tg φ \\ y (φ) = a \cdot \cos^{2} φ \end{matrix} - \frac{π}{2} < φ < \frac{π}{2}

,

де параметр $φ = ∠ A O C$ — кут між $O A$ і $O C$ ; точці $A$ відповідає значення $φ = 0$ .

Шаблон:Hider

Раціональна параметризація для кривої має вигляд:

{\begin{matrix} x (t) = a \cdot t \\ y (t) = \frac{a}{1 + t^{2}} \end{matrix}; - \infty < t < + \infty

;

У полярній системі координат рівняння локону досить складне; щоб його знайти, треба розв'язати кубічне рівняння:

ρ \sin φ = \frac{a^{3}}{a^{2} + ρ^{2} \cos^{2} φ}

ρ^{3} (\cos^{2} φ \sin φ) + ρ (a^{2} \sin φ) - a^{3} = 0

Однак отримана формула буде занадто складною і невкладистою, щоб мати якесь практичне значення.

Властивості

Локон Аньєзі — алгебрична раціональна крива третього порядку.

Згідно класифікації Ньютона кривих третього порядку, локон Аньєзі є гіперболізмом кола та має нескінченно віддалену ізольовану точку на осі $O y$ .Шаблон:Sfn Шаблон:Rp

Діаметр $O A$ єдина вісь симетрії кривої. Вісь $O x$ (дотична до твірного кола в його точці опори) — асимптота локона Аньєзі.
Крива має один максимум — $A (0; a)$ і дві точки перегину, що відповідають параметричним кутам $φ = \pm \frac{π}{6}$ та мають координати : $P_{1} (- \frac{a}{\sqrt{3}}; \frac{3 a}{4})$ та $P_{2} (\frac{a}{\sqrt{3}}; \frac{3 a}{4})$ . ^[3] ^[4] Шаблон:Rp

Точки перегину лежать на прямих $y = \pm \frac{3 \sqrt{3}}{4} \cdot x$

Кути $α_{1}$ та $α_{2}$ між дотичними в точках перегину $P_{1}$ та $P_{2}$ та додатнім напрямом осі $O x$ можна визначити за формулами:

tg α_{1, 2} = \mp \frac{3 \sqrt{3}}{8}

Для побудови дотичних $P_{1} F$ та $P_{2} F$ достатньо відкласти відрізок $A F = \frac{a}{8}$ на продовженні діаметра $O A$ (у випадку представлених вище рівнянь кривої — точка $F$ знаходиться на осі $O y$ та має координати $F = (0; a + \frac{a}{8})$ ).

В околі вершини $A$ локон наближається до кола діаметром $O A$ . У точці $A$ відбувається дотик, і крива збігається з колом. Це показує значення радіуса кривини в точці $A$ : $R_{A} = \frac{a}{2}$ .

Центр кривини кривої в точці $A$ збігається з центром твірного кола.

Площа під графіком (між кривою і асимптотою): $S = π a^{2}$ . ^[3] ^[4] Шаблон:Rp ^[5]

Вона обчислюється інтегруванням рівняння по всій числовій прямій $ℝ$ ^[6], і дорівнює площі визначального круга, помноженій на 4.

Центр мас фігури, що обмежена кривою та її асимптотою лежить на осі симетріі, на відстані $\frac{a}{4}$ від асимптоти, . (у випадку представлених вище рівнянь кривої — центр мас знаходиться на осі $O y$ та має координати $(0; \frac{a}{4})$ ).^[4] Шаблон:Rp

Найбільший за площею прямокутник, який можна вписати між кривою та її асимптотою, має висоту, що дорівнює радіусу визначального кола, і ширину, що дорівнює подвоєному діаметру кола. Його площа: $S = a^{2}$ . ^[5]
Об'єм тіла, утвореного обертанням кривої навколо своєї асимптоти (осі $O x$ ): $V = \frac{π^{2}}{2} \cdot a^{3}$ .^[3] ^[4] Шаблон:Rp .

Цей об'єм вдвічі більший за об'єм тора, утвореного при обертанні визначального кола локона Аньєзі навколо цієї ж прямої.^[5]
Об'єм тіла, утвореного при обертанні локона Аньєзі навколо осі симетрії (в нашому випадку навколо осі $O y$ ) має нескінченне значення.Шаблон:Sfn Шаблон:Rp

Побудова

Шаблон:Multiple image

Будуємо коло діаметром $O A = a$ і через нижню точку кола О проводимо дотичну Ox.
Через верхню точку кола A (діаметрально протилежну до О) проводимо пряму, паралельну до Ох.
Через точку О проводимо січну ОL, яка перетинає коло в точці C і верхню пряму в точці L.
Через точку C проводимо пряму, паралельну до Ох, а через L проводимо пряму, паралельну до діаметра ОA. Ці дві прямі перетинаються в точці M, яка належить локону Аньєзі.

Споріднені криві та деякі узагальнення

Коли точка $M$ окреслює локон Аньєзі (див. означення локона Аньєзі вище), то точка, що знаходиться в середині відрізка $C L$ окреслить криву

(2 y - a) \cdot (x^{2} + y^{2}) = a \cdot y^{2}

.

Цю криву називають візієрою Пеано або супровідною цисоїдиШаблон:Sfn Шаблон:Rp

Параметричні рівняння цієї кривої:

{\begin{matrix} x (t) = \frac{a \cdot t \cdot (t^{2} + 2)}{2 (t^{2} + 1)} \\ y (t) = \frac{a \cdot (t^{2} + 2)}{2 (t^{2} + 1)} \end{matrix}; - \infty < t < + \infty

.

де $O A = a$ — діаметр твірного кола локона Аньєзі (також і візієри Пеано); ' Візієра має ізольовану точку $O = (0; 0)$ та асимптоту $y = \frac{a}{2}$

Візієра має один максимум в точці $A = (0; a)$ та дві точки перегину, що мають координати : $Q_{1, 2} = (\pm \frac{4 a}{5} \cdot \sqrt{\frac{2}{3}}; \frac{4 a}{5})$ .

Площа, що міститься між візієрою та її асимптотою дорівнює $S = 5 π a^{2}$ .

Побудова Шаблон:Sfn Шаблон:Rp
Пряма $ℓ$ , що проходить через початок координат, перетинає коло $x^{2} + y^{2} = 2 r \cdot y$ в точці $E$ , а пряму $y = 2 r$ — в точці $F$ . Через проєкцію $C$ точки $F$ на вісь $O x$ проведено пряму, що паралельна до $ℓ$ .
Точка $P$ її перетину з перпендикуляром із $E$ на $O y$ належить візієрі

x^{2} \cdot y = (2 r + y)^{2} \cdot (2 r - y)

.

В колі $K$ з центром $C$ та радіусом $r$ проведено хорду $O B$ . Кут між $C O$ та $O B$ дорівнює $α$ . Змінна пряма $ℓ$ , що проведена через $O$ , перетинає коло в точці $D$ , і в точці $E$ дотичну до кола в його точці $B$ . На прямій $ℓ$ відкладаємо відрізок $E P$ , що дорівнює $O D$ ( в тому ж напрямі).

Точка $P$ окреслює криву

(x^{2} + y^{2}) \cdot (x \cdot \cos α + y \cdot \sin α - 4 r \cdot \cos^{2} α) + 2 r \cdot y^{2} = 0

,

яку називають косою візієрою (за вісь $O x$ прийнято пряму $O B$ ; початок координат знаходиться в точці $O$ ).

Подвійна точка $O$ є або вузловою, або точкою звороту, або ізольованою, в залежності від співвідношення $α ⋚ \frac{π}{4}$ .

Особливий фокус кривої знаходиться в центрі кола $K$ . А окремому випадку, при $α = \frac{π}{4}$ , крива є цисоїдою.Шаблон:Sfn Шаблон:Rp

Псевдоверзієра (також псевдо-локон) .Шаблон:Sfn Шаблон:Rp

Шаблон:Sfn Шаблон:Rp Шаблон:Sfn Шаблон:Rp — крива, що утворюється шляхом подвоєння ординат локона Аньєзі.

Означення Нехай з точки $D = (0; 2 a)$ проведено перпендикуляр $D N$ на змінну пряму $O L = ℓ$ (точка $O = (0; 0)$ — початок координат).
З точки $N$ їх перетину проведено пряму $N M ∥ O x$ , що перетинає вісь $O y$ в точці $E$ . Із точки $L$ перетину прямих $O L = ℓ$ та $A L (y = a)$ проведено пряму $L M ∥ O y$ . Геометричне місце точок $M$ перетину прямих $N M$ та $L M$ є псевдоверзієрою.
Її рівняння у декартовій системі координат Шаблон:Sfn Шаблон:Rp:

y = \frac{2 a^{3}}{a^{2} + x^{2}}

.

або ж:

x^{2} y = a^{2} \cdot (2 a - y)

.

Цю криву досліджував Дж. Грегорі в 1658 і використовував Готфрід Лейбніц у 1674 році, виводячи вираз: ^[4] Шаблон:Rp

\frac{π}{4} = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + . . .

Узагальненням локона Аньєзі можуть бути криві:
- Аньєзіана Шаблон:Sfn Шаблон:Rp — пряма $A L$ (див. означення локона Аньєзі) займає довільне положення, та перпендикулярна до $O A$ .

Означення Пряма $ℓ$ , що проходить через початок координат $O = (0; 0)$ , перетинає коло $x^{2} + y^{2} = a \cdot y$ та пряму $y = b$ в точках $C$ та $L$ відповідно. Точка $M$ перетину прямих $C M$ та $L M$ , що паралельні до осей координат $O x$ та $O y$ відповідно, окреслює криву