Квадратурно-амплітудна модуляція

Шаблон:Методи модуляції Квадратурно-ампліту́дна модуляція (КАМ) (Шаблон:Lang-en) — різновид амплітудної модуляції сигналу, яка є сумою двох несучих коливань однієї частоти, але зміщених за фазою один відносно одного на 90°, кожне з яких промодулюване по амплітуді своїм модулюючим сигналом:

$\begin{array}{cc}s(t)& =I(t)\cos (2\pi f_{0}t)-Q(t)\sin (2\pi f_{0}t)\end{array}$

де $I(t)$ та $Q(t)$ — модулюючі сигнали, $f_0$ — частота-носій.

Квадратурно-амплітудну модуляцію використовують як в цифрових так і аналогових схемах модуляції. В ній передається два аналогових сигнали повідомлення, або два цифрові потоки біт, за допомогою зміни (модуляції) амплітуд двох сигналів-носіїв, з використанням амплітудної маніпуляції як схеми цифрової модуляції або амплітудної модуляції (АМ) для аналогової схеми модуляції.

КАМ використовують в оптоволоконних системах для збільшення швидкості передачі даних; КАМ16 і КАМ64 можна оптично змоделювати за допомогою 3-крокового інтерферометра.

Введення

Як і всі схеми модуляції, КАМ передає дані змінюючи деякі аспекти сигналу носія, або опорної хвилі, (зазвичай синусоїди) відповідно до сигналу даних. У випадку КАМ, змінюється (модулюється) амплітуда двох хвиль, що відрізняються на 90° по фазі одна від одної (в квадратурі) для того, щоб представити сигнал. Амплітудна модуляції двох носіїв в квадратурі можна еквівалентно розглядати як модуляцію обох: фази і амплітуди одного носія.

Фазова модуляція (аналогова ФМ) і фазова маніпуляція (цифрова ФМ) можуть розглядатися як особливий різновид КАМ, в якій магнітуда модульованого сигналу не змінюється, і лише фаза змінюється.

Аналогова КАМ

Аналогова КАМ: заміряного кольорового сигналу PAL на екрані векторного аналізатору.

При передачі двох сигналів, модульованих за допомогою КАМ, сигнал що передається буде мати форму:

$\begin{array}{cc}s(t)& =\mathrm{\Re }\left\{[I(t)+iQ(t)]e^{i2\pi f_{0}t}\right\}\\ & =I(t)\cos (2\pi f_{0}t)-Q(t)\sin (2\pi f_{0}t)\end{array}$

де $i^2=-1$, $I(t)$ і $Q(t)$ модулюючі сигнали, $f_0$ частота-носій і $\mathrm{\Re }\{\}$ — дійсна частина.

Приймачем, ці два модульовані сигнали можуть бути демодульовані з використанням когерентного демодулятору. Такий приймач помножує отриманий сигнал окремо із косинусним і синусним сигналом, щоб отримати прийняті оцінки для $I(t)$ і $Q(t)$ відповідно. Завдяки властивості ортогональності опорних сигналів, модульовані сигнали можна виявити незалежно один від одного.

В ідеальному випадку $I(t)$ зворотня модулюється виконується за допомогою множення сигналу що передається із косинусним сигналом:

$\begin{array}{cc}r(t)& =s(t)\cos (2\pi f_{0}t)\\ & =I(t)\cos (2\pi f_{0}t)\cos (2\pi f_{0}t)-Q(t)\sin (2\pi f_{0}t)\cos (2\pi f_{0}t)\end{array}$

Використовуючи стандартні тригонометричні тотожності, ми можемо записати це як:

$\begin{array}{cc}r(t)& =\frac{1}{2}I(t)[1+\cos (4\pi f_{0}t)]-\frac{1}{2}Q(t)\sin (4\pi f_{0}t)\\ & =\frac{1}{2}I(t)+\frac{1}{2}[I(t)\cos (4\pi f_{0}t)-Q(t)\sin (4\pi f_{0}t)]\end{array}$

Фільтр низьких частот $r(t)$ усуває високочастотні складові (що містять в собі $4\pi f_{0}t$), залишаючи лише складову $I(t)$. Цей фільтрований сигнал не залежить від $Q(t)$, що показує, що синфазна складова може бути отримана незалежно квадратурної складової. Так само ми можемо помножити $s(t)$ на синусну хвилю і потім пропустити через фільтр низьких частот $Q(t)$.

Аналогова КАМ має ті самі недоліки, що і односмугова модуляція: точна фаза носія потрібна аби правильно демодулювати сигнал на приймачі. Якщо демодулююча фаза хоча б трохи інша, це призведе до появи перехресних завад між модульованими сигналами. В КАМ системах потрібно вирішувати якимось чином цю задачу синхронізації носія на приймачі. Когерентний демодулятор повинен бути точно у фазі з отриманим сигналом, інакше модульовані сигнали не можна отримати незалежно. Зазвичай це досягається передачею імпульсного субносія або пілот-сигналу.

Аналогова КАМ використовується в:

• Аналогових системах кольорового телебачення NTSC і PAL, де I- та Q-сигнали передають компоненти хрому (колір) інформації. КАМ фаза-носій відновлюється відновлюється із спеціального сигналу кольорової синхронізації, що передається на початку кожного рядка розгортки.
• C-QUAM («Сумісна КАМ, Шаблон:Lang-en») використовується в AM стерео радіо для передачі різниці стерео інформації.

Аналіз Фур'є для КАМ

В частотній області, КАМ має схоже спектральне представлення до модуляції DSB-SC. Використовуючи властивості перетворення Фур'є, можна отримати наступне:

$S(f)=\frac{1}{2}[M_I(f-f_0)+M_I(f+f_0)]+\frac{i}{2}[M_Q(f-f_0)-M_Q(f+f_0)]$

де S(f), M_I(f) і M_Q(f) це перетворення Фур'є (представлення в частотній області) сигналів s(t), I(t) і Q(t), відповідно.

Квантована КАМ

Цифрова 16-КАМ з прикладом точок сузір'я

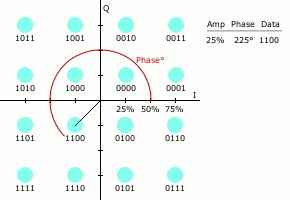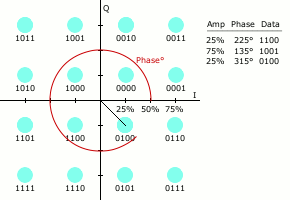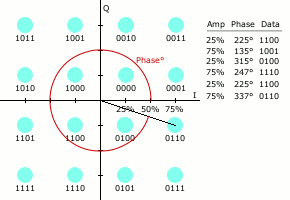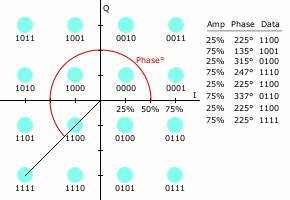
Як і в багатьох схемах цифрової модуляції, для КАМ можна побудувати діаграму сигнального сузір'я. В КАМ точки сузір'я, як правило, розташовуються у вигляді квадратної сітки із однаковими вертикальними і горизонтальними відстанями, хоча можливі і інші конфігурації (наприклад Крос-КАМ). Оскільки в цифрових телекомунікаціях дані як правило двійкові, кількість точок в сітці як правило це ступінь числа 2 (2, 4, 8, …). Оскільки КАМ зазвичай квадратні, найпоширенішими загальноприйнятими формами її є 16-КАМ, 64-КАМ і 256-КАМ. Переходячи до сузір'їв більш високого порядку, стає можливим передавати більше біт на символ. Однак, якщо середня енергія сузір'я залишається незмінною, точки повинні знаходитися ближче одна до одної, і тому такий сигнал буде більш чутливим до шуму і іншого спотворення; це призведе до більшої частоти бітових помилок і тому КАМ вищого порядку може передавати більше даних з меншою надійністю доставки їх, ніж КАМ нижчого порядку при постійній середній енергії сузір'я. Для використання КАМ вищого порядку, без збільшення при тому частоти бітових помилок необхідно мати краще співвідношення сигнал/шум збільшуючи енергію сигналу, зменшуючи шум або і те і інше одночасно.

Коли частота передачі даних, яку треба забезпечити більше ніж така, яку може утворити 8-ФМн, зазвичай переходять до використання КАМ, оскільки вона дозволяє досягти більшої відстані між сусідніми точками в площині I-Q, більш рівномірно розподіляючи точки. Ускладненням є те, що точки більше не мають однакової амплітуди, і тому демодулятор тепер повинен правильно визначати як фазу так і амплітуду.

Див. також

• Модуляція (фізика)
• Квадратурно-фазова модуляція (КФМ)
• 16-позиційна КАМ
• Амплітудна модуляція
• Фазова модуляція
• Частотна модуляція