Малий зірчастий додекаедр

Малий зірчастий додекаедр Шаблон:Sfn Шаблон:RpШаблон:SfnШаблон:Rp — один з чотирьох правильних зірчастих багатогранників Кеплера — Пуансо.

Малий зірчастий додекаэдр вперше повністю описано в трактаті Йоганна Кеплера 1619 року «Harmonices Mundi»Шаблон:Rp, а назву йому дав Артур Кейлі в 1859 році. Шаблон:Sfn Шаблон:Rp

Позначення:

• W₂₀ (в нотації М. Веннінґера) Шаблон:Sfn
• U₃₄ (як однорідний багатогранник)
• C₄₃ (в нотації Г.Коксетера) Шаблон:Sfn ^{:стор.435}

Має 12 граней — правильних п'ятипроменевих зірок (пентаграм), які перетинаються між собою та 12 вершин. Шість пар граней лежать в паралельних площинах.

Його символ Шлефлі — $\{\frac{5}{2},5\}$. Це означає, що кожна вершина оточена 5-ма гранями (пентаграмами {5/2}). Шаблон:Sfn Шаблон:Rp

Має центральну опуклу ділянку кожної грані, «приховану» всередині, при цьому зовні видно тільки частину граней у вигляді рівнобедрених трикутніиків. Частина граней, що знаходиться всередині багатогранника відіграє роль плоскої мембрани та не розмежовує внутрішній простір багатогранника.

Шаблон:Не перекладено малого зірчастого додекаедра таке ж як і у правильного ікосаедра (тобто опукла оболонка малого зірчастого додекаедра є правильним ікосаедром). А розташування ребер малого зірчастого додекаедра таке ж як і у великого ікосаедра.

Малий зірчастий додекаедр має повну симетрію правильного ікосаедра, і отже, всі його елементи симетрії, а саме:

1) має 31 вісь обертової симетрії:

‒ 6 осей 5-го порядку — проходять через протилежні вершини;

‒ 10 осей 3-го порядку — проходять через протилежні точки, в яких перетинаються по три грані;

‒ 15 осей 2-го порядку — проходять через середини протилежних паралельних ребер.

2) має 15 площин дзеркальної симетрії, що проходять через кожні дві сусідні вершини та центр багатогранника (через кожну пару паралельних ребер).

3) має центр симетрії.

Як зірчаста форма додекаедра

Діаграма ззірчення правильного додекаедра та грань малого зірчастого додекаедра на ній	Жовтим кольором зображено грань малого зірчастого додекаедра	Утворення грані малого зірчастого додекаедра

Малий зірчастий додекаедр є першою зірчастою формою правильного додекаедра. Його грані складені з нульового та першого відсіків на діаграмі ззірчення правильного додекаедра. Шаблон:Sfn Шаблон:Rp

Малий зірчастий додекаедр утворюється з правильного додекаедра при продовженні його ребер до їх взаємного перетину, тобто кожна грань α правильного додекаедра замінюється зірчастим п'ятикутником з ядром α.Шаблон:Rp

Також малий зірчастий додекаедр є радіально-опуклим зірчастим багатогранником, тобто кожен промінь, що виходить з його центра, перетинає багатогранник лише в одній точці.

Як нарощення додекаедра

Часто малий зірчастий додекаедр визначається як багатогранник, утворений нарощенням на гранях додекаедра правильних п'ятикутних пірамід.

Сам Йоганн Кеплер називає цей багатогранник (малий зірчастий додекаедр) нарощеним додекаедром (а пізніше Echinus).

Це некоректне визначення іноді використовується й до цього часу. Наприклад, MathWorld стверджує, що малий зірчастий додекаедр може бути отриманий шляхом додавання правильних п'ятикутних пірамід до граней правильного додекаедра.

Однак це твердження придатне лише для полегшення візуалізації цього багатогранника, або для виготовлення його паперової моделі, або для обчислення його розмірів, але не для його визначення як тіла, так як при приєднанні (нарощенні) пірамід (з боковими гранями — золотими трикутниками) до граней додекаедра, в багатограннику присутні «хибні» вершини (ті, що знаходяться на перетині ребер), які насправді не є вершинами малого зірчастого додекаедра, а також додаткові ребра (два ребра п'ятикутних пірамід та одне ребро додекаедра лежать на одній прямій і візуально створюють враження одного ребра).

Багатогранник, утворений шляхом приєднання прямих п'ятикутних пірамід до граней додекаедра, є топологічно еквівалентним до Шаблон:Не перекладено (одного з тіл Каталана), та не є малим зірчастим додекаедром.

Ядро (Правильний додекаедр)	Зірчастий багатогранник	Багатогранник Каталана (Пентакісдодекаедр)

Топологія

Малий зірчастий додекаедр має 12 граней (пентаграм), при цьому ці пентаграми реретинаються по 30 ребрах в 12 вершинах. Отже, його характеристика Ейлера має значення $-6$, і ми можемо обчислити його рід за допомогою формули Ейлера:

$\mathrm{\Gamma }-P+B=2-2g$

Отже, $-6=2-2g$. Звідки випливає, що малий зірчастий додекаедр має рід $g=4$ . Це спостереження, зроблене Луї Пуансо, спочатку викликало плутанину, але Фелікс Кляйн показав у 1877 році, що малий зірчастий додекаедр можна розглядати як розгалуджене покриття сфери Рімана рімановою поверхнею роду 4, з точками розгалуження в центрі кожної пентаграми. Насправді ця ріманова поверхня, яка називається Шаблон:Не перекладено, має найбільшу кількість симетрій серед будь-яких ріманових поверхонь роду 4: група симетрії $S_5$ виступає як автоморфізм.

Формули

У всіх формулах нижче: $\phi =\frac{1+\sqrt{5}}{2}\approx 1.6180339887$ — відношення пропорції «золотого перетину». (Шаблон:OEIS). Шаблон:Clear

Для малого зірчастого додекаедра з довжиною ребра $a$:
Довжина основи рівнобедреного трикутника грані (довжина сторони базового додекаедра)	$b=(\sqrt{5}-2)\cdot a=\frac{1}{{\phi }^3}\cdot a$	≈ 0.236067977$\cdot a$
Довжина бічної сторони рівнобедреного трикутника грані	$s=\frac{3-\sqrt{5}}{2}\cdot a=(2-\phi )\cdot a=\frac{1}{{\phi }^2}\cdot a$	≈ 0.381966011$\cdot a$
Висота «нарощеної піраміди»	$H=R-r=\sqrt{\frac{5-2\sqrt{5}}{5}}\cdot a=\frac{1}{\phi \cdot \sqrt{\phi +2}}\cdot a$	≈ 0.324919696$\cdot a$
Радіус описаної сфери (проходить через всі вершини)	$R=\frac{1}{2}\cdot \sqrt{\frac{5-\sqrt{5}}{2}}\cdot a=\frac{\sqrt{3-\phi }}{2}\cdot a$	≈ 0.587785252$\cdot a$
Радіус напіввписаної сфери (дотикається до всіх ребер)	$\rho =\frac{\sqrt{5}-1}{4}\cdot a=\frac{\phi -1}{2}\cdot a$	≈ 0.309016994$\cdot a$
Радіус вписаної сфери (дотикається до всіх граней)	$r=\frac{1}{2}\cdot \sqrt{\frac{5-\sqrt{5}}{10}}\cdot a=\frac{1}{2}\sqrt{\frac{3-\phi }{5}}\cdot a$	≈ 0.262865556$\cdot a$
Площа поверхні	$S=15\cdot \sqrt{85-38\sqrt{5}}\cdot a^2=15\cdot (5-3\phi )\sqrt{3-\phi }\cdot a^2$	≈ 2.572701377$\cdot a^2$
Об'єм	$V=V_{\text{додек}}+12\cdot V_{\text{пірам}}=\frac{5}{4}\cdot (5\sqrt{5}-11)\cdot a^3$	≈ 0.225424859$\cdot a^3$
Двогранний кут між гранями	$\alpha =\arccos (-\frac{\sqrt{5}}{5})=2\cdot \arctan (\phi )$	≈ 2.034443935рад ≈ 116°33′ 54.1842′′

Центр мас малого зірчастого додекаедра знаходиться в його геометричному центрі.

Момент інерції суцільного малого зірчастого додекаедра з масою Шаблон:Mvar та довжиною ребра Шаблон:Mvar (вісь обертання проходить через протилежні вершини):

$I=\frac{35-9\cdot \sqrt{5}}{300}\cdot m\cdot a^2\approx 0.049584627341\cdot m\cdot a^2$

Описана сфера малого зірчастого додекаедра

Напіввписана сфера малого зірчастого додекаедра

Вписана сфера малого зірчастого додекаедра

Вписана та напіввписана сфери повністю лежать всередині багатогранника та не виходять за його межі.

Координати вершин

Вершини малого зірчастого додекаедра в декартовій системі координат

Малий зірчастий додекаедр з довжиною ребра $a=1$ в декартовій системі координат має вершини з наступними координатами:

• $(-\sqrt{\frac{3-\sqrt{5}}{6}},0,\frac{1}{2}\cdot \sqrt{\frac{3+\sqrt{5}}{6}}),$ $(\frac{1}{2}\cdot \sqrt{\frac{3-\sqrt{5}}{6}},\pm \frac{\sqrt{5}-1}{4},\frac{1}{2}\cdot \sqrt{\frac{3+\sqrt{5}}{6}});$
• $(\sqrt{\frac{3-\sqrt{5}}{6}},0,-\frac{1}{2}\cdot \sqrt{\frac{3+\sqrt{5}}{6}}),$ $(-\frac{1}{2}\cdot \sqrt{\frac{3-\sqrt{5}}{6}},\pm \frac{\sqrt{5}-1}{4},-\frac{1}{2}\cdot \sqrt{\frac{3+\sqrt{5}}{6}});$
• $(\frac{\sqrt{3}}{3},0,\frac{1}{2}\cdot \sqrt{\frac{7-3\sqrt{5}}{6}}),$ $(-\frac{\sqrt{3}}{6},\pm \frac{1}{2},\frac{1}{2}\cdot \sqrt{\frac{7-3\sqrt{5}}{6}});$
• $(-\frac{\sqrt{3}}{3},0,-\frac{1}{2}\cdot \sqrt{\frac{7-3\sqrt{5}}{6}}),$ $(\frac{\sqrt{3}}{6},\pm \frac{1}{2},-\frac{1}{2}\cdot \sqrt{\frac{7-3\sqrt{5}}{6}}).$

При цьому вершини лежать в чотирьох паралельних площинах (паралельних до площини Oxy), в кожній з яких розташовані як вершини правильного трикутника.

Початок координат збігається з центром багатогранника, що є його центром симетрії та центром вписаної, напіввписаної та описаної сфер.

Вісь Oz збігається з однією з осей симетрії 3-го порядку, а вісь Oy — з однією з осей симетрії 2-го порядку.

Площина Oxz збігається з однією з площин симетрії багатогранника.

Пов'язані та споріднені багатогранники

Опукла оболонка малого зірчастого додекаедра є правильним ікосаедром.

Ребра малого зірчастого додекаедра збігаються з ребрами великого ікосаедра; поєднання цих двох багатогранників утворює вироджений багатогранник, що має назву Шаблон:Не перекладено.

Анімація послідовності зрізання малого зірчастого додекаедра від { Шаблон:Frac, 5} до {5, Шаблон:Frac}

Існує чотири неопуклих однорідних багатогранників, що утворені певними ступенями операції зрізання малого зірчастого додекаедра.

Зрізаний малий зірчастий додекаедр можна вважати виродженим однорідним багатогранником. Вершини малого зірчастого додекаедра зрізаються, поки процес не досягає площин пентаграм під ними.

Візуально він виглядає як правильний додекаедр, але має 24 подвійно-накриті грані — 12 п'ятикутників, утворених від зрізання вершин і 12 п'ятикутників, утворених від зрізання пентаграм, які перекривають перші 12 п'ятикутників. П'ятикутники із зрізаних пентаграм насправді є виродженими десятикутниками {10/2}, що приймають форму подвійно-накритих п'ятикутників із двома множинами вершин і ребер, накладених одне на одне.

Коли Шаблон:Frac -кутник скорочується в процесі зрізання, він стає Шаблон:Frac -кутником.

Наприклад, зрізаний п'ятикутник { Шаблон:Frac} стає десятикутником { Шаблон:Frac}, а зрізана пентаграма { Шаблон:Frac} стає подвійно-накритим п'ятикутником (тобто десятикутником, що має форму п'ятикутника) { Шаблон:Frac} (це означає, що ми відвідаємо кожну вершину двічі, щоб завершити багатокутник).

Багатогранник має 60 вершин (в кожній вершині «додекаедра» містяться три вершини багатогранника) та 90 ребер (кожне ребро «додекаедра» є потрійним — одне ребро від зрізання вершини (вершинна фігура — опуклий правильний п'ятикутник) та два ребра від зрізання пентаграми).

Шаблон:Не перекладено утворюється при Шаблон:Не перекладено (ректифікації) малого зірчастого додекаедра, коли зрізання вершин проводиться до точок, що лежать на серединах ребер багатогранника, тобто ребра початкового багатогранника фактично зникають.

Шаблон:Не перекладено є однорідним неопуклим багатогранником U₃₇, що має діаграму Коксетера — Динкіна Шаблон:CDD та символ Шлефлі t{5,5/2}. Має 24 граней (12 правильних п'ятипроменевих зірок (пентаграм) та 12 правильних десятикутників), 90 ребер та 60 вершин.

Процес зрізання малого зірчастого додекаедра завершується (при повному глибокому зрізанні або біректифікації) утворенням двоїстого до нього багатогранника — великого додекаедра, коли грані початкового багатогранника зменшуються до точок, тобто фактично зникають.

Назва	Малий зірчастий додекаедр	Зрізаний малий зірчастий додекаедр	Шаблон:Не перекладено	Шаблон:Не перекладено	Великий додекаедр
Діаграма Коксетера — Динкіна	Шаблон:CDD o5o5/2x	Шаблон:CDD o5x5/2x	Шаблон:CDD o5x5/2o	Шаблон:CDD x5x5/2o	Шаблон:CDD x5o5/2o
Символ Шлефлі	{5/2,5}	t{5/2,5}	r{5,5/2}	t{5,5/2}	{5,5/2}
Зображення

Родина зірчастих форм правильного додекаедра.

Зірчасті форми правильного додекаедра
	Тіло Платона	Тіла Кеплера — Пуансо
	Додекаедр	Малий зірчастий додекаедр	Великий додекаедр	Великий зірчастий додекаедр
Символ Шлефлі {p, q}	{5,3}	{5/2,5}	{5,5/2}	{5/2,3}
Зображення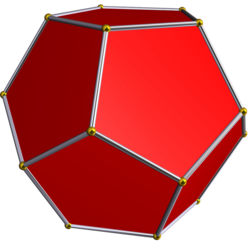
Діаграма зірчастого многогранника
Обертання

Топологічно еквівалентний багатогранник до малого зірчастого додекаедра

Малий зірчастий додекаедр з піритоедричною симетрією

Два однорідних з'єднання багатогранників складаються з малих зірчастих додекаедрів:

З'єднання двох малих зірчастих додекаедрів	З'єднання п'яти малих зірчастих додекаедрів

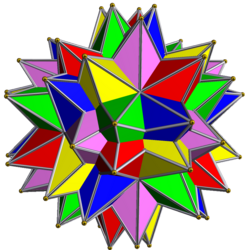
Додатково

Обертання багатогранника	Сферична проєкція	Розгортка	Паперова модель багатогранника
	Цей багатогранник також можна подати у вигляді сферичної плитки зі щільністю 3. (Одна сферична грань пентаграми, обведена синім і заповнена жовтим кольорами)	Шаблон:Nowrap Малий зірчастий додекаедр можна скласти з паперу, з'єднавши разом 12 правильних п'ятикутних пірамід. Кожен рівнобедрений трикутник (золотий трикутник) в цій розгортці візуально представляє частину пентаграми — грані малого зірчастого додекаедра.

Шаблон:Не перекладено малого зірчастого додекаедра
Просторовими Шаблон:Не перекладено малого зірчастого додекаедра є 10 просторових шестикутників.

В мистецтві та архітектурі

Мозаїка Паоло Учелло, 1430

• Малий зірчастий додекаедр можна побачити в мозаїці полу в соборі Святого Марка в Венеції, автор Паоло Учелло, біля 1430 року.
• Багатогранник є центральною фігурою в двох літографіях Ешера — Контраст (Порядок і хаос) (1950) та Гравітація^[en] (1952).

Скульптура в Шаблон:Не перекладено

Скульптура за мотивами «Гравітації» Моріца Корнеліса Ешера, представлена ​​в Університеті Твенте

Див. також

• Однорідний зірчастий многогранник
• Шаблон:Не перекладено

Література

• Шаблон:Cite book
• Шаблон:Cite book
• Шаблон:Стаття
• Шаблон:Книга
• Шаблон:Cite journal
• Шаблон:Cite journal

• Шаблон:Стаття

• Шаблон:Cite journal

Посилання

• Шаблон:MathWorld
  • Шаблон:MathWorld
• Шаблон:Polytope Wiki
• Шаблон:Dmccooey
• Nan Ma. «Small stellated dodecahedron {5/2, 5}»
• Klitzing, Richard. «sissid»
• Однорідні багатогранники та двоїсті до них
• Stellation and facetting — a Brief History
• Paper Small Stellated Dodecahedron

Шаблон:Нк Шаблон:Багатогранники