Трисхилий купол

У геометрії трисхилий купол — призматоїд, що складається з правильного шестикутника (нижня основа купола), правильного трикутника (верхня грань, що паралельна основі), та бічних граней: 3 прямокутників та 3 рівнобедрених трикутників.

Належить до родини куполів і є підкласом призматоїдів.

Два куполи можуть бути з'єднані по їх нижній основі, утворюючи багатогранник Шаблон:Не перекладено, в прямій (якщо з'єднані однойменні грані) або повернутій (якщо з'єднані різнойменні грані) орієнтації.

Багатогранник Джонсона Шаблон:Math

Трисхилий купол
Тип	Багатогранник Джонсона J3 Призматоїд, множина куполів.
Властивості	Опуклий, рівносторонній, правильногранний
Комбінаторика
Елементи	8 граней ((3+1){3} + 3{4} + 1{6}) 15 ребер 9 вершин: 6 вершин (3-го степеня) + 3(4-го)
Грані	3+1 Правильних трикутників, 3 Квадрата, 1 Правильний шестикутник.
Характеристика Ейлера	$\chi =\mathrm{\Gamma }-\text{P}+\text{B}=2$
Конфігурація вершини	6(3.4.6) 3(3.4.3.4)
Вершинна фігура	3 прямокутника з довжинами сторін 1 та $\sqrt{2}$ 6 трикутників з довжинами сторін 1, $\sqrt{2}$, $\sqrt{3}$
Класифікація
Позначення	• J3 (в нотації Шаблон:Не перекладено) • M4 (в нотації ЗалгаллераШаблон:Sfn) • U3 = Q3 Шаблон:Sfn (в Шаблон:Не перекладено) • Q3 (в нотації Стюарта)
Символ Шлефлі	{3} || t{3}
Група симетрії	Шаблон:Не перекладено, [3], (*33), порядок 6 (Циклічна симетрія 3-Піраміди)
Група поворотів	C3, [3]+, (33), порядок 3
Двоїстий багатогранник	Напіврозсічений трикутний трапецоедр
Розгортка

Рівносторонній трисхилий купол є одним із багатогранників Джонсона (Шаблон:Math або Шаблон:Math (за ЗалгаллеромШаблон:Sfn).

Трисхилий купол можна розглядати як половину кубооктаедра.

Багатогранник Джонсона — один із 92 строго опуклих багатогранників, що мають правильні грані, але не є однорідним (тобто він не є правильним багатогранником, архімедовим тілом, призмою або антипризмою). Правильногранні багатогранники названі ім'ям Шаблон:Не перекладено, який першим перелічив їх в 1966 р. Шаблон:Sfn

Трисхилий купол складено з 8 граней: 3+1 = 4 правильних трикутників, 3 квадратів та 1 правильного шестикутника.

Одна трикутна грань оточена трьома квадратами; три трикутних граней оточені двома квадратними та однією шестикутною гранню; квадратні грані оточені трьома трикутними та однією шестикутною гранями; шестикутна грань оточена трьома трикутними та трьома квадратними гранямиШаблон:Джерело.

Має 15 ребер однакової довжини: 3+6 = 9 ребер розташовані між квадратною та трикутною гранями, 3 ребра — між трикутною та шестикутною гранями, решта 3 — між квадратною та шестикутною гранями.

У трисхилого купола 9 вершин: 3 вершини оточені двома трикутними та двома квадратними гранями (почергово); 6 вершин оточені трикутною, квадратною та шестикутною гранями.

Трисхилий купол може бути отриманий шляхом поділу навпіл кубооктаедра по шестикутному перерізу між двома протилежними трикутними гранями.

Навпаки, два трисхилих куполи можна поєднати у поверненій орієнтації по шестикутній грані, і отримати кубооктаедр.

Трисхилий купол має вісь поворотної симертії 3-го порядку, що проходить через центри основ; а також три площини дзеркальної симетрії, що проходять через вісь купола та середини сторін нижньої основиШаблон:Джерело.

Формули

Діагоналі

Кількість діагоналей опуклого багатогранника: $(\genfrac{}{}{0ex}{}{B}{2})-P$ , де В — кількість вершин, Р — кількість ребер багатогранника. Для трисхилого купола:

$(\genfrac{}{}{0ex}{}{9}{2})-15=\frac{9}{2}\cdot \frac{8}{1}-15=21$ діагоналі (15 граневих та 6 просторових).

Діагоналі трисхилого купола з довжиною ребра $a$
	Граневі діагоналі	$AB=\sqrt{2}\cdot a\approx 1.41421356237\cdot a$ $AC=\sqrt{3}\cdot a\approx 1.73205080756\cdot a$ $AD=2\cdot a$
	Просторові діагоналі	$FC=\sqrt{3}\cdot a\approx 1.73205080756\cdot a$

Метричні характеристики

Описана сфера трисхилого купола

Середньовписана сфера трисхилого купола

Для трисхилого купола з довжиною ребра $a$:
Радіус описаної сфери (проходить через всі вершини)		$R=a$
Радіус напіввписаної сфери (дотикається до всіх ребер)		$\rho =\frac{\sqrt{3}}{2}\cdot a$	$\approx 0.8660254\cdot a$
Вписаної сфери трисхилий купол не має
Висота H (Відстань між паралельними трикутною та шестикутною гранями)		$H=\frac{\sqrt{6}}{3}\cdot a$	$\approx 0.81649658\cdot a$
Площа поверхні		$S=(3+\frac{5\sqrt{3}}{2})\cdot a^2$	$\approx 7.33012701\cdot a^2$
Об'єм		$V=\frac{5}{6}\sqrt{2}\cdot a^3$	$\approx 1.1785113\cdot a^3$

Кути

Плоскі кути граней при вершині: 60°, 90°, 120°.

Кути багатогранника
Кут між несусідніми ребрами при вершині верхньої основи	$\phi =\arccos (-\frac{1}{2})$	$=\frac{2\pi }{3}$ rad = 120°
Двогранний кут між гранями {3} та {4}	$\alpha =\arccos (-\frac{\sqrt{3}}{3})=\mathrm{arcsec}(-\sqrt{3})$	≈ 2.1862760354 rad ≈ 125°15′ 51.8028′′
Двогранний кут між гранями {3} та {6}	$\beta =\arccos \left(\frac{1}{3}\right)=\mathrm{arcsec}\left(3\right)$	≈ 1.2309594173 rad ≈ 70° 31′ 43.60571′′
Двогранний кут між гранями {4} та {6}	$\gamma =\arccos \left(\frac{\sqrt{3}}{3}\right)=\mathrm{arcsec}\left(\sqrt{3}\right)$	≈ 0.9553166181 rad ≈ 54°44′ 8.197142′′
Тілесний кут при вершині нижньої основи (шестикутної)	${\mathrm{\Omega }}_1=\frac{1}{2}\arccos (-\frac{7}{9})=2\arcsin \left(\frac{\sqrt{3}}{3}\right)=$ $=4\arctan (\sqrt{3}-\sqrt{2})$	$\mathrm{\Omega }\approx 1.2309594$ ср
Тілесний кут при вершині верхньої основи (трикутної)	${\mathrm{\Omega }}_2=\arccos (-\frac{7}{9})=4\arcsin \left(\frac{\sqrt{3}}{3}\right)=$ $=8\arctan (\sqrt{3}-\sqrt{2})$	${\mathrm{\Omega }}_2\approx 2.4619188$ ср
Сферичність	$\mathrm{\Psi }=\frac{2\sqrt[3]{50\pi }}{6+5\sqrt{3}}$	$\mathrm{\Psi }\approx 0.7360858$

Центр тяжіння трисхилого купола лежить на його осі симетрії на відстані $\frac{\sqrt{6}}{8}\cdot a$ від нижньої основи.

Двоїстий багатогранник

Трисхилий купол не має ні топологічно-двоїстого багатогранника (вершини двоїстого знаходяться в центрах граней вихідного багатогранника), ні канонічно-двоїстого багатогранника (середньовписані сфери обох багатогранників збігаються).

Його двоїстий може бути побудований лише загальним чином (кожній грані вихідного багатогранника відповідає вершина двоїстого, кожній вершині вихідного — грань дуального, з дотриманням симетрії вихідного багатогранника), а тому форми та розміри двоїстого багатогранника до вихідного трисхилого купола можуть різнитися.

Двоїстий до трисхилого купола має 9 граней: 6 трикутників + 3 дельтоїда; 15 ребер, 8 вершин.

Обертання двоїстого до трисхилого купола багатогранника

Двоїстий багатогранник	Розгортка двоїстого

Споріднені багатогранники

Трисхилий купол належить до родини куполів. Сімейство n-куполів з правильними гранями існує до n = 5 включно.Шаблон:Куполи Два трисхилих куполи можуть бути з'єднані своїми шестикутними основами в прямій орієнтації (поєднуються однойменні бокові грані); отриманий багатогранник — Шаблон:Не перекладено (J₂₇). Якщо один з куполів повернути на 60º, то отримаємо триcхилий повернутий бікупол, більш відомий як [[Кубооктаедр|кубоктаедрШаблон:Джерело]].

Трисхилий прямий бікупол	Трисхилий повернутий бікупол (кубооктаедр)

Нарощений трисхилий купол, майже-багатогранник Джонсона з компланарними гранями

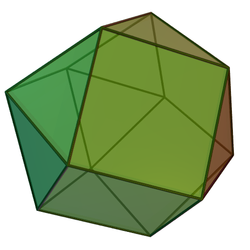
Трисхилий купол можна наростити трьома квадратними пірамідами, залишаючи суміжні копланарні грані без змін. Отриманий багатогранник, нарощений трисхилий купол, належить до родини Шаблон:Не перекладено з компланарними гранями.

Якщо об'єднати ці копланарні трикутники в єдині грані, отримаємо топологічно ще один трисхилий купол, бічні грані якого є рівнобедреними трапеціями. Якщо всі трикутні грані зберегти без змін, а шестикутник в основі розбити на 6 трикутників, вийде копланарний дельтаедр з 22 гранямиШаблон:Джерело.

Література

• Шаблон:Стаття (Містить оригінальне перерахування 92 тіл і гіпотезу, що інших немає.)
• Шаблон:Книга (Перший доказ, що існує тільки 92 тіл Джонсона.)

Посилання

• Шаблон:MathWorld
• Polytope Wiki.Triangular_cupola
• McCooey, David.TriangularCupola.
• Klitzing, Richard. «tricu»
• Quickfur. «The Triangular Cupola»