Центральна гранична теорема
Центральна гранична теорема — теорема теорії ймовірностей про збіжність розподілу суми незалежних однаково розподілених випадкових величин до нормального розподілу. Ця теорема підкреслює особливість нормального розподілу в теорії ймовірностей.
Наприклад, отримано вибірку, яка містить велику кількість спостережень, кожне з яких було отримано випадковим чином і вони не залежать від інших спостережень, і на основі значень цих спостережень розраховують арифметичне середнє. Якщо цю процедуру повторити багато разів, центральна гранична теорема стверджує, що розраховані середні значення будуть мати нормальний розподіл. Простим прикладом цього є багаторазове підкидання монети при яких імовірність випадіння заданої кількості гербів у всій послідовності подій буде наближатися до нормальної кривої, із середнім, що знаходитиметься по середині від загальної кількості випадань монети на кожну сторону. (Граничне значення для нескінченної кількості підкидань буде дорівнювати нормальному розподілу.)
Центральна гранична теорема має декілька варіантів. У своїй загальній формі, випадкові величини повинні бути однаково розподілені. У деяких варіантах, збіжність середнього значення прямує до нормального розподілу також і у випадку не однаково розподілених величин, або не лише при незалежних спостереженнях, що буде здійснюватися за умови виконання певних умов.
У перших версіях цієї теореми, нормальний розподіл може використовуватися як апроксимація біноміального розподілу, що відомо як локальна теорема Муавра — Лапласа.
Центральна гранична теорема для незалежних послідовностей

Класичне формулювання
Нехай — послідовність взаємно незалежних випадкових величин з однаковими розподілами, які мають скінченне математичне сподівання та скінченну дисперсію .
Нехай . Тоді
А для довільних фіксованих справедливо:
Де — нормальна функція розподілу[2][3].
Формулювання Ляпунова
Теорема названа на честь російського математика Олександра Ляпунова. У цьому варіанті центральної граничної теореми випадкові величини мають бути незалежними, але не обов'язково однаково розподіленими. Теорема також вимагає щоб випадкові величини мали скінченні моменти деякого порядку Шаблон:Nowrap і швидкість зростання цих моментів має бути обмежена умовою Ляпунова.
ЦГТ Ляпунова[4]: Нехай {Xi} — послідовність незалежних випадкових величин, таких, що кожна з них має скінченне математичне сподівання і дисперсію . Позначимо . Якщо для деякого виконується умова Ляпунова
Тоді сума прямує за розподілом до стандартного нормального розподілу, при
На практиці зазвичай найлегше перевірити умову Ляпунова для . Якщо послідовність випадкових величин задовольняє умову Ляпунова, то вона задовольняє також умову Лінденберга. Зворотне твердження не правильне.
Формулювання Ліндеберга
Шаблон:Main Використовуючи ті позначення що й у попередньому параграфі, замінюючи умову Ляпунова на слабшу (запропоновану фінським математиком Ліндебергом у 1920 році) можна отримати нове формулювання центральної граничної теореми.
- Якщо для кожного виконується
- де — характеристична функція. Тоді розподіл стандартизованої суми Zn прямує до стандартного нормального розподілу N(0,1).
Багатовимірна ЦГТ
Доведемо, що характеристичні функції можна розширити до випадку, коли кожна окрема величина Шаблон:Math є випадковим вектором у Шаблон:Math, із вектором середніх значень Шаблон:Math і матрицею коваріацій Шаблон:Math (між компонентами вектора), і ці випадкові вектори є незалежними і однаково розподіленими. Сумування цих векторів виконується поелементно. Багатовимірна центральна гранична теорема стверджує, що при масштабуванні, суми збігаються до багатовимірного нормального розподілу.[5]
Припустимо, що
це Шаблон:Mvar-вимірний вектор. Виділення жирним шрифтом для Шаблон:Math означає, що це випадковий вектор, а не випадкова (одновимірна) величина. Тоді сума випадкових векторів дорівнюватиме
а середнє дорівнюватиме
і таким чином
Багатовимірна центральна гранична теорема стверджує, що
де коваріаційна матриця Шаблон:Math дорівнює
А швидкість збіжності задається наступним результатом Шаблон:Нп:
Теорема.[6] Нехай
незалежні випадкові вектори із області значень
, кожний з яких має нульове середнє. Запишемо
і припустимо
є зворотньою. Нехай
буде
-вимірним Гаусовим розподілом із тим самим середнім і коваріаційною матрицею як у
. Тоді для всіх опуклих множин
,
де це універсальна стала, , і позначає Евклідову норму для .
Не відомо чи множник є необхідним.[7]
Узагальнена теорема
Центральна гранична теорема стверджує, що сума деякої кількості незалежних і однаково розподілених випадкових величин із скінченною дисперсією буде прямувати до нормального розподілу із збільшенням кількості цих величин. Узагальнена її версія, яку запропонували Гнєденко і Колмогоров стверджує, що сума деякої кількості випадкових величин із розподілами, що мають хвіст, який відповідає степеневому закону (Хвіст розподілу Парето), зменшується як |x|Шаблон:Math де Шаблон:Math (і таким чином має нескінченну дисперсію) буде прямувати до стійкого розподілу Шаблон:Math із тим як кількість елементів суми збільшується.[8][9] Якщо Шаблон:Math, тоді сума збігається до стійкого розподілу із параметром стабільності який дорівнює 2, тобто Гауссового розподілу.[10]
Доведення класичної ЦГТ
Центральна гранична теорема має просте доведення за допомогою характеристичних функцій.[11] Воно подібне до доведення (слабкого) закону великих чисел.
Припустимо Шаблон:Math} є незалежними і однаково розподіленими випадковими величинами, кожна з яких має середнє Шаблон:Mvar і скінченну дисперсію Шаблон:Math. Сума Шаблон:Math має середнє Шаблон:Mvar і дисперсію Шаблон:Math. Розглянемо випадкову величину
де в останньому кроці ми визначили нові випадкові величини Шаблон:Math, кожна з яких має нульове середнє і одиничну дисперсію (Шаблон:Math). Характеристична функція для Шаблон:Mvar має вигляд
Де в останньому кроці ми застосували факт, що всі Шаблон:Mvar однаково розподілені. Відповідно до теореми Тейлора характеристична функція для Шаблон:Math матиме вигляд,
де Шаблон:Math є "[[Нотація_Ландау|нотацією маленького Шаблон:Mvar]]" для деякої функції від Шаблон:Mvar, яка прямує до нуля набагато швидше ніж Шаблон:Math. Відповідно до границі показникової функції (Шаблон:Math), характеристична функція для Шаблон:Mvar дорівнює
Зауважимо, що всі терми старшого порядку в даному виразі зникають при границі де Шаблон:Math. Права сторона виразу дорівнює характеристичній функції стандартного нормального розподілу Шаблон:Math, із чого разом із Шаблон:Нп випливає, що розподіл Шаблон:Mvar буде наближатися до Шаблон:Math з тим як Шаблон:Math. Таким чином, сума Шаблон:Math буде наближатися до нормального розподілу Шаблон:Math, і значення вибіркового середнього
збігається до нормального розподілу Шаблон:Math, з чого випливає центральна гранична теорема.
Застосування і приклади
Простий приклад
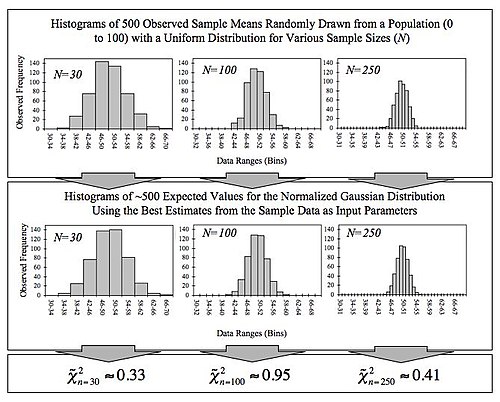
Простим прикладом центральної граничною теореми є підкидання великої кількості ідентичних гральних кісток. Розподіл суми (або середнього) від тих чисел що випадуть буде добре апроксимуватися за допомогою нормального розподілу. Оскільки величини реального світу часто є збалансованою сумою багатьох неспостережувальних випадкових подій, центральна гранична теорема також частково пояснює те, що нормальний розподіл зустрічається досить часто. Вона також виправдовує застосування апроксимації для великих статистичних вибірок до нормального розподілу у контрольованих експериментах.

Типові застосування з реального життя
У літературі можна знайти велику кількість корисних і цікавих прикладів застосувань, пов'язаних із центральною граничною теоремою.[12] Одним із таких прикладів[13] є наступні ситуації:
- Розподіл імовірності загальної пройденої відстані у випадковому блуканні (зміщеної або незміщеної) буде прямувати до нормального розподілу.
- Підкидання великої кількості монет буде мати нормальний розподіл для загальної кількості випадання аверсів (або реверсів).
З іншої точки зору, центральна гранична теорема пояснює common appearance "дзвоноподібної кривої" при оцінках функції густини застосованих до даних реального світу. В таких випадках як електричний шум, екзаменаційні оцінки, і так далі, ми часто можемо розглядати одне конкретне вимірюване значення як зважене середнє великої кількості малих випадкових впливів. Використавши узагальнення центральної граничної теореми, ми можемо побачити, що дуже часто (хоча не завжди) це утворюватиме в результаті розподіл, що наближений до нормального.
В загальному розумінні, чим більше вимірювання є подібним до суми випадкових величин із однаковим впливом на результат, тим ближче воно буде до нормального розподілу. Це обґрунтовує поширене використання цього розподілу як такого, що відповідає впливам неспостережувальних змінних у моделях, таких як лінійні моделі.
Див. також
Джерела
- Шаблон:Карташов.Імовірність процеси статистика
- Шаблон:Гнеденко.Курс теории вероятностей
- Шаблон:Гіхман.Скороход.Ядренко
- Шаблон:CitationШаблон:Ref-en
Примітки
- ↑ Шаблон:Cite book
- ↑ Шаблон:Cite book
- ↑ Шаблон:Cite paper
- ↑ Шаблон:Harvtxt
- ↑ Шаблон:Cite book
- ↑ Ryan O’Donnell (2014, Theorem 5.38) http://www.contrib.andrew.cmu.edu/~ryanod/?p=866 Шаблон:Webarchive
- ↑ Шаблон:Cite journal
- ↑ Шаблон:Cite book
- ↑ Шаблон:Cite book
- ↑ Шаблон:Cite book
- ↑ Шаблон:Cite web
- ↑ Dinov, Christou & Sánchez (2008)
- ↑ Шаблон:Cite web