Формула тангенса половинного кута

Геометричне доведення формули тангенса половинного кута

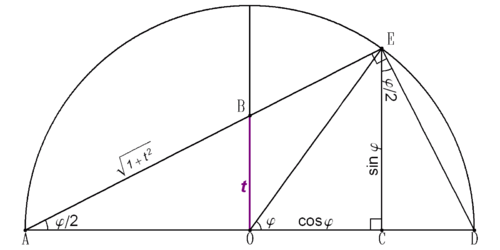
Формула тангенса половинного кута — формула, що пов'язує тангенс половинного кута с тригонометричними функціями повного кута:

$\mathrm{tg}\frac{\theta }{2}=\frac{\sin \theta }{1+\cos \theta }=\frac{1-\cos \theta }{\sin \theta }=(-1{)}^k\sqrt{\frac{1-\cos \theta }{1+\cos \theta }},$

де $k\in \mathbb{Z}$ і визначається умовою $k\pi \le \theta \le (k+1)\pi$.

З цією формулою пов'язані наступні формули:

$\begin{array}{cc}\mathrm{tg}\frac{\alpha +\beta }{2}& =\frac{\sin \alpha +\sin \beta }{\cos \alpha +\cos \beta },\\ \mathrm{tg}(\frac{\theta }{2}+\frac{\pi }{4})& =\sec \theta +\mathrm{tg}\theta =\frac{1+\mathrm{tg}(\theta /2)}{1-\mathrm{tg}(\theta /2)}=(-1{)}^k\sqrt{\frac{1+\sin \theta }{1-\sin \theta }},\\ \mathrm{c}\mathrm{t}\mathrm{g}(\frac{\theta }{2}+\frac{\pi }{4})& =\sec \theta -\mathrm{tg}\theta =\frac{1-\mathrm{tg}(\theta /2)}{1+\mathrm{tg}(\theta /2)}=(-1{)}^k\sqrt{\frac{1-\sin \theta }{1+\sin \theta }}.\end{array}$

де $k\in \mathbb{Z}$ і визначається умовою $(k-\frac{1}{2})\pi \le \theta \le (k+\frac{1}{2})\pi$.

При $\theta \in (-\frac{\pi }{2},\frac{\pi }{2})$ отримуємо: $\mathrm{tg}\frac{\theta }{2}=\frac{\mathrm{tg}\theta }{1+\sqrt{1+{\mathrm{tg}}^2\theta }}.$

Універсальна тригонометрична підстановка в інтегральному численні

Буває корисно записувати тригонометричні функції через раціональні функції нової змінної $t$, що дорівнює тангенсу половинного кута.

$\cos \phi =\frac{1-t^2}{1+t^2},$	$\sin \phi =\frac{2t}{1+t^2},$
$\mathrm{tg}\phi =\frac{2t}{1-t^2},$	$\mathrm{ctg}\phi =\frac{1-t^2}{2t},$
$\sec \phi =\frac{1+t^2}{1-t^2},$	$\csc \phi =\frac{1+t^2}{2t},$
$e^{i\phi }=\frac{1+it}{1-it},$	$e^{-i\phi }=\frac{1-it}{1+it}.$

В цих формул можна виразити арктангенс через натуральний логарифм

$\mathrm{arctg}(t)=\frac{1}{2i}\ln \frac{1+it}{1-it}.$

При знаходженні превісних, що містять sin(φ) та cos(φ), підстановка після заміни:

$t=\mathrm{tg}\frac{1}{2}\phi .$

та

$\phi =2\mathrm{arctg}(t),$

виглядає

$d\phi =\frac{2dt}{1+t^2}.$

Гіперболічні тотожності

Можна отримати аналогічні формули для гіперболічних функцій.

$t=\mathrm{th}\frac{1}{2}\theta =\frac{\mathrm{sh}\theta }{\mathrm{ch}\theta +1}=\frac{\mathrm{ch}\theta -1}{\mathrm{sh}\theta }$

Отимуємо

$\mathrm{ch}\theta =\frac{1+t^2}{1-t^2},$	$\mathrm{sh}\theta =\frac{2t}{1-t^2},$
$\mathrm{th}\theta =\frac{2t}{1+t^2},$	$\mathrm{cth}\theta =\frac{1+t^2}{2t},$
$\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}\theta =\frac{1-t^2}{1+t^2},$	$\mathrm{c}\mathrm{s}\mathrm{c}\mathrm{h}\theta =\frac{1-t^2}{2t},$
$e^{\theta }=\frac{1+t}{1-t},$	$e^{-\theta }=\frac{1-t}{1+t}.$

Відповідно, для арктангенса та натурального логарифма отримуємо:

$\mathrm{arth}(t)=\frac{1}{2}\ln \frac{1+t}{1-t}.$

Див. також

• Список тригонометричних тотожностей
• Функція Гудермана

Джерела

• Тангенс половинного кута Шаблон:Webarchive на Planetmath