Кардіоїда
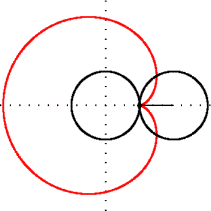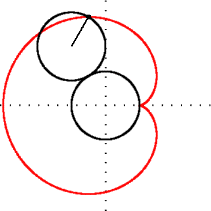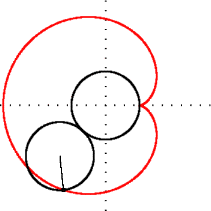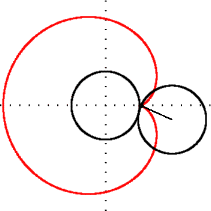
Шаблон:UniboxКардіоїда (Шаблон:Lang-el — серце, Шаблон:Lang-el — вид) — пласка лінія, яка описується фіксованою точкою кола, що котиться без ковзання по нерухомому колу такого ж радіуса.
Отримала свою назву за схожість своїх обрисів зі стилізованим зображенням серця.
Рухоме коло називається твірним, нерухоме коло — напрямним.Шаблон:Sfn Шаблон:Rp
Кардіоїда є окремим випадком равлика Паскаля, епіциклоїди і синусоїдальної спіралі.
Кардіоїда є інверсією (оберненою кривою) параболи з центром інверсії в її фокусі, відносно кола з цим же центром.[1]
Кардіоїду можна окреслити як множину точок відбиття фіксованої точки деякого фіксованого кола відносно всіх дотичних до цього кола.[2] Шаблон:Sfn Шаблон:Rp
Рівняння
Нехай — радіус двох твірних кіл з центрами в точках , — кут повороту рухомого кола, а початок координат — початкова точка (також вона є точкою звороту (каспом) кардіоїди) (див. рисунок).
Тоді кардіоїда має наступні рівняння:
- У декартових прямокутних координатах в неявному виді:
або
- У прямокутних координатах (параметричний запис):
також:
- Параметричні рівняння в раціональному виді:
- Параметризація в комплексній площині:
Кардіоїди у різних положеннях

При зміні положення кардіоїди в системі координат, змінюється також її рівняння. на рисунку показано деякі положення кардіоїди і відповідні їм рівняння в полярній системі координат.
Властивості
- Кардіоїда — алгебрична крива четвертого порядку.
- Кардіоїда має один простий касп, тобто особливу точку звороту 1-го роду (вістря).
- Має вісь симетрії, що проходить через касп і вершину (діаметрально протилежну точку).
- Нормаль в довільній точці кардіоїди проходить через точку дотику напрямного (нерухомого) та твірного (рухомого) кіл;
Дотична в точці проходить через точку напрямного кола, діаметрально протилежну до . Шаблон:Sfn Шаблон:Rp Шаблон:Sfn Шаблон:Rp
- Кут μ між дотичною до кардіоїди та радіус-вектором точки дотику дорівнює половині кута між цим радіус-вектором та полярною віссю: .
Кут між дотичною до кардіоїди та віссю дорівнює .
Дотичні до кардіоїди, що проведені на кінцях хорди, яка проходить через касп (вістря) кардіоїди, взаємно перпендикулярні.Шаблон:Sfn Шаблон:Rp
- При повороті на кут, кратний , кардіоїда суміщується сама з собою. Шаблон:Sfn Шаблон:Rp
- Двоїсте утворення кардіоїди.
Кардіоїда з параметрами , може бути також утворена як гіпоциклоїда (точніше перициклоїда) з параметрами .Шаблон:Sfn Шаблон:Rp Шаблон:Sfn Шаблон:Rp
Метричні характеристики
Для кардіоїди, що описана будь-яким рівнянням, представленим вище, справедливі наступні формули:Шаблон:Sfn Шаблон:Rp
- Довжина дуги повного витка кардіоїди дорівнює:
- .
Тобто довжина кардіоїди у 8 разів перевищує діаметр твірного кола.
- Довжина дуги кардіоїди від початкової точки (каспа) до довільної точки , що відповідає куту :
- .
- Площа, обмежена кардіоїдою дорівнює:
- .
Тобто площа кардіоїди в 6 разів перевищує площу твірного круга.
- Радіус кривини в точці, що відповідає полярному куту :
- Об'єм тіла, що утворене при обертанні кардіоїди навколо її осі симетрії:
- Площа поверхні цього тіла обертання:
Хорди, що проходять через касп
- C1
- Хорди , що проходять через вістря кардіоїди мають однакову довжину .
- C2
- Центри хорд, що проходять через вістря кардіоїди, лежать на нерухомому твірному колі (див. рисунок).
Кардіоїда як інверсія параболи
- Кардіоїда є інверсією (оберненою кривою) параболи з центром інверсії в її фокусі, відносно кола з цим же центром (див. рисунок).
Для прикладу, показаного на рисунку, твірне коло має радіус . Отже, кардіоїда має рівняння в полярних координатах: а її обернена крива (крива інверсії): що є рівнянням параболи; в декартовій системі координат це рівняння має вигляд: .
Заувага: Не кожна обернена крива параболи є кардіоїдою. Наприклад, якщо інверсія параболи відбудеться відносно кола, центр якого знаходиться у вершині параболи, то результатом буде цисоїда Діокла.
Кардіоїда, як обвідна для пучка кіл

Виконаємо інверсію дотичних до параболи з центром інверсії в її фокусі відносно кола з центром в цій же точці (див. попередній розділ); отримаємо пучок кіл, що проходять через центр інверсії (початок координат). При цьому центри утворених кіл лежать на нерухомому твірному колі кардіоїди. (Це коло є оберненою кривою до директриси параболи).
Ця властивість дає змогу утворити кардіоїду наступним простим методом:
- Беремо коло та фіксовану точку на ньому,
- проводимо низку кіл, що містять точку і центри яких лежать на колі ;
- обвідною цих кіл буде кардіоїда.
Кардіоїда, як обвідна пучка прямих відрізків

Схожий та простий метод утворення кардіоїди полягає у використанні пучка прямих ліній. Метод був знайдений Л. Кремоною:
- Проведемо коло і розділимо його на рівні частини точками (див. рисунок); послідовно їх пронумеруємо.
- Проведемо хорди через точки: . Тобто друга точка рухається в два рази швидше за першу.
- Обвідною цих хорд буде кардіоїда.

Заувага:
Доведення можна виконати за допомогою «умов існування обвідної» (див. попередній розділ) пучка неявно заданих кривих:
є пучком січних кола (див. вище) і
Для фіксованого параметра t обидва рівняння є рівняннями прямих. Точкою їх перетину є
яка є точкою кардіоїди з полярним рівняням
Кардіоїда як каустика кола

Міркування, зроблені у попередньому розділі, дають доказ того, що каустика кола з джерелом світла на його периметрі є кардіоїдою.
- Якщо на площині є джерело світла в точці на периметрі кола, яке відбиває будь-який промінь, то відбиті промені всередині кола є дотичними до кардіоїди.
Заувага: В подібних міркуваннях зазвичай нехтують багатократним відбиттям променя світла від дзеркальної лінії кола.
Кардіоїда як подера кола
Утворення кардіоїди методом Л. Кремони не слід плутати з наступним методом утворення кардіоїди:
Нехай дано коло та точку на ньому. Справедливо наступне твердження:
- Основи перпендикулярів, що проведені з точки на дотичні до кола є точками кардіоїди.
Отже, кардіоїда є подерою кола.

Заувага: Якщо точка не лежить на колі , отримаємо равлик Паскаля.
Еволюта кардіоїди

Еволютою кривої є геометричне місце центрів кривини.
Детальніше: для кривої з радіусом кривини еволюта має представлення
де — відповідним чином орієнтована одинична нормаль.
Для кардіоїди маємо:
- Еволюта кардіоїди — це інша кардіоїда, на третину менша за розміром і орієнтована у протилежний бік (див. рисунок).Шаблон:Sfn Шаблон:Rp Еволюта має той же центр, що і початкова кардіоїда. вершина еволюти збігається з каспом початкової кривої.Шаблон:Sfn Шаблон:Rp
Ортогональні траекторії
Ортогональними траекторіями пучка кривих є криві, що перетинають криві даного пучка під прямим кутом. Для кардіоїд справедливо наступне твердження: Шаблон:Block indent (Другий пучок є відображенням першого відносно координатної осі Oy. Див. рисунок.)
Історія
Кардіоїда вперше зустрічається в працях французького вченого Луї Карре (Louis Carrè, 1705). Назву кривій дав Джованні Сальвеміні ді Кастіллоне (Giovanni Salvemini di Castiglione, згадується також як Johann Francesco Melchiore Salvemini Castillon) 1741 року.
«Випрямлення», тобто обчислення довжини кривої, виконав Ла Ір (Philippe de La Hire), який відкрив криву незалежно 1708 року. Окрім того, незалежно описав кардіоїду голландський математик Й. Коерсма (J . Koersma, 1741). Надалі до кривої виявляли цікавість багато видатних математиків XVIII—XIX століть.
Просторова кардіоїда

Просторова кардіоїда — крива в тривимірному просторі, що має схожість з кардіоїдою. Має параметричні рівняння:[3]
Примітки
Література
Посилання
- Шаблон:Springer
- Шаблон:MathWorld
- Шаблон:MathWorld
- Шаблон:MacTutor
- Robert FERRÉOL, Cardioid, 2017
- Hearty Munching on Cardioids at cut-the-knot
- Xah Lee, Cardioid (1998) (На цьому сайті представлено кілька альтернативних конструкцій).
- Jan Wassenaar, Cardioid, (2005)
- ↑ Шаблон:MathWorld
- ↑ S Balachandra Rao . Differential Calculus, p. 457
- ↑ Шаблон:Citation