Гіпотрохоїда

Гіпотрохоїда

Гіпотрохоїда з параметрами Шаблон:Math.

Гіпотрохоїда — плоска крива, утворена фіксованою точкою, що лежить в площині деякого кола, яке котиться без ковзання по внутрішній стороні іншого нерухомого кола.

Рухоме коло називають твірним (його радіус дорівнює r), нерухоме коло — напрямним (його радіус дорівнює R).Шаблон:Sfn Шаблон:Rp

Початковою точкою гіпотрохоїди називають таку її точку $P$, що лежить на прямій, яка проходить через центр $C$ рухомого кола і його точку опори, і знаходиться по той же бік від $C$, що і точка опори.Шаблон:Sfn Шаблон:Rp

Вершиною гіпотрохоїди називають таку її точку $V$, що лежить на прямій, яка проходить через центр $C$ рухомого кола і його точку опори, і знаходиться з нею по різні боки від $C$.Шаблон:Sfn Шаблон:Rp

Будь-яка гіпотрохоїда має однакову кількість вершин і початкових точок.

Гіпотрохоїда є окремим випадком рулети — кривої, що отримана як траєкторія точки деякої кривої, що котиться без ковзання по іншій нерухомій кривій.

Граничні випадки гіпотрохоїди:

• Якщо радіус напрямного кола прямує до нескінченності ($R\to \mathrm{\infty }$), крива стає трохоїдою з тим же радіусом твірного кола.Шаблон:Sfn Шаблон:Rp
• Якщо радіус твірного кола прямує до нескінченності ($r\to \mathrm{\infty }$), твірне коло стає прямою, що котиться по нерухомому колу, а отримана крива, що описується фіксованою точкою в площині цієї прямої, є подовженою або скороченою евольвентою кола.

Рівняння

Якщо центр нерухомого кола знаходиться в початку координат, його радіус дорівнює $R$, радіус кола, що котиться по ньому дорівнює $r$, а відстань від твірної точки до центру рухомого кола дорівнює $h$, то гіпотрохоїда описується параметричними рівняннями в прямокутній системі відносно $\phi$:Шаблон:Sfn

$\{\begin{array}{c}x(\phi )=(R-r)\cos \phi +h\cdot \cos (\frac{R-r}{r}\phi )\\ y(\phi )=(R-r)\sin \phi -h\cdot \sin (\frac{R-r}{r}\phi )\end{array}\begin{array}{cc}& 0\le \phi \le 2\pi ,\text{якщо},\frac{R}{r}=k-\text{натуральне число};\\ & 0\le \phi \le 2r\cdot \pi ,\text{якщо},\frac{R}{r}=\frac{p}{q}-\text{раціональне число};\\ & 0\le \phi \le \mathrm{\infty },\text{якщо},\frac{R}{r}-\text{ірраціональне число}.\end{array}$

При цьому початкова точка гіпотрохоїди, з якої починається утворення кривої, лежить на додатній частині осі $Ox$.

Кут $\phi$ — параметр, а саме — це кут нахилу відрізка між центрами твірних кіл до осі $Ox$.

Параметричне рівняння повернутої відносно початку координат гіпотрохоїди має вигляд:

$\{\begin{array}{c}x(\phi )=(R-r)\cos \phi +h\cdot \cos (\frac{R-r}{r}\phi -\alpha )\\ y(\phi )=(R-r)\sin \phi -h\cdot \sin (\frac{R-r}{r}\phi -\alpha )\end{array}\begin{array}{cc}& \frac{r}{R}\cdot \alpha \le \phi \le 2\pi +\frac{r}{R}\cdot \alpha ,\text{якщо},\frac{R}{r}=k-\text{натуральне число};\\ & \frac{r}{R}\cdot \alpha \le \phi \le 2r\cdot \pi +\frac{r}{R}\cdot \alpha ,\text{якщо},\frac{R}{r}=\frac{p}{q}-\text{раціональне число};\\ & \frac{r}{R}\cdot \alpha \le \phi \le \mathrm{\infty },\text{якщо},\frac{R}{r}-\text{ірраціональне число}.\end{array}$

При цьому гіпотрохоїда повернута відносно початку координат проти годинникової стрілки на кут $\beta =\frac{r}{R}\cdot \alpha$ (тобто кут між відрізком, що з'єднує початкову точку гіпотрохоїди (з якої починається утворення кривої) з початком координат, та віссю $Ox$ дорівнює $\frac{r}{R}\cdot \alpha$.

Ввівши величину $k=\frac{R}{r}$, отримаємо параметричне рівняння звичайної (неповернутої) гіпотрохоїди у вигляді:

$\{\begin{array}{cc}& x(\phi )=r\cdot (k-1)\cos \phi +h\cdot \cos ((k-1)\phi )\\ & y(\phi )=r\cdot (k-1)\sin \phi -h\cdot \sin ((k-1)\phi )\end{array}$

де $R$ — радіус нерухомого кола,
$r$ — радіус кола, що котиться,
$h$ — відстань від твірної точки до центра рухомого кола.

Величина $k$ визначає форму гіпотрохоїди (див. нижче).

Ці рівняння можна записати більш компактно у комплексній формі:

$z(\phi )=r\cdot (k-1)e^{i\phi }+h\cdot e^{-i(k-1)\phi }$ .

де

• кут $\phi \in [0,2\pi ]$ ;
• радіус твірного (рухомого) кола $r$;
• радіус напрямного (нерухомого) кола $R=kr$;
• відстань від твірної точки до центра рухомого кола $h$.

Властивості та особливості форми

• Будь-яка гіпотрохоїда лежить в круговому кільці, обмеженому колами з радіусами $|R-r-h|$ та $|R-r+h|$.
  

На першому з них лежать вершини, а на другому — початкові точки гіпотрохоїди.

• При повороті навколо початку координат (центру нерухомого кола) $O$ на кут, кратний $2\pi \cdot \frac{r}{R}$, гіпотрохоїда суміщається сама з собою.Шаблон:Sfn Шаблон:Rp
• Якщо $k=\frac{R}{r}$ — натуральне число, то гіпотрохоїда є замкненою алгебричною кривою $2(k-1)$ порядку;
  

Крива складається з $k$ конгруентних гілок, а отже, має $k$ вершин та початкових точок.

При цьому твірне коло, що обертається навколо нерухомого кола, робить $(k-1)$ повних обертів навколо свого центру.

• Якщо $k=\frac{R}{r}=\frac{p}{q}$ — раціональне число, виражене у вигляді нескоротного дробу, то гіпотрохоїда є замкненою алгебричною кривою $2\cdot |p-q|$ порядку;
  

Крива складається з $p$ конгруентних гілок, а отже, має $p$ вершин та початкових точок.

При цьому твірне коло, що обертається навколо нерухомого кола, робить $|p-q|$ повних обертів навколо свого центру.

• Якщо $k$ — ірраціональне число, то гіпотрохоїда є незамкненою кривою, та має нескінченну кількість гілок, вершин та каспів. При необмеженому збільшенні параметра $\phi$, крива щільно заповнює кільце, обмежене колами з радіусами $|R-r-h|$ та $|R-r+h|$.
• Гіпотрохоїда має однакову кількість вершин та каспів;
• Гіпотрохоїду з параметрами $(R,r,h)$ можна отримати так само як гіпотрохоїду з параметрами.Шаблон:Sfn Шаблон:Rp

$R_1=\frac{h}{r}\cdot R;r_1=\frac{h}{r}\cdot (R-r);h_1=R-r$.

У випадку, коли $R<r$, крива $(R_1,r_1,h_1)$ є епітрохоїдою з параметрами

$R_1=\frac{h}{r}\cdot R;r_1=\frac{h}{r}\cdot (r-R);h_1=r-R$.

Заувага: Гіпотрохоїда, яка при одному способі утворення, була подовженою, при іншому способі утворення виявляється скороченою (і навпаки).

• Властивість нормалі

Нормаль, що проведена через будь-яку точку $M$ гіпотрохоїди, проходить через відповідну точку дотику $E$ твірного (рухомого) та напрямного (нерухомого) кіл.Шаблон:Sfn Шаблон:Rp

Метричні характеристики

• Довжина дуги гіпотрохоїди між точками, що відповідають кутам $0\le \phi \le {\phi }_1$: Шаблон:Sfn Шаблон:Rp

$\ell =\left|\frac{R-r}{r}\right|\cdot \underset{0}{\overset{{\phi }_1}{\int }}\sqrt{r^2+h^2-2rh\cdot \cos (\frac{R}{2r}\cdot \phi )}d\phi$

Ця дуга по довжині дорівнює довжині еліпса

$\{\begin{array}{cc}& x(\phi )=2(h-r)\cdot \frac{R-r}{R}\cdot \cos (\frac{R}{2r}\cdot \phi )\\ & y(\phi )=2(h+r)\cdot \frac{R-r}{R}\cdot \sin (\frac{R}{2r}\cdot \phi )\end{array}$

між точками з тими ж значеннями кута $\phi$.

Інтеграл в загальному випадку не виражається через елементарні функції, але у випадках, коли гіпотрохоїда є гіпоциклоїдою, його можна виразити в елементарних функціях.

Також довжину дуги гіпотрохоїди від її початку до точки, що відповідає параметру $\phi$ можна обчислити за формулою:

$\ell (\phi )=2\cdot |(R-r)(r-h)|\cdot E(\frac{R}{2r}\cdot \phi ;\frac{2i\cdot \sqrt{rh}}{|r-h|})$

де $E(x;m)$ — еліптичний інтеграл другого роду.

• Площа сектора, що описується полярним радіусом $OM$ гіпотрохоїди, коли точка $M$ пробігає по дузі між точками, що відповідають кутам $0\le \phi \le {\phi }_1$: Шаблон:Sfn Шаблон:Rp

$S=\frac{(R-r)}{2}\cdot ((R-r-\frac{h^2}{r})\cdot {\phi }_1+\frac{h(R-2r)}{R}\cdot \sin (\frac{R}{r}\cdot {\phi }_1)).$

Тут площа розглядається як спрямована величина, тобто приймається, що в тих проміжках зміни параметра $\phi$, де полярний радіус обертається у від'ємному напрямку, він описує від'ємну площу.Шаблон:Sfn Шаблон:Rp

• Радіус кривини будь-якої гіпотрохоїди в деякій її точці $M$, що відповідає куту $\phi$Шаблон:Sfn Шаблон:Rp:

$\rho =(R-r)\cdot \frac{{(r^2+h^2-2rh\cdot \cos (\frac{R}{r}\cdot \phi ))}^{3/2}}{|r^3-h^2(R-r)+rh(R-2r)\cdot \cos (\frac{R}{r}\cdot \phi )|}$

Окремі випадки

Окремими випадками гіпотрохоїди є:

• Гіпоциклоїда (коли точка, що її утворює, лежить на самому твірному колі, тобто при $h=r$);
• Еліпс з центром в початку координат (при параметрах $R=2r;h\ne r$).

Напіввісі цього еліпса дорівнюють: $a=r+h;b=|r-h|$; кінцями великої осі є початкові точки гіпотрохоїди, кінцями малої осі — її вершини.

Ексцентриситет цього еліпса:

$e=\frac{2\sqrt{h/r}}{1+(h/r)}$

Еліпс (червона лінія) може бути представлений як окремий випадок гіпотрохоїди з параметрами Шаблон:Math (Tusi couple); на цьому рисунку Шаблон:Math.

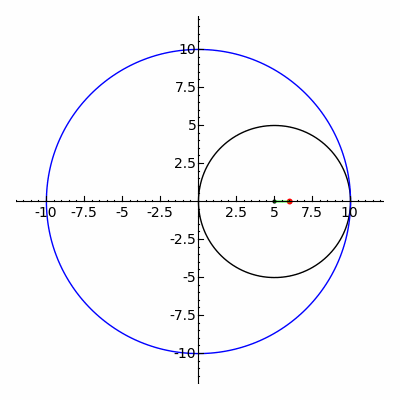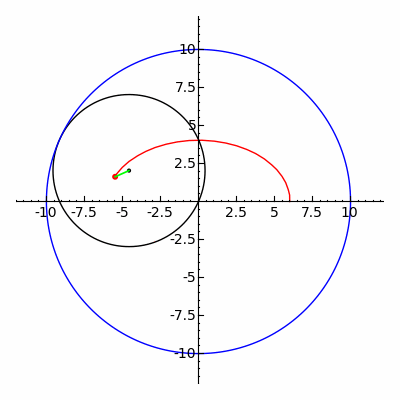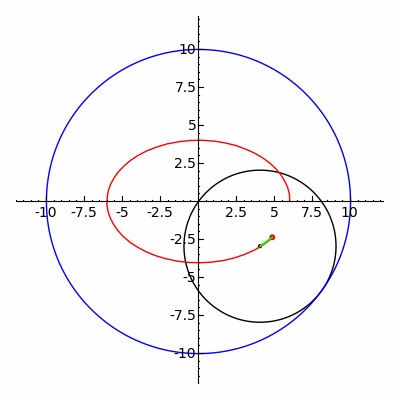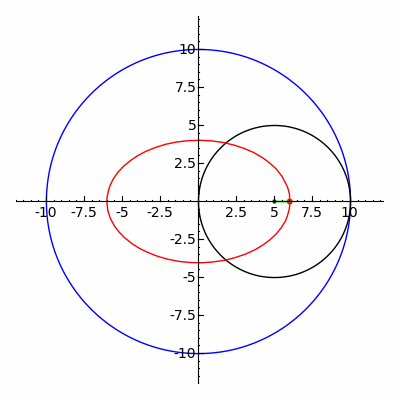
Якщо за сталих $R$ та $r$, що пов'язані співвідношенням $R=2r$, різниця $r-h$ прямує до нуля, то мала вісь еліпса необмежено зменшується, а велика наближається до діаметра напрямного кола. Звичайна гіпоциклоїда, що утворюється в граничному випадку ($r=h$), являє собою відрізок прямої, а саме той діаметр напрямного кола, що з'єднує початкові точки.

• Троянда з індексом $n>1$ (при $h=R-r$).

Початок координат є вузловою точкою.

Рівняння кривої в полярних координатах має вигляд:

$\rho =2h\cdot \cos (\frac{k}{k-2}\cdot \theta )$

Цікаві факти

• Логотип Adobe Acrobat являє собою дещо деформовану гіпотрохоїду.

Див. також

• Рулета
• Трохоїда
• Епітрохоїда
• Спірограф — дитяча іграшка, яка дозволяє малювати гіпотрохоїди.

Література

• Шаблон:Cite book

• Шаблон:Книга

• Шаблон:КнигаШаблон:Ref-ru

Посилання

• Шаблон:MathWorld
• Шаблон:Springer
• Шаблон:MacTutor
• Robert FERRÉOL, Jacques MANDONNET Гіпотрохоїда на сайті [Mathcurve] , 2017