Ін'єктивний об'єкт

Ін'єктивний об'єкт — теоретико-категорне узагальнення поняття ін'єктивних модулів. Двоїстим є поняття проєктивного об'єкта.

Означення

Об'єкт Шаблон:Var є ін'єктивним, якщо для мономорфізму Шаблон:Var : Шаблон:Var → Шаблон:Var, довільний морфізм Шаблон:Var : Шаблон:Var → Шаблон:Var можна продовжити до Шаблон:Var.

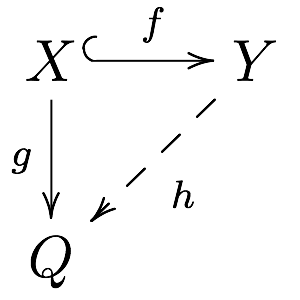
Об'єкт $Q$ категорії $C$ називається ін'єктивним, якщо для будь-якого морфізма $g:X\to Q$ і будь-якого мономорфізма $f:X\to Y$ існує (не обов'язково єдиний) морфізм $h:Y\to Q,$для якого $h\circ f=g$.

У локально малих категоріях, об'єкт $Q$ є ін'єктивним тоді і тільки тоді коли контраваріантний функтор Hom ${\mathrm{Hom}}_{ℭ}(-,Q)$ переводить мономорфізми у $ℭ$ у сюр'єктивні відображення множин.

Досить багато ін'єктивних об'єктів

Кажуть, що в категорії $C$ досить багато ін'єктивних об'єктів, якщо для будь-якого об'єкта $X$ категорії $C$ існує мономорфізм $f:X\to Q$ в ін'єктивний об'єкт $Q$.

Ін'єктивна оболонка

Шаблон:Докладніше Мономорфізм $g$ категорії $C$ називається істотним, якщо для будь-якого морфізма $f$ композиція $f\circ g$ є мономорфізмом, тільки якщо $f$ є мономорфізмом.

Якщо $f:X\to G$ — істотний мономорфізм і об'єкт $G$ є ін'єктивним, то $G$ називається ін'єктивною оболонкою $X$. Ін'єктивна оболонка є єдиною з точністю до неканонічного ізоморфізму.

Випадок абелевих категорій

Якщо $𝒞$ — (локально мала) абелева категорія, то її об'єкт $Q$ називається ін'єктивним тоді і тільки тоді, коли функтор Hom ${\mathrm{H}\mathrm{o}\mathrm{m}}_{𝒞}(-,Q)$ є точним.

Ще одним еквівалентним еквівалентним означенням є: об'єкт $Q$ є ін'єктивним якщо і тільки якщо кожна послідовність виду

$0\to Q\to U\to V\to 0$

є точною у $𝒞$ тоді і тільки тоді коли вона розщеплюється, тобто $U$ є ізоморфним прямій сумі $Q\oplus V$.

Загалом контраваріантний функтор Hom є точним зліва, тобто для короткої точної послідовності $0\to A\to B\to C\to 0$ точною є лише послідовність $0\to \mathrm{H}\mathrm{o}\mathrm{m}(C,Q)\to \mathrm{H}\mathrm{o}\mathrm{m}(B,Q)\to \mathrm{H}\mathrm{o}\mathrm{m}(A,Q).$ Для того щоб цей функтор був точним необхідно і достатньо щоб відображення $\mathrm{H}\mathrm{o}\mathrm{m}(B,Q)\to \mathrm{H}\mathrm{o}\mathrm{m}(A,Q)$ було сюр'єктивним, тобто для кожного морфізма $f:A\to Q$ існував морфізм $g:B\to Q,$ для якого $g\circ h=f,$ де $h:A\to B$ — морфізм із початкової точної послідовності. Оскільки в абелевій категорії мономорфізм $h:A\to B$ завжди можна продовжити до короткої точної послідовності (взявши за C коядро h) то звідси одержується еквівалентність загального означення із означенням через точність функтора Hom.

Якщо $Q$ є ін'єктивним об'єктом і $\mathrm{Id}:Q\to Q$ — одиничний морфізм, то з означення ін'єктивності випливає, що для мономорфізма $h:Q\to U$ існує морфізм $g:U\to Q,$ такий що ${\mathrm{Id}}_Q=h\circ g.$ Але існування такого морфізма є еквівалентним розщепленню точної послідовності $0\to Q\to U\to V\to 0.$

Навпаки, нехай довільна така коротка точна послідовність розщеплюється, $h:A\to B$ — мономорфізм і $f:A\to Q$ — довільний морфізм. В абелевій категорії існують всі розшаровані кодобутки і існування морфізму $g:B\to Q,$ для якого $g\circ h=f$ є еквівалентним існуванню морфізма $\overline{g}:B{\bigsqcup }_{A}Q\to Q,$ для якого ${\mathrm{Id}}_Q=\overline{g}\circ i_2.$ У абелевій категорії розшаровані кодобутки зберігають мономорфізми, тому $i_2:Q\to B{\bigsqcup }_{A}Q$ теж є мономорфізмом і тому частиною точної послідовності :$0\to Q\to B{\bigsqcup }_{A}Q\to \mathrm{Kocer}{i}_2\to 0.$ Оскільки згідно умови ця послідовність розщеплюється то необхідний морфізм $\overline{g}$ існує.

Як і кожен контраваріантний адитивний функтор ${\mathrm{H}\mathrm{o}\mathrm{m}}_C(-,Q)$ є точним справа тоді і тільки тоді, коли переводить ядра у коядра. Ця умова є ще одною еквівалентною умовою ін'єктивності об'єкта $Q.$

Властивості

• Нехай $Q=\prod _{i\in I}{Q}_i$ — добуток деякої сім'ї об'єктів. Тоді $Q$ є ін'єктивним тоді і тільки тоді, коли всі $Q_i$ є ін'єктивними.
• Будь-який ін'єктивний підоб'єкт $Q$ об'єкта $C$ є його прямим доданком.
• Якщо ${𝒞}_1,{𝒞}_2$ — абелеві категорії і $G:{𝒞}_2\to {𝒞}_1$ — функтор спряжений до точного функтора $F:{𝒞}_1\to {𝒞}_2,$ то G переводить ін'єктивні об'єкти категорії ${𝒞}_2$ у ін'єктивні об'єкти категорії ${𝒞}_1.$
• Нехай ${𝒞}_1,{𝒞}_2$ — абелеві категорії і $G:{𝒞}_2\to {𝒞}_1$ — функтор спряжений справа до функтора $F:{𝒞}_1\to {𝒞}_2.$ Якщо G переводить ін'єктивні об'єкти категорії ${𝒞}_2$ у ін'єктивні об'єкти категорії ${𝒞}_1$ і у ${𝒞}_2$ є досить багато ін'єктивних об'єктів, то F є точним функтором.
• Якщо $Q_1,Q_2$ є ін'єктивними оболонками об'єктів $P_1,P_2$ відповідно, то $Q_1\oplus Q_2$ є ін'єктивною оболонкою $P_1\oplus P_2.$
• Якщо $Q_1,Q_2$ є ін'єктивними оболонками об'єкта $P,$ то вони є ізоморфними.

Приклади

• У категорії абелевих груп ін'єктивними об'єктами є подільні групи.
• Адитивна група раціональних чисел є ін'єктивною оболонкою адитивної групи цілих чисел у категорії абелевих груп.
• Нехай p — просте число. Нехай $Z_{p^{\mathrm{\infty }}}$ — мультиплікативна підгрупа комплексних чисел, що задовольняють хоча б одному рівнянню виду $z^{p^n}=1,n>0.$ Тоді у категорії абелевих груп $Z_{p^{\mathrm{\infty }}}$ є ін'єктивною оболонкою для всіх груп $Z_{p^m}$ — коренів з одиниці степеня $p^m.$
• У категорії модулів $R-\mathrm{M}\mathrm{o}\mathrm{d}$ ін'єктивними об'єктами є ін'єктивні модулі. У $R-\mathrm{M}\mathrm{o}\mathrm{d}$ існують ін'єктивні оболонки, і, як наслідок, досить багато ін'єктивних об'єктів.
• В категорії метричних просторів і коротких відображень ін'єктивними об'єктами є ін'єктивні метричні простори.
• Розглядають також ін'єктивні об'єкти в більш загальних категоріях, наприклад в категоріях функторів або в категоріях пучків модулів.

Узагальнення

об'єкт Шаблон:Var є Шаблон:Var-ін'єктивним якщо для Шаблон:Var : Шаблон:Var → Шаблон:Var із класу Шаблон:Var, для будь-якого Шаблон:Var : Шаблон:Var → Шаблон:Var існує комутативна діаграма.

Нехай $ℭ$ є категорією і $\mathscr{H}$ — клас морфізмів у $ℭ$.

Об'єкт $Q$ категорії $ℭ$ називається $\mathscr{H}$-ін'єктивним якщо для будь-якого морфізма $f:\to Q$ і кожного морфізма $h:\to B$ з класу $\mathscr{H}$ існує морфізм $g:B\to Q$ для якого $g\circ h=f$.

Якщо $\mathscr{H}$ є класом мономорфізмів то одержується означення ін'єктивних модулів.

Категорія $ℭ$ має досить багато $\mathscr{H}$-ін'єктивних об'єктів якщо для кожного об'єкта X категорії $ℭ$, існує $\mathscr{H}$-морфізм із X у $\mathscr{H}$-ін'єктивний об'єкт.

$\mathscr{H}$-морфізм g у $ℭ$ називається $\mathscr{H}$-істотним якщо для будь-якого морфізма f, композиція fg належить класу $\mathscr{H}$ лише якщо f належить класу $\mathscr{H}$.

Якщо g є $\mathscr{H}$-істотним морфізмом із X у $\mathscr{H}$-ін'єктивний об'єкт G, то G називається H-ін'єктивною оболонкою об'єкта X.

Див. також

• Ін'єктивний модуль
• Проєктивний об'єкт

Література

• И. Букур, А. Деляну Введение в теорию категорий и функторов. — М.: Мир, 1972.
• Шаблон:Citation