Теорема синусів

Шаблон:Тригонометрія Теорема синусів — наступне тригонометричне твердження про властивості кутів та сторін довільного трикутника: нехай a, b і c є сторонами трикутника, а A, B і C — кути протилежні вказаним сторонам, тоді

$\frac{\sin A}{a}=\frac{\sin B}{b}=\frac{\sin C}{c}$

Обернене значення числа в теоремі синусів (тобто a/sin(A)) дорівнює діаметру D (або ж 2-ом радіусам) описаного навколо трикутника кола (єдине коло, що проходить через три точки A, B і C). Таким чином теорему можна переписати у розширеній формі

$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=D=2R$

Наслідком теореми синусів є наступне твердження:

• У трикутнику навпроти більшого кута лежить більша сторона, навпроти більшої сторони лежить більший кут.

Розв'язання трикутників

Теорему синусів використовують при розв'язуванні трикутників:

1. Якщо відомі сторона Шаблон:Math та два прилеглі кути Шаблон:Math і Шаблон:Math довільного трикутника, то інші дві сторони можемо знайти із співвідношення:

$b=a\cdot \frac{\sin \beta }{\sin \alpha }=a\cdot \frac{\sin \beta }{\sin (\pi -\beta -\gamma )}$;

$c=a\cdot \frac{\sin \gamma }{\sin \alpha }=a\cdot \frac{\sin \gamma }{\sin (\pi -\beta -\gamma )}$.

Це є типовою проблемою, що постає при тріангуляції.

2. Якщо відомі дві сторони та один із кутів, що не утворюється цими сторонами

Зазначена формула дає два можливих значення для внутрішнього кута. В цьому випадку, часто лишень одне значення задовольняє умові, що сума трьох кутів трикутника дорівнює 180°; інакше отримаємо два можливих розв'язки.

Доведення

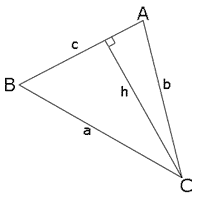
Нехай дано трикутник зі сторонами a, b, і c, з протилежними до них кутами A, B, і C. Опустимо перпендикуляр довжиною h з C на c.

Бачимо, що, за означенням:

$\sin A=\frac{h}{b}$ та $\sin B=\frac{h}{a}$

Звідси:

$h=b\sin A=a\sin B$

також

$\frac{\sin A}{a}=\frac{\sin B}{b}$

Повторимо операцію з кутом A і стороною a, і дістанемо:

$\frac{\sin B}{b}=\frac{\sin C}{c}$.∎

Доведення розширеної форми теореми синусів

Достатньо довести, що

$\frac{a}{\sin \alpha }=2R.$

Проведемо діаметр $|BG|$ описаного кола.

За властивістю кутів, вписаних у коло, кут $GCB$ прямий, а кут $CGB$ дорівнює або $\alpha$, якщо точки $A$ і $G$ лежать по один бік від прямої $BC$, або $\pi -\alpha$ в іншому разі.

Оскільки $\sin (\pi -\alpha )=\sin \alpha$, в обох випадках маємо

$a=2R\sin \alpha$.

Повторивши ці міркування для двох інших сторін трикутника, маємо:

$\frac{a}{\sin \alpha }=\frac{b}{\sin \beta }=\frac{c}{\sin \gamma }=2R.$ ∎

Варіації та узагальнення

• У симплексі

$V_n=\frac{n-1}{n}\cdot \frac{V_{n-1}^i{V}_{n-1}^j}{V_{n-2}^{i,j}}\cdot \sin A_{i,j},$

де $A_{i,j}$ — кут між гранями $V_{n-1}^i$ і $V_{n-1}^j$; $V_{n-2}^{i,j}$ — спільна грань $V_{n-1}^i$ і $V_{n-1}^j$; $V_n$ — об'єм симплекса.

Теорема синусів для сферичного трикутника

Шаблон:Докладніше Ця теорема справедлива для трикутників на сфері, сторонами яких є дуги великих кіл сфери.

Нехай дано сферу одиничного радіуса і трикутник на ній, утворений перетином трьох її великих кіл. Нехай Шаблон:Math, Шаблон:Math і Шаблон:Math — довжини дуг, які є сторонами трикутника. Оскільки сфера є одиничною, то Шаблон:Math, Шаблон:Math і Шаблон:Math виражають кути з вершиною у центрі сфери між двома її радіусами, стягнуті цими дугами в радіанах.

Нехай Шаблон:Math, Шаблон:Math і Шаблон:Math — кути, протилежні цим сторонам, тобто це двогранні кути між площинами трьох великих кіл.

Тоді, для сферичного трикутника справедливе твердження: $$\frac{\sin A}{\sin a}=\frac{\sin B}{\sin b}=\frac{\sin C}{\sin c}.$$

Доведення через вектори

Розглянемо сферу одиничного радіуса з центром О в початку координат. Шаблон:Math, Шаблон:Math та Шаблон:Math — одиничні вектори, проведені від початку координат до вершин Шаблон:Math, Шаблон:Math, Шаблон:Math трикутника. Отже, кути Шаблон:Math, Шаблон:Math і Шаблон:Math є кутами Шаблон:Math, Шаблон:Math і Шаблон:Math відповідно. Дуга Шаблон:Math утворює кут величиною Шаблон:Math з вершиною у центрі сфери.

Введемо декартову систему координат так, щоб її вісь Шаблон:Math проходила вздовж вектора Шаблон:Math. Вектор Шаблон:Math в площині Шаблон:Math утворює кут утворює кут Шаблон:Math з віссю Шаблон:Math та проектується на відрізок Шаблон:Math у площині Шаблон:Math. Вектор Шаблон:Math утворює кут Шаблон:Math з віссю Шаблон:Math та проектується на Шаблон:Math у площині Шаблон:Math, а кут між Шаблон:Math та віссю Шаблон:Math дорівнює Шаблон:Math. Отже, три вектори мають координати:

$$𝐎𝐀=\left(\begin{array}{c}0\\ 0\\ 1\end{array}\right),𝐎𝐁=\left(\begin{array}{c}\sin c\\ 0\\ \cos c\end{array}\right),𝐎𝐂=\left(\begin{array}{c}\sin b\cos A\\ \sin b\sin A\\ \cos b\end{array}\right).$$

Змішаний добуток трьох векторів, Шаблон:Math, дорівнює об'єму паралелепіпеда, побудованого на векторах Шаблон:Math, Шаблон:Math та Шаблон:Math. Цей об'єм є інваріантним до конкретної системи координат, яка використовується для представлення Шаблон:Math, Шаблон:Math і Шаблон:Math.

Значення змішаного добутку трьох векторів Шаблон:Math є Шаблон:Math — визначником, рядками якого є координати векторів Шаблон:Math, Шаблон:Math і Шаблон:Math.

З віссю Шаблон:Math вздовж Шаблон:Math квадрат цього визначника дорівнює

$$\begin{array}{cc}(𝐎𝐀\cdot (𝐎𝐁\times 𝐎𝐂){)}^2& ={(\det \left(\begin{array}{ccc}𝐎𝐀& 𝐎𝐁& 𝐎𝐂\end{array}\right))}^2\\ & ={\left|\begin{array}{ccc}0& 0& 1\\ \sin c& 0& \cos c\\ \sin b\cos A& \sin b\sin A& \cos b\end{array}\right|}^2={(\sin b\sin c\sin A)}^2.\end{array}$$

Якщо повторити це обчислення з віссю Шаблон:Math вздовж Шаблон:Math, отримаємо Шаблон:Math, а з віссю Шаблон:Math вздовж Шаблон:Math — Шаблон:Math.

Прирівнюємо ці вирази та ділимо їх на Шаблон:Math: $$\frac{{\sin }^{2}A}{{\sin }^{2}a}=\frac{{\sin }^{2}B}{{\sin }^{2}b}=\frac{{\sin }^{2}C}{{\sin }^{2}c}=\frac{V^2}{{\sin }^2(a){\sin }^2(b){\sin }^2(c)},$$ де Шаблон:Mvar — об'єм паралелепіпеда, побудованого на векторах Шаблон:Math, Шаблон:Math та Шаблон:Math, що відповідають вершинам сферичного трикутника.

Легко побачити, що для малих сферичних трикутників, коли радіус сфери значно перевищує довжини сторін трикутника, ця формула в граничному значенні переходить в формулу для плоского трикутника, оскільки

$$\underset{a\to 0}{\lim }\frac{\sin a}{a}=1$$ і так само для Шаблон:Math та Шаблон:Math.

Доведення геометричне

Розглянемо сферу одиничного радіуса: $$OA=OB=OC=1$$

Будуємо точку $D$ та точку $E$ так, що $\mathrm{\angle }ADO=\mathrm{\angle }AEO=90^{\circ }$

Будуємо точку $A^{\prime }$ так, що $\mathrm{\angle }{A}^{\prime }DO=\mathrm{\angle }{A}^{\prime }EO=90^{\circ }$

Тому видно, що $\mathrm{\angle }AD{A}^{\prime }=B$ та $\mathrm{\angle }AE{A}^{\prime }=C$

Точка $A^{\prime }$ є проекцією точки $A$ на площину $OBC$. Тому $\mathrm{\angle }A{A}^{\prime }D=\mathrm{\angle }A{A}^{\prime }E=90^{\circ }$

Згідно з основною тригонометрією, маємо: $$\begin{array}{cc}AD& =\sin c\\ AE& =\sin b\end{array}$$

Але $A{A}^{\prime }=AD\cdot \sin B=AE\cdot \sin C$

Поєднавши ці рівності, отримаємо: $$\begin{array}{cc}\sin c\cdot \sin B& =\sin b\cdot \sin C\\ \Rightarrow \frac{\sin B}{\sin b}& =\frac{\sin C}{\sin c}\end{array}$$

Проводячи аналогічні обчислення, отримуємо теорему синусів для сферичного трикутника: $$\frac{\sin A}{\sin a}=\frac{\sin B}{\sin b}=\frac{\sin C}{\sin c}$$

Малюнок, використаний в геометричному доказі вище, використовується і також надається в (див. Малюнок 3 у цьому документі) для виведення теореми синусів за допомогою елементарної лінійної алгебри та проекційних матриць.

Теорема синусів для гіперболічного трикутника

У гіперболічній геометрії з кривиною −1, теорема синусів для гіперболічного трикутника має вигляд:

$$\frac{\sin A}{\mathrm{s}\mathrm{h}a}=\frac{\sin B}{\mathrm{s}\mathrm{h}b}=\frac{\sin C}{\mathrm{s}\mathrm{h}c},$$

В окремому випадку, коли кут Шаблон:Math прямий, отримаємо: $$\sin C=\frac{\sinh c}{\sinh b}$$

що є аналогом формули в евклідовій геометрії, яка виражає синус кута як частку від ділення протилежної сторони прямокутного трикутника на його гіпотенузу.

Теорема синусів для поверхонь постійної кривини

Визначимо узагальнену функцію синусів, що залежить також від дійсного параметра Шаблон:Math: $${\sin }_{K}x=x-\frac{K{x}^3}{3!}+\frac{K^2{x}^5}{5!}-\frac{K^3{x}^7}{7!}+\cdots .$$

Теорема синусів при постійній кривині Шаблон:Math має вигляд $$\frac{\sin A}{{\sin }_{K}a}=\frac{\sin B}{{\sin }_{K}b}=\frac{\sin C}{{\sin }_{K}c}.$$

Підставивши Шаблон:Math, Шаблон:Math, або Шаблон:Math, Отримаємо відповідно евклідовий, сферичний та гіперболічний випадки теореми синусів, описані вище.

Нехай Шаблон:Math позначає довжину кола радіуса Шаблон:Math у просторі постійної кривини Шаблон:Math.

Тоді Шаблон:Math.

Тому теорему синусів також можна записати у вигляді: $$\frac{\sin A}{p_K(a)}=\frac{\sin B}{p_K(b)}=\frac{\sin C}{p_K(c)}.$$

Це формулювання було знайдене Яношом Бояї.

У вищих розмірностях

• у тривімірному просторі тетраедр має чотири трикутних граней. Абсолютне значення Шаблон:Не перекладено (psin) нормальних векторів до трьох граней, що мають спільну вершину тетраедра, поділене на площу четвертої грані, не залежить від вибору вершини:

$$\begin{array}{cc}& \frac{|\mathrm{psin}(𝐛,𝐜,𝐝)|}{{\mathrm{S}}_a}=\frac{|\mathrm{psin}(𝐚,𝐜,𝐝)|}{{\mathrm{S}}_b}=\frac{|\mathrm{psin}(𝐚,𝐛,𝐝)|}{{\mathrm{S}}_c}=\frac{|\mathrm{psin}(𝐚,𝐛,𝐜)|}{{\mathrm{S}}_d}\\ =& \frac{(3{\mathrm{V}}_{\text{тетр.}}{)}^2}{2!{\mathrm{S}}_a\cdot {\mathrm{S}}_b\cdot {\mathrm{S}}_c\cdot {\mathrm{S}}_d}.\end{array}$$

• Для Шаблон:Math — вимірного симплекса (тобто, трикутника (Шаблон:Math), тетраедра (Шаблон:Math), п'ятикомірника (Шаблон:Math), тощо) в Шаблон:Math — вимірному евклідовому просторі, абсолютна величина Шаблон:Не перекладено нормальних векторів до фасетів, що мають спільну вершину, поділена на гіперплощу грані, протилежної до цієї вершини, не залежить від вибору вершини.

Позначимо Шаблон:Math — гіпероб'єм Шаблон:Math-вимірного симплекса і Шаблон:Math — добуток гіперплощ його Шаблон:Math-вимірних граней. Тоді загальне співвідношення має вигляд

$$\frac{|\mathrm{psin}(𝐛,\dots ,𝐳)|}{{\mathrm{S}}_a}=\cdots =\frac{|\mathrm{psin}(𝐚,\dots ,𝐲)|}{{\mathrm{S}}_z}=\frac{(nV{)}^{n-1}}{(n-1)!P}.$$

Історія

У першій главі Альмагеста (бл. 140 року н. е.) теорему синусів використано, але явно не сформульовано.

Найдавніше з доведень, що дійшли до нас, теореми синусів на площині описано в книзі Насир ад-Діна ат-Тусі «Трактат про повний чотирибічник» написаній у XIII столітті.

Теорему синусів для сферичного трикутника довели математики середньовічного Сходу ще в X столітті. У праці Шаблон:Нп XI століття «Книга про невідомі дуги сфери» наводилось загальне доведення теореми синусів на сфері.

Див. також

• Тріангуляція
• Теорема косинусів
• Теорема тангенсів
• Теорема котангенсів

Посилання

• Шаблон:УСЕ-4
• Теорема синусів: формулювання та доведення
• Шаблон:MathWorld