Теорія категорій

Теорія категорій — розділ математики, що вивчає властивості відношень між математичними структурами, незалежно від внутрішньої будови структур; абстрагується від множин та функцій до діаграм, де об'єкти сполучені морфізмами (стрілками).

Теорія категорій посідає центральне місце в сучасній математиці, а також має застосування в інформатиці та теоретичній фізиці. Сучасне викладання алгебричної геометрії та гомологічної алгебри основане на теорії категорії. Поняття теорії категорій використане в мові функційного програмування Haskell.

Історія

Поняття категорія було введено в 1945 році. Своїм походженням теорія категорій завдячує алгебраїчній топології. Подальші дослідження виявили об'єднувальну та уніфікувальну роль поняття категорія і пов'язаного з ним поняття функтора для багатьох розділів математики.

Теоретико-категорний аналіз основ теорії гомології привів до виділення у середині 50-х рр. 20 ст. так званих абелевих категорій, в рамках яких виявилося можливим здійснити основні побудови гомологічної алгебри. У 60-і рр. 20 ст. позначилася дедалі більша цікавість до неабелевих категорій, спонуканий задачами логіки, загальної алгебри, топології і алгебраїчної геометрії. Інтенсивний розвиток універсальної алгебри і аксіоматична побудова теорії гомотопій поклали початок різним напрямам досліджень: категорному дослідженню многовидів універсальної алгебри, теорії ізоморфізмів прямих розкладів, теорії зв'язаних функторів і теорії двоїстості функторів. Подальший розвиток виявив істотний взаємозв'язок між цими дослідженнями. Завдяки виникненню теорії відносних категорій, що широко використовує техніку зв'язаних функторів і замкнутих категорій, була встановлена двоїстість між теорією гомотопій і теорією універсальних алгебр, заснована на інтерпретації категорних визначень моноїда і комоноїда у відповідних функторів. Інший спосіб введення додаткових структур в категоріях пов'язаний із заданням в категоріях топології і побудові категорії пучків над топологічною категорією (так зв. топоси).

Визначення

Категорія

Категорія $𝒞$ складається з класу ${\text{Ob}}_{𝒞}$, елементи якого називаються об'єктами категорії, та класу ${\text{Mor}}_{𝒞}$, елементи якого називаються морфізмами категорії. Ці класи повинні задовольняти такі умови:

1. Кожній впорядкованій парі об'єктів А, В зіставлено клас ${\text{Hom}}_{𝒞}(A,B)$; якщо $f\in {\text{Hom}}_{𝒞}(A,B)$, то А називається початком, або областю визначення морфізму f, а В — кінець, або область значень f.
2. Кожен морфізм категорії належить одному і лише одному класу ${\text{Hom}}_{𝒞}(A,B)$.
3. У класі $Mo{r}_{𝒞}$ заданий частковий закон множення: добуток морфізмів $f\in \text{Hom}(A,B)$ та $g\in \text{Hom}(C,D)$ визначено тоді і тільки тоді, коли В=С, він позначається $g\circ f$ і належить класу $\text{Hom}(A,D)$.
4. Справедливий закон асоціативності: $h\circ (g\circ f)=(h\circ g)\circ f$ для будь-яких морфізмів, для яких дані добутки визначені.
5. У кожному класі $\text{Hom}(A,A)$ визначений такий морфізм $i{d}_A$, що $f\circ i{d}_A=i{d}_B\circ f=f$ для $f\in \text{Hom}(A,B)$; морфізми $i{d}_A$ називаються одиничними, тотожними, або одиницями.

Замітка: клас об'єктів звичайно не є множиною в сенсі аксіоматичної теорії множин. Категорія, в якій об'єкти складають множину, називається малою. Крім того, у принципі можливо (з невеликим виправленням визначення) розглядати категорії, в яких морфізми між будь-якими двома об'єктами також утворюють клас, або навіть велику структуру.

Приклади категорій

• Set — категорія множин. Об'єктами є множини, морфізмами — відображення множин, а множення збігається з послідовним виконанням відображень.
• Top — категорія топологічних просторів. Об'єктами є топологічні простори, морфізмами — всі неперервні відображення топологічних просторів, а множення знову збігається з послідовним виконанням відображень.
• Group — категорія груп. Об'єктами є групи, морфізмами — всі гомоморфізми груп, а множення збігається з послідовним виконанням гомоморфізмів. За аналогією можна ввести категорію кілець і т. д.
• Vect_K — категорія векторних просторів над полем K. Морфізми — лінійні відображення векторних просторів.
• Rel — категорія бінарних відношень множини; клас об'єктів цієї категорії збігається з класом об'єктів Set, а морфізмами множини А в множину В є бінарні відношення цих множин, тобто всілякі підмножини декартового добутку А×В; множення збігається з множенням бінарних відношень.
• Моноїд є категорією з одним об'єктом, навпаки, кожна категорія, що складається з одного об'єкта, є моноїдом.
• Для будь-якої частково впорядкованої множини можна побудувати малу категорію, об'єктами якої є елементи множини, причому між елементами x і y існує єдиний морфізм тоді і тільки тоді, коли x≤y (зрозуміло, слід відрізняти цю категорію від категорії частково впорядкованих множин).

Всі перелічені вище категорії допускають ізоморфне вкладення в категорію множин. Категорії з такою властивістю називаються конкретними. Не всяка категорія є конкретною, наприклад, категорія, об'єктами якої є всі топологічні простори, а морфізмами — класи гомотопних відображень.

Комутативні діаграми

Категорія з об'єктами X, Y, Z та морфізмами f, g

Стандартним способом опису тверджень теорії категорій є комутативні діаграми. Комутативна діаграма — це орієнтований граф, у вершинах якого знаходяться об'єкти, а стрілками є морфізми або функтори, причому результат композиції стрілок не залежить від вибраного шляху. Наприклад, аксіоми теорії категорій можна записати за допомогою діаграм:

Двоїстість

Для категорії $𝒞$ можна визначити двоїсту категорію ${𝒞}^{op}$, у якій:

• об'єкти збігаються з об'єктами початкової категорії;
• морфізми одержуються «обертанням стрілок»: ${\text{Hom}}_{{𝒞}^{op}}(B,A)\simeq {\text{Hom}}_{𝒞}(A,B)$

Взагалі, для будь-якого твердження теорії категорій можна сформулювати подвійне твердження за допомогою звернення стрілок. Часто подвійне явище позначається тим же терміном з приставкою ко- (див. приклади далі).

Справедливий принцип двоїстості: твердження р істинно в теорії категорій тоді і тільки тоді, коли в цій теорії істинно двоїсте твердження р^*. Багато понять і результатів в математиці виявилися двоїстими один одному з точки зору понять теорії категорій: ін'єктивність і сюр'єктивність, многовиди і радикали в алгебрі і т. д.

Морфізми

• Морфізм $f\in \text{Hom}(A,B)$ називається ізоморфізмом, якщо існує такий морфізм $g\in \text{Hom}(B,A)$, що $g\circ f=i{d}_A$ та $f\circ g=i{d}_B$. Два об'єкти, між якими існує ізоморфізм, називаються ізоморфними. Зокрема, тотожний морфізм є ізоморфізмом, тому будь-який об'єкт ізоморфний сам собі.

• Морфізми, в яких початок і кінець збігаються, називають ендоморфізмами. Множина ендоморфізмів $\text{End}(A)=\text{Hom}(A,A)$ є моноїдом щодо операції композиції з одиничним елементом $i{d}_A$.

• Ендоморфізми, які одночасно є ізоморфізмами, називаються автоморфізмами. Автоморфізми будь-якого об'єкта утворюють групу автоморфізмів $\text{Aut}(A)$ по композиції.

• Мономорфізм — це морфізм $f\in \text{Hom}(A,B)$ такий, що для будь-яких $g_1,g_2\in \text{Hom}(X,A)$ з $f\circ g_1=f\circ g_2$ випливає, що $g_1=g_2$.

Композиція мономорфізмів є мономорфізмом.

• Епіморфізм — це такий морфізм, що для будь-яких $g_1,g_2\in \text{Hom}(B,X)$ з $g_1\circ f=g_2\circ f$ слідує $g_1=g_2$.

• Біморфізм — це морфізм, що є одночасно мономорфізмом і епіморфізмом. Будь-який ізоморфізм є біморфізмом, зворотне, взагалі кажучи, вірно не для всіх категорій.

Мономорфізм, епіморфізм і біморфізм є узагальненнями понять ін'єктивного, сюр'єктивного і бієктивного відображення відповідно.

Універсальні об'єкти

Шаблон:Main Початковий (універсально відштовхуючий) об'єкт категорії — це такий об'єкт, з якого існує єдиний морфізм в будь-який інший об'єкт.

Якщо початкові об'єкти в категорії існують, то всі вони ізоморфні.

Двоїстим чином визначається термінальний (універсально притягуючий) об'єкт — це такий об'єкт, в який існує єдиний морфізм з будь-якого іншого об'єкта.

Приклад: У категорії Set ініціальним об'єктом є порожня множина $\mathrm{\varnothing }$, термінальним — множина з одного елементу $\{\cdot \}$.

Приклад: У категорії Group ініціальний і термінальний об'єкт збігаються — це група з одного елементу.

Добуток і сума об'єктів

• Добуток об'єктів $X_1$ та$X_2$ — це об'єкт $X_1\times X_2$ з морфізмами ${\pi }_1:X_1\times X_2\to X_1$ та ${\pi }_2:X_1\times X_2\to X_2$ такими, що для будь-якого об'єкта $Y$ з морфізмами $f_1:Y\to X_1$ та $f_2:Y\to X_2$ існує єдиний морфізм $f:Y\to X_1\times X_2$ такий, що $f\circ {\pi }_1=f_1,f\circ {\pi }_2=f_2$.

Морфізми ${\pi }_1:X_1\times X_2\to X_1$ та ${\pi }_2:X_1\times X_2\to X_2$ називаються проєкціями.

• Дуально визначається кодобуток (пряма сума): $X_1+X_2$ об'єктів $X_1$ і $X_2$. Відповідні морфізми $i_1:X_1\to X_1+X_2$ та $i_2:X_2\to X_1+X_2$ називаються вкладеннями. Не зважаючи на свою назву, в загальному випадку вони можуть і не бути мономорфізмами.

Якщо добуток і кодобуток існують, то вони визначаються однозначно з точністю до ізоморфізму.

Приклади

• У категорії Set прямий добуток A і B — це добуток в сенсі теорії множин $A\times B$, а пряма сума — диз'юнктне об'єднання $A\bigsqcup B$.
• У категорії Ring пряма сума — це тензорний добуток $A\otimes B$, а прямий добуток — сума кілець $A\oplus B$.
• У категорії Vect_K прямий добуток і пряма сума ізоморфні — це сума векторних просторів $A\oplus B$.

Фактор-категорія

Фактор-категорія — конструкція, яка є аналогічною конструкції фактор-множини або фактор-алгебри. Нехай $R$ — довільна категорія, у класі морфізмів $\mathrm{M}\mathrm{o}\mathrm{r}R$ задане відношення еквівалентності $\sim ,$ яке задовільняє наступним умовам

• якщо $\alpha \sim \beta ,$ то кінці морфізмів $\alpha$ та $\beta$ співпадають;
• якщо $\alpha \sim \beta ,\gamma \sim \delta$ та добуток $\alpha \gamma$ визначений, то $\alpha \gamma \sim \beta \delta .$

Через $[\alpha ]$ позначається клас еквівалентності морфізму $\alpha .$ Фактор-категорією категорії $ℛ$ по відношенню еквівалентності називається категорія $ℛ/\sim ,$ у якої ті самі об'єкти, що й у $ℛ,$ а для будь-якої пари об'єктів $A,B$ множина морфізмів $\mathrm{M}\mathrm{o}\mathrm{r}(A,B)\in ℛ/\sim$ складається з класів еквівалентності $[\alpha ],$ де $\alpha :A\to B$ у $R;$ добуток морфізмів $[\alpha ],[\beta ]$ визначається формулою $[\alpha ][\beta ]=[\alpha \beta ].$

Усяка мала категорія є фактор-категорії шляхів над підходячим орієнтованим графом.

Ядерна пара морфізму — узагальнення поняття еквівалентности, індукованого відображенням однієї множини у іншу. Морфізми ${\vartheta }_1,{\vartheta }_2:R\to A$ категорії $ℛ$ є ядерною парою морфізму $\alpha :A\to B,$ якщо ${\vartheta }_1\alpha ={\vartheta }_2\alpha$ та якщо для пари довільних морфізмів $\phi ,\psi :X\to A,$ для якої $\phi \alpha =\psi \alpha ,$ існує такий єдиний морфізм $\gamma :X\to R,$ що $\phi =\gamma {\vartheta }_1$ та $\psi =\gamma {\vartheta }_2.$

Функтори

Функтори — відображення категорій, що зберігають структуру. Точніше

• (Коваріантний) функтор $ℱ:𝒞\to 𝒟$ ставить у відповідність кожному об'єктові категорії $𝒞$ об'єкт категорії $𝒟$ і кожному морфізму $f:A\to B$ морфізм $F(f):F(A)\to F(B)$ так, що
  • $F(i{d}_A)=i{d}_{F(A)}$ і
  • $F(g)\circ F(f)=F(g\circ f)$.

• Контраваріантний функтор, або кофунктор — це функтор з $𝒞$ у ${𝒟}^{op}$, тобто «функтор, що перевертає стрілки».

Мала категорія

Клас об'єктів не обов'язково є множиною у сенсі аксіоматичної теорії множин. Категорія $𝒞$, у якій об'єкти $\mathrm{O}\mathrm{b}𝒞$ є множиною та морфізми $Mor(𝒞)$ є множиною, називається малою.

Нехай $ℱ:ℂ\to 𝔻$ — функтор з малої категорії у довільну. Шаром $ℱ/d$ функтора $ℱ$ над $a\in \mathrm{O}\mathrm{b}𝔻$ є категорія, об'єктами якої є пари $(a,\alpha )$ об'єктів $a\in \mathrm{O}\mathrm{b}ℂ$ та морфізмів $\alpha :Sa\to d$ категорії $𝔻$, а морфізмами $(a,\alpha )\to (b,\beta )$ між парами — трійки $(f,\alpha ,\beta )$ морфізмів $f\in ℂ(a,b),a\in 𝔻(Sa,d),\beta \in 𝔻(Sb,\beta )$ таких, що $\beta \circ Sf=\alpha .$ Двоїсто, ко-шаром $d/S$ називається категорія, яка складається з пар $(a,\alpha )$ об'єктів $a\in \mathrm{O}\mathrm{b}ℂ$ та морфізмів $\alpha :d\to Sa,$ у якій морфізмами $(a,\alpha )\to (b,\beta )$ є трійки $(f,a\to b,\alpha ,\beta ),$ які задовільняють співвідношенню $Sf\circ \alpha =\beta .$ Функтор ${\mathscr{H}}_d:d/S\to ℂ$ (або, відповідно, ${\mathscr{H}}_d:S/d\to ℂ$), який діє як $(a,\alpha )\mapsto a$ на об'єктах й як $(f,\alpha ,\beta )\mapsto f$ на морфізмах, називається забуваючим функтором.

Тензорна категорія

Нехай $𝒞$ категорія та нехай $\otimes :𝒞\times 𝒞\to 𝒞$ — функтор, які називаються тензорним добутком. Категорія називається тензорною, якщо виконуються наступні умови:

1. Заданий деякий ізоморфізм функторів $a:\otimes (\otimes \times 1)\to (1\times \otimes ).$ Це значить, що для $U,V,W,X\in 𝒞$ є ізоморфізм.
2. Виконується аксіома п'ятикутника: $\mathrm{\forall }U,V,W,X\in 𝒞a_{U,V,W\otimes X}\circ a_{U\otimes V,W,X}=(1_U\otimes a_{V,W,X})\circ a_{U,V\otimes W,X}\circ a_{U,V,W\otimes 1_X}.$
3. Є об'єкт $I,$ для якого задані натуральні ізоморфізми $l:\otimes (I\times 1)\to 1$ та $r:\otimes (1\times I)\to 1.$
4. Виконується аксіома трикутника:

$V,W\in 𝒞(1_V\otimes l_W)\circ a_{V,I,W}=r_V\otimes 1_W.$

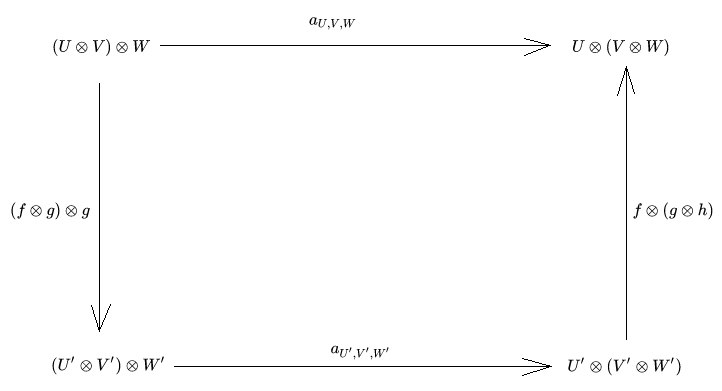
Наприклад, для трійок $U,V,W\in 𝒞$ та $f,g,h\in \mathrm{M}\mathrm{o}{\mathrm{r}}_{𝒞}$ є такий ізоморфізм $a_{U,V,W}:(U\otimes V)\otimes W\to U\otimes (V\otimes W)$, що діаграма

є комутативною.

Категорія Дрінфельда

Володимир Гершонович Дрінфельд визначив квазі-трикутну моноїдальну категорію. Нехай $ℭ$ — категорія, об'єктами якої є $𝔤$-модулі, а ${\mathrm{H}\mathrm{o}\mathrm{m}}_{ℭ}(U,W)={\mathrm{H}\mathrm{o}\mathrm{m}}_{𝔤}(U,W)[[n]].$ Це — $C$-лінійна адитивна категорія. Тепер нехай $V_1,V_2,V_3\in ℭ.$ Розгляньмо гомоморфізм $\theta :T_3[[\hslash ]]\to End(V_1\otimes V_2\otimes V_3),$ який визначається формулою $\theta (t_{ij}={\mathrm{\Omega }}_{ij})$, і ${\mathrm{\Phi }}_{V_1{V}_2{V}_3}=\theta (\mathrm{\Phi }).$ Тут $\mathrm{\Phi }$ є морфізмом асоціативності (асоціатором Дрінфельда). Через $\mathrm{\Omega }$ позначений елемент Казіміра. Через $T_3[[\hslash ]]$ позначені співвідношення шестикутника. Для довільних $V_1,V_2\in ℭ$ має місце тензорний добуток $V_1\otimes V_2.$ Морфізм асоціативності ${\mathrm{\Phi }}_{V_1{V}_2{V}_3}$ є елементом ${\mathrm{H}\mathrm{o}\mathrm{m}}_{ℭ}((V_1\otimes V_2)\otimes V_3,V_1\otimes (V_2\otimes V_3)).$ Для $V_1,V_2\in ℭ$ визначмо також скручення ${𝔖}_{V_1{V}_2}:V_1\otimes V_2\to V_2\otimes V_1$ формулою ${𝔖}_{V_1{V}_2}=s\circ \exp (\hslash \mathrm{\Omega }/2),$ де $s$ є перестановкою. Морфізми ${\mathrm{\Phi }}_{V_1{V}_2{V}_3},{𝔖}_{V_1{V}_2}$ визначають структуру квазі-трикутної категорії на $𝔖.$

Функтор Сера

Функтором Сера триангульованої $C$-лінійної $\mathrm{H}\mathrm{o}\mathrm{m}$-скінченної категорії $𝒜$ є коваріантний адитивний функтор $F:𝒜\to 𝒜,$ який комутує із зсувами, якщо має місце автоеквівалентність $F:𝒜\to 𝒜$ така, що мають місце біфункторіальні ізоморфізми

${\mathrm{H}\mathrm{o}\mathrm{m}}_{𝒜}(E,G)\cong D{\mathrm{H}\mathrm{o}\mathrm{m}}_{𝒜}(G,F(E)),$

де $D={\mathrm{H}\mathrm{o}\mathrm{m}}_C(-,k),E,G\in \mathrm{O}\mathrm{b}𝒜.$ Якщо функтор Сера існує, то він єдиний з точністю до ізоморфізму.

Для гладкого проективного многовиду $M$ розмірності $n$ й канонічного пучка ${\omega }_M={\wedge }^n{\mathrm{\Omega }}_M$ класична двоїстість Сера

$H^i(M,𝔉)\cong D{\mathrm{E}\mathrm{x}\mathrm{t}}^{n-i}(𝔉,{\omega }_M),$

де $𝔉\in \mathrm{c}\mathrm{o}\mathrm{h}(M),$ є наслідком того, що $F=-\otimes {\omega }_M[n]$ є функтором Сера на довільній категорії обмежених комплексів когерентних пучків $D^b(\mathrm{c}\mathrm{o}\mathrm{h}(M)).$ Якщо на триангульованій $C$-лінійній $\mathrm{H}\mathrm{o}\mathrm{m}$-скінченній категорії $𝒜$ є функтор Сера, то така категорія є категорією із двоїстістю Сера.

Нехай $A$ — скінченновимірна алгебра над $C,$ яка має скінченну гомологічну розмірність, $𝒜=D^b(A-\mathrm{m}\mathrm{o}\mathrm{d})$ — довільна категорія скінченновимірних лівих $A$-модулів. Наявні два функтори дуалізації, які переводять $D^b(A-\mathrm{m}\mathrm{o}\mathrm{d})$ у $D^b(\mathrm{m}\mathrm{o}\mathrm{r}-A)$ (праві моулі), й навпаки:

$D^b(A-\mathrm{m}\mathrm{o}\mathrm{d})\stackrel{\delta }{\to }{D}^b(\mathrm{m}\mathrm{o}\mathrm{d}-A)\stackrel{d}{\to }{D}^b(A-\mathrm{m}\mathrm{o}\mathrm{d}),$

$\delta (M^{*})=R{\mathrm{H}\mathrm{o}\mathrm{m}}_A(M^{*},A);d(M^{*})={\mathrm{H}\mathrm{o}\mathrm{m}}_C(M^{*},C).$

Тут $\mathrm{m}\mathrm{o}\mathrm{d}-A$ — категорія скінченнопороджених модулів над скінченновимірною $C$-алгеброю $A$ глобальної розмірності. Композиція $F=d\circ \delta$ називається функтором Накаями й є функтором Сера у категорії $𝒜=D^b(A-\mathrm{m}\mathrm{o}\mathrm{d}).$

Тріагнульована $C$-лінійна $\mathrm{H}\mathrm{o}\mathrm{m}$-скінченна категорія $𝒜$ називається категорією Калабі-Яу, якщо триангульований $n$-кратний функтор зсуву $[n]$ є функтором Сера. Найменше $n\ge 0$ називається розмірністю Калабі-Яу категорії $𝒜$ й позначається $\mathrm{C}\mathrm{Y}\mathrm{d}\mathrm{i}\mathrm{m}(𝒜).$ Якщо категорія $𝒜$ не є категорією Калабі-Яу, то $\mathrm{C}\mathrm{Y}\mathrm{d}\mathrm{i}\mathrm{m}(𝒜)=\mathrm{\infty }.$

Триангульовані категорії із двоїстістю Сера представляють інтерес тому, що на спадкових абелевих категоріях $𝔸$ Нетер є двоїстість Сера.

Мультикатегорія

Мультикатегорією є набір об'єктів $a,b,...,$ стрілок $f_1,f_2,...,$ операція композиції визначається як у звичайній категорії. У звичайній категорії область визначення $\mathrm{d}\mathrm{o}\mathrm{m}f$ — одиничний об'єкт, тоді як у мультикатегорії це скінченна множина об'єктів. Іншими словами, для звичайної категорії $a\to b,$ тоді як у мультикатегорії $\left[\begin{array}{c}{a}_1\\ a_2\\ ...\\ a_k\end{array}\right]\to b,k\in \mathbb{N}.$

Див. також

• Категорія
• Теорія груп
• Лямбда-числення
• Категорія добутку
• Теорія топосів

Література

• С. Маклейн Категории для работающего математика, — М.: ФИЗМАТЛИТ, 2004. — 352 с — ISBN 5-9221-0400-4.
• И. Букур, А. Деляну Введение в теорию категорий и функторов. — М.: Мир, 1972.
• Цаленко М. С., Шульгейфер Е. Г. Основы теории категорий. — М.: Наука, 1974.
• Adámek, Jiří; Herrlich, Horst; Strecker, George E. (1990). Abstract and concrete categories. John Wiley & Sons. ISBN 0-471-60922-6.
• Awodey, Steven (2006). Category Theory (Oxford Logic Guides 49). Oxford University Press.
• Pedicchio, Maria Cristina; Tholen, Walter (2004). Categorical foundations. Encyclopedia of Mathematics and its Applications 97. Cambridge University Press.

Посилання

• Категорій теорія Шаблон:Webarchive // Шаблон:ЕСУ
• Category Theory and Haskell Шаблон:Webarchive
• Category Theory for Programmers Шаблон:Webarchive

Шаблон:Бібліоінформація Шаблон:Розділи математики Шаблон:Інформатика Шаблон:Портали