Рівномірна неперервність

Графік $f(x)=\frac{1}{x}$ перетинає горішню і долішню риски обмежувального вікна висота × широта=$2\epsilon \times 2\delta ,$ якою маленькою не була б $\delta$, отже $f(x)$ не рівномірно неперервна. Тоді як, функція $g(x)=\sqrt{x}$ рівномірно неперервна.

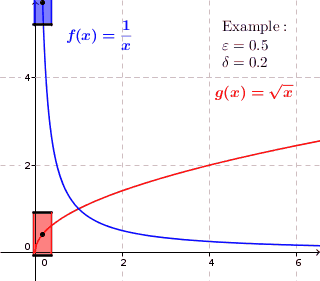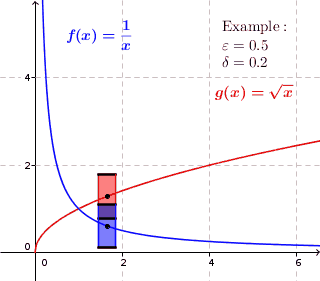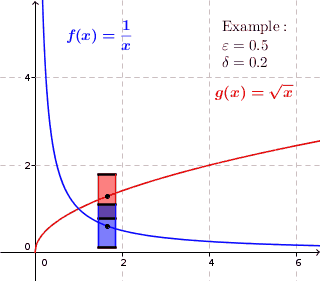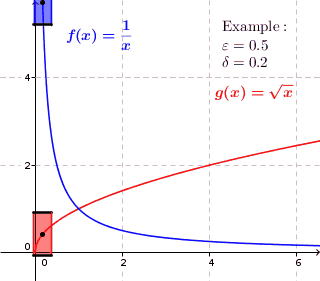
Рівномірна неперервність в математичному і функціональному аналізі — це властивість функції бути однаково неперервною в усіх точках області визначення.

Означення

Нехай дано два метричні простори $(X,{\varrho }_X)$ і $(Y,{\varrho }_Y)$. Функція $f:X\to Y$ називається рівномірно неперервною на підмножині $M\subset X,$ якщо

$\mathrm{\forall }\epsilon >0\mathrm{\exists }\delta =\delta (\epsilon )>0\mathrm{\forall }{x}_1,x_2\in M({\varrho }_X(x_1,x_2)<\delta )\Rightarrow ({\varrho }_Y(f(x_1),f(x_2))<\epsilon )$.

Зокрема, дійснозначна функція дійсного змінного $f:M\subset ℝ\to ℝ$ рівномірно неперервна, якщо

$\mathrm{\forall }\epsilon >0\mathrm{\exists }\delta =\delta (\epsilon )>0\mathrm{\forall }{x}_1,x_2\in M(|x_1-x_2|<\delta )\Rightarrow (|f(x_1)-f(x_2)|<\epsilon )$

Вибір $\delta$ у визначенні рівномірної неперервності залежить від $\epsilon$, але не від $x_1,x_2.$

Властивості

• Функція, рівномірно неперервна на множині $M,$ неперервна на ній. Зворотне, взагалі кажучи, не справджується. Наприклад, функція

$f(x)=\frac{1}{x},x\in (0,1)$

неперервна на всій області визначення, але не є рівномірно неперервною, оскільки при будь-якому $\epsilon >0$ можна вказати відрізок скільки завгодно малої довжини такий, що на його кінцях значення функції відрізнятимуться більше, ніж на $\epsilon .$ Інший приклад: функція

$f(x)=x^2,x\in (-\mathrm{\infty },+\mathrm{\infty })$

неперервна на всій числовій осі, але не є рівномірно неперервною, оскільки

$\underset{x\to \mathrm{\infty }}{\lim }(f(x+\frac{a}{x})-f(x))=\underset{x\to \mathrm{\infty }}{\lim }(x^2+2a+a^2{x}^{-2}-x^2)=2a.$

Для будь-якого $\epsilon >0$ можна вибрати відрізок як завгодно малої довжини $\epsilon /x$ такий, що різниця значень функції $f(x)=x^2$ на кінцях відрізка буде більше $\epsilon .$ Зокрема, на відрізку $(x,x+\frac{\epsilon }{x})$ різниця значень функції збігається до $2\epsilon .$

• (Теорема Кантора — Гейне) Функція, неперервна на компактній підмножині $K\subset X,$ рівномірно неперервна на ній. Зокрема якщо $f\in C([a,b]),$ то вона рівномірно неперервна на $[a,b].$
• Нехай $f:X\to Y$ це рівномірно неперервне відображення, і $\{x_n{\}}_{n=1}^{\mathrm{\infty }}$ — послідовність Коші в $X.$ Тоді $\{f(x_n){\}}_{n=1}^{\mathrm{\infty }}$ — послідовність Коші в $Y.$
• Будь-яке ліпшицеве відображення є рівномірно неперервним.

Див. також

• Рівностепенева неперервність
• Абсолютна неперервність

Джерела

• Шаблон:Фіхтенгольц.укр
• Шаблон:Бурбакі.Загальна топологія.г1-2
• Шаблон:Банах.Диференціальне та інтегральне числення