Гармонічний ряд

Шаблон:Числення В математиці, гармонічним рядом називається нескінченний розбіжний ряд:

$\sum _{k=1}^{\mathrm{\infty }}\frac{1}{k}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots .$

Обчислення

$n$-ною частковою сумою $s_n$ гармонічного ряду називається $n$-не гармонічне число:

$s_n=\sum _{k=1}^n\frac{1}{k}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots +\frac{1}{n}$

Деякі значення часткових сум

$\begin{array}{ccc}{s}_1& =& 1\\ \\ s_2& =& \frac{3}{2}& =& 1,5\\ \\ s_3& =& \frac{11}{6}& \approx & 1,833\\ \\ s_4& =& \frac{25}{12}& \approx & 2,083\end{array}$

$\begin{array}{ccccc}{s}_5& =& \frac{137}{60}& \approx & 2,283\\ \\ s_6& =& \frac{49}{20}& =& 2,45\\ \\ s_7& =& \frac{363}{140}& \approx & 2,593\\ \\ s_8& =& \frac{761}{280}& \approx & 2,718\end{array}$

Розбіжність ряду

Гармонічний ряд розбіжний, щоправда розбіжність є дуже повільною (для того, щоб часткова сума перевищила 100, необхідно близько 10⁴³ елементів ряду).

Доведення 1

Розбіжність ряду можна довести погрупувавши доданки так:

$\begin{array}{cc}\sum _{k=1}^{\mathrm{\infty }}\frac{1}{k}& =1+\left[\frac{1}{2}\right]+[\frac{1}{3}+\frac{1}{4}]+[\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}]+[\frac{1}{9}+\cdots ]+\cdots \\ & >1+\left[\frac{1}{2}\right]+[\frac{1}{4}+\frac{1}{4}]+[\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}]+[\frac{1}{16}+\cdots ]+\cdots \\ & =1+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\cdots .\end{array}$

Останній ряд, очевидно, розбіжний, що доводить твердження.

Доведення 2

Припустимо, що гармонічний ряд збіжний і його сума рівна $S$:

$\sum _{k=1}^{\mathrm{\infty }}\frac{1}{k}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots =S$

Тоді перегрупувавши доданки одержимо:

$S=(1+\frac{1}{3}+\frac{1}{5}+\frac{1}{7}+\cdots )+(\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+\cdots )$

Винесемо із других дужок $\frac{1}{2}$:

$S=(1+\frac{1}{3}+\frac{1}{5}+\frac{1}{7}+\cdots )+\frac{1}{2}(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots )$

Замінимо вираз в других дужках на $S$:

$S=(1+\frac{1}{3}+\frac{1}{5}+\frac{1}{7}+\cdots )+\frac{1}{2}S$

Перенесемо $\frac{1}{2}S$ в ліву частину:

$\frac{1}{2}S=(1+\frac{1}{3}+\frac{1}{5}+\frac{1}{7}+\cdots )$

Замінивши $S$ сумою ряду одержимо:

$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+\cdots =1+\frac{1}{3}+\frac{1}{5}+\frac{1}{7}+\cdots$

Ця рівність хибна, оскільки одиниця більша однієї другої, одна третя більше однієї четвертої, і так далі. Таким чином припущення про збіжність ряду привело до суперечності.

Доведення 3

На початок запишемо суму геометричної прогресії:

$\frac{1}{1-x}=1+x+x^2+x^3+x^4+...$

де |x|<1.

Візьмемо інтеграл з обох сторін, внаслідок чого одержимо:

$-\ln (1-x)=x+\frac{x^2}{2}+\frac{x^3}{3}+...$

Перейшовши до границі при $x\to 1$ одержуємо рівність:

$-\underset{x\to 1}{\lim }\ln (1-x)=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...=\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n}$.

Оскільки $-\underset{x\to 1}{\lim }\ln (1-x)=-(-\mathrm{\infty })=\mathrm{\infty }$, то також має місце $\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n}=\mathrm{\infty }$

Тобто гармонічний ряд є розбіжним.

Пов'язані ряди

Знакопереміжний гармонічний ряд

Перші 14 часткових сум знакопереміжного гармонійного ряду (чорні відрізки) збігаються до натурального логарифму 2 (червона пряма).

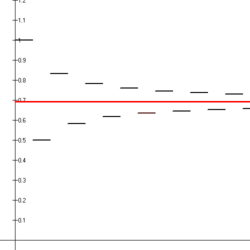
Ряд $$\sum _{n=1}^{\mathrm{\infty }}\frac{(-1{)}^{n+1}}{n}=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\cdots$$ називається знакопереміжним гармонічним рядом. Він умовно збіжний за теоремою Лейбніца, але не абсолютно збіжний. Його сума - Шаблон:Iw.Шаблон:R

Використання знаків що чергуються з лише непарними знаменниками дасть пов'язаний ряд Лейбніца для знаходження Шаблон:PiШаблон:R $$\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n}{2n+1}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots =\frac{\pi }{4}.$$

Див. також

• Гармонічне число
• Константа Майсселя — Мертенса

Література

• Шаблон:Фіхтенгольц.укр
• Шаблон:Клепко ВМ
• Шаблон:Дороговцев.Математичний аналіз.ч1
• Шаблон:Банах.Диференціальне та інтегральне числення