Метеликова діаграма

Шаблон:Нп, що з'єднує входи $x$ (ліворуч) із залежними від них виходами $y$ (праворуч) для кроку у «метелику» за алгоритмом Кулі–Т'юкі за основою 2 для швидкого перетворення Фур'є. Ця діаграма нагадує метелика (як у метелика морфо, показаного для порівняння), звідси й назва, хоча в деяких країнах її також називають діаграмою пісочного годинника.

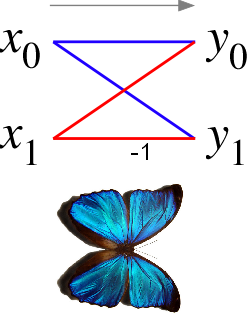
У контексті алгоритмів швидкого перетворення Фур'є «метелик» — це елемент обчислення, що об'єднує результати менших дискретних перетворень Фур'є (ДПФ) для створення більших ДПФ або, навпаки, розкладає більші ДПФ на менші. Назва «метелик» походить від форми діаграми потоку даних для другого степеня, як описано нижче. Вважається, що цей термін вперше опубліковано у технічному звіті MIT за 1969 рік. Подібна структура зустрічається й у алгоритмі Вітербі, який використовується для пошуку найбільш імовірної послідовності прихованих станів.

Термін «метелик» найчастіше використовується у контексті алгоритму ШПФ Кулі–Тьюкі, який рекурсивно розбиває ДПФ розмірності $n=rm$ на $r$ менших перетворень розмірності $m$, де $r$ є «основою» перетворення. Ці менші ДПФ потім об'єднуються за допомогою метеликів розмірності $r$, що фактично є ДПФ розмірності $r$ (і так $m$ разів на відповідних виходах підперетворень), попередньо помножених на корені з одиниці (відомі як Шаблон:Нп). Це описує процес «децимації в часі». Можна також виконати кроки у зворотному порядку, що відоме як «децимація в частоті», де метелики застосовуються спочатку, а потім множаться на обертальні коефіцієнти. Додаткову інформацію можна знайти у статті про Кулі–Тьюкі ШПФ.

Метеликова діаграма за основою 2

У випадку алгоритму Кулі–Тьюкі за основою 2 метелик є просто ДПФ основи 2, який приймає два входи $(x_0,x_1)$ — виходи двох підперетворень — і перетворює їх на два вихідні значення $(y_0,y_1)$ за формулою (без урахування Шаблон:Нп):

$y_0=x_0+x_1,$

$y_1=x_0-x_1.$

Якщо зобразити діаграму потоку даних для цієї пари операцій, що перетворюють ($x_0$, $x_1$) на ($y$, $y_1$), лінії будуть перетинатися і нагадуватимуть крила метелика. Звідси і походить назва (див. також ілюстрацію праворуч).

ШПФ за основою 2 із децимацією в часі розбиває ДПФ довжини $N$ на два ДПФ довжини $N/2$, за якими йде крок об'єднання, що складається з багатьох операцій «метелика».

Щобільше, алгоритм БПФ з проріджуванням у часі з основою 2 на $n=2p$ вхідних даних, що використовує первинний корінь $n$-го ступеня з одиниці ${\omega }_n^k=e^{-\frac{2\pi ik}{n}}$ залежить від $O$ ($n{\log }_{2}n$) метеликів виду:

$y_0=x_0+x_1{\omega }_n^k,$

$y_1=x_0-x_1{\omega }_n^k,$

де $k$ — ціле число, що залежить від частини перетворення, яка обчислюється. Водночас відповідне зворотне перетворення можна математично виконати, замінивши $\omega$ на ${\omega }^{-1}$ (і, можливо, помноживши на загальний масштабний коефіцієнт, залежно від умов нормалізації). Також можна безпосередньо інвертувати метеликів:

$x_0=\frac{1}{2}(y_0+y_1),$

$x_1=\frac{{\omega }_n^{-k}}{2}(y_0-y_1),$

що відповідає алгоритму ШПФ з децимацією по частоті.

Інші застосування

Метелик також застосовується для покращення випадковості великих масивів частково випадкових чисел, встановлюючи причинно-наслідковий зв'язок між кожним 32- або 64-бітним словом і всіма іншими словами за допомогою вибраного алгоритму хешування. Це гарантує, що зміна будь-якого біта призводить до зміни всіх бітів у великому масиві.

Див. також

• Шаблон:Нп
• Шаблон:Нп
• Шаблон:Нп

Посилання

• Пояснення ШПФ і діаграм метеликів .
• Діаграми метеликів різних реалізацій ШПФ (Radix-2, Radix-4, Split-Radix) .