Конформно-евклідова модель

Замощення гіперболічної площини правильними трикутниками.

Конфо́рмно-евклі́дова моде́ль або моде́ль Пуанкаре́ — модель гіперболічного простору. Існують різновиди моделі — в колі (стереографічна проєкція) і на півплощині для гіперболічної планіметрії, а також у кулі і в півпросторі — для гіперболічної стереометрії, відповідно.

Конформно-евклідова модель має таку назву тому, що гіперболічні кути дорівнюють відповідним кутам на евклідовій площині між відповідними півдотичними. Для проєктивної моделі, гіперболічні кути дорівнюють евклідовим кутам лише у виключних випадках, наприклад, така рівність є у початку координат проєктивної моделі.

Історія

Цю модель, як і проективну модель і модель псевдосфери, запропонував Еудженіо Бельтрамі. Метрику в конформно-евклідовій моделі використано також у знаменитій лекції Рімана «Про гіпотези, що лежать в основі геометрії», але зв'язок з гіперболічною геометрією виявив саме Бельтрамі. Згодом Анрі Пуанкаре виявив зв'язки цієї моделі з задачами теорії функцій комплексної змінної, що дало одне з перших серйозних застосувань гіперболічної геометрії.

Моделі у крузі і в кулі

Конформно-евклідова модель у крузі.

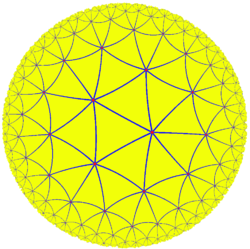
За гіперболічну площину приймається внутрішність круга (див. мал.) в евклідовому просторі; межа даного круга (коло) називається «абсолютом». Роль геодезичних ліній виконують дуги кіл $(a,b,b^{\prime })$, перпендикулярних до абсолюту, і його діаметри; роль рухів — перетворення, одержувані комбінаціями інверсій відносно кіл, дуги яких служать прямими.

Метрика $ds$ гіперболічної площини в конформно-евклідовій моделі в одиничному крузі є:

$d{s}^2=\frac{4}{(1-(x^2+y^2){)}^2}(d{x}^2+d{y}^2),$

де $x$ і $y$ — вісь абсцис і ординат, відповідно.

Аналогічно, для конформно-евклідової моделі в кулі роль абсолюту виконує обмежувальна сфера в тривимірному евклідовому просторі, а гіперболічним простором є внутрішність кулі.

Відстані

У комплексних координатах на одиничному колі відстані можна обчислити за допомогою такої формули:

$\mathrm{t}\mathrm{h}[\frac{1}{2}\cdot d_h(z,w)]=\left|\frac{z-w}{1-z\cdot \overline{w}}\right|.$

Відстань можна виразити через подвійне відношення. Якщо на дузі $w_1$, $z_1$ точки розташовано в такому порядку: $w_1$, $w$, $z$, $z_1$ то відстань між точками $w$ і $z$, у гіперболічній геометрії дорівнює

$d_h(z,w)=\ln (\frac{z-w_1}{z-z_1}:\frac{w-w_1}{w-z_1})$.

Моделі на півплощині й у півпросторі

В моделі Пуанкаре в півплощині за гіперболічну площину приймається верхня півплощина. Пряма, що обмежує півплощину (тобто вісь абсцис), називається «абсолютом». Роль прямих виконують півкола з центрами на абсолюті, що містяться в цій півплощині, і перпендикулярні до абсолюту промені, що починаються на ньому (тобто вертикальні промені). Роль рухів — перетворення, одержувані композицією скінченного числа інверсій із центром на абсолюті і осьових симетрій, осі яких перпендикулярні до абсолюту.

Метрика $ds$ гіперболічної площини у конформно-евклідовій моделі у верхній півплощині має вигляд: $d{s}^2=\frac{1}{v^2}(d{u}^2+d{v}^2)$, де $u$ і $v$ — прямокутні координати, відповідно паралельно і перпендикулярно до абсолюту.

Відповідно, в конформно-евклідовій моделі в півпросторі роль абсолюту виконує площина в тривимірному евклідовому просторі, а гіперболічним простором є півпростір, що лежить на цій площині.

Див. також

• Теорема Піка — інваріантна форма леми Шварца, що використовує відстані в конформно-евклідовій моделі.
• Ідеальний трикутник

Література

• Черников Н. А. Преобразование Боголюбова и планиметрия Лобачевского. Раздел 4, сравнение двух моделей Пуанкаре. Шаблон:Недоступная ссылка
• Самаров К., Уроев В. «Модель Пуанкаре». — Журнал «Квант». — 1984 год. — номер 6. Шаблон:Webarchive