Розшарований добуток

Розшарований добуток (також декартів квадрат) — теоретико-категорне поняття, яке можна задати як границю діаграми, що складається з двох морфізмів: $X\to Z\leftarrow Y.$ Розшарований добуток позначається $X{\times }_{Z}Y.$

Двоїстим поняттям є розшарований кодобуток.

Універсальна властивість

Нехай в категорії $C$ дана пара морфізмів $f:X\to Z$ і $g:Y\to Z.$

Розшарованим добутком $X$ і $Y$ над $Z$ називається об'єкт $P=X{\times }_{Z}Y$ разом з морфізмами $p_1,p_2,$ для яких діаграма нижче є комутативною:

Окрім того, розшарований добуток має бути універсальним об'єктом з такою властивістю: для будь-якого об'єкта $Q,$ з парою морфізмів $q_1:Q\to X,q_2:Q\to Y,$ які разом із $(f,g)$ утворюють комутативний квадрат, існує єдиний морфізм $u:Q\to P,$ такий що наведена нижче діаграма є комутативною:

Внутрішній квадрат цієї діаграми, утворений морфізмами $f,g,p_1,p_2$ називається також декартовим (або коуніверсальним) квадратом для пари морфізмів $f$ і $g.$

Як і інші об'єкти, задані за допомогою універсальних властивостей, розшарований добуток не обов'язково існує, але якщо існує, то є визначеним з точністю до ізоморфізму.

Приклади

• В категорії множин розшарованим добутком множин $X$ і $Y$ з відображеннями $f:X\to Z$ і $g:Y\to Z$ називається множина

$X{\times }_{Z}Y=\{(x,y)\in X\times Y|f(x)=g(y)\}$

разом з природними проєкціями на компоненти.

Також Розшарований добуток у $𝐒𝐞𝐭$ можна описувати двома асиметричними способами:

$X{\times }_{Z}Y$

$\cong \coprod _{x\in X}{g}^{-1}[\{f(x)\}]$

$\cong \coprod _{y\in Y}{f}^{-1}[\{g(y)\}],$

• Аналогічним чином визначається розшарований добуток в категорії комутативних кілець з тою лише специфікою, що всі відображення у цьому випадку є гомоморфізмами кілець.

• Прообраз підмножини теж можна інтерпретувати як розшарований добуток. Нехай є деяке відображення Шаблон:Math і підмножина Шаблон:Math. Нехай Шаблон:Mvar позначає відображення включення Шаблон:Math. Тоді розшароване відображення Шаблон:Mvar і Шаблон:Mvar (у категорії Шаблон:Math) можна інтерпретувати, як прообраз Шаблон:Math разом із його включенням у Шаблон:Mvar

Шаблон:Math

і обмеженням відображення Шаблон:Mvar на Шаблон:Math

Шаблон:Math.

• Якщо A і B є підмножинами множини C, то розшарованим добутком відображень включення є перетин множин із відповідними відображеннями включення у A і B.

Властивості

• У категорії із термінальним об'єктом Шаблон:Mvar, розшарований добуток Шаблон:Math є звичайним добутком Шаблон:Math.
• Якщо Шаблон:Mvar у наведених в означенні діаграмах є мономорфізмом то Шаблон:Math теж є мономорфізмом. Також якщо Шаблон:Mvar є мономорфізмом, то мономорфізмом є також і Шаблон:Math.
• Попереднє твердження є також справедливим і для ізоморфізмів, зокрема Шаблон:Math для будь-якого морфізму Шаблон:Math (де Шаблон:Math є одиничним морфізмом).
• У абелевих категоріях розшарований добуток завжди існує і має властивість збереження ядра, а саме: якщо

є відповідною комутативною діаграмою і Шаблон:Math є ізоморфізмом, то ізоморфізмом є Шаблон:Math. Звідси можна отримати комутативну діаграму, де всі рядки і стовпці є точними:

$\begin{array}{ccccccc}& & & & 0& & 0\\ & & & & \downarrow & & \downarrow \\ & & & & L& =& L\\ & & & & \downarrow & & \downarrow \\ 0& \to & K& \to & P& \to & Y\\ & & \parallel & & \downarrow & & \downarrow \\ 0& \to & K& \to & X& \to & Z\end{array}$

• Існує натуральний ізоморфізм (A×_CB)×_B D ≅ A×_CD. У явному вигляді:
  • якщо задано морфізми f : A → C, g : B → C і h : D → B і
  • розшарований добуток f і g є заданий морфізмами r : P → A і s : P → B, і
  • розшарований добуток s і h є заданий морфізмами t : Q → P і u : Q → D ,
  • тоді розшарований добуток f і gh є заданий морфізмами rt : Q → A і u : Q → D.

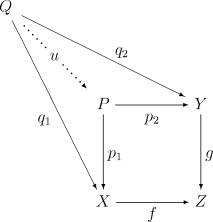
Графічно це можна подати так: з двох комутативних діаграм розшарованих добутків, що розташовані поруч і мають спільний морфізм, утворюється комутативна діаграма розшарованого добутку, якщо ігнорувати спільний морфізм. Приклад цього на комутативній діаграмі:

$\begin{array}{ccccc}Q& \stackrel{t}{\to }& P& \stackrel{r}{\to }& A\\ {\downarrow }_u& & {\downarrow }_s& & {\downarrow }_f\\ D& \stackrel{h}{\to }& B& \stackrel{g}{\to }& C\end{array}$

Див. також

• Добуток (теорія категорій)

Література

• Adámek, Jiří, Herrlich, Horst, & Strecker, George E.; (1990). Abstract and Concrete Categories Шаблон:Webarchive (4.2MB PDF). John Wiley & Sons. Шаблон:Isbn.
• Шаблон:Cite book