Чудові точки трикутника

Чудові точки трикутника — точки, розташування яких однозначно визначається трикутником і не залежить від того, в якому порядку беруться сторони і вершини трикутника.

Зазвичай вони розташовані всередині трикутника, але це не обов'язково. Зокрема, точка перетину висот може лежати поза трикутником.

Енциклопедія чудових точок трикутника (Шаблон:Lang-en) містить понад 32 тис. (станом на 2019) «центрів трикутника» — точок, пов'язаних з геометрією трикутника.

Деякі приклади чудових точок трикутника

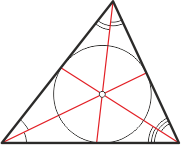
Точки перетину:

• медіан — центроїд, центр ваги (мас);
• бісектрис — інцентр або центр вписаного кола;
• висот — ортоцентр;
• серединних перпендикулярів — центр описаного кола;

Центроїд	Інцентр	Ортоцентр	Центр описаного кола

Якщо хоча б дві з цих чотирьох чудових точок трикутника збігаються, то трикутник є правильним.

Точки перетину:

Центр зовнівписаного кола

• бісектрис зовнішніх кутів — центр зовнівписаного кола;
• антибісектрис — центр антибісектрис;
• симедіан — точка Лемуана;
• бісектрис серединного трикутника (його інцентра) — центр Шпікера;
• кліверів трикутника — також центр Шпікера;
• трьох (або навіть двох) кіл, побудованих, як на діаметрі, на відрізку, що з'єднує основи внутрішньої і зовнішньої бісектриси, випущених з одного кута, — дві точки Аполлонія;

Точки перетину відрізків, що з'єднують вершини трикутника:

• з точками дотику протилежних сторін і вписаного кола — точка Жергонна;
• з точками дотику протилежних сторін і зовнівписаних кіл — точка Наґеля;

Точка Жергонна

Точка Нагеля

• з відповідними вільними вершинами рівносторонніх трикутників, побудованих на сторонах трикутника (назовні) — перша точка Торрічеллі;
• з відповідними вільними вершинами правильних трикутників, побудованих всередину трикутника — друга точка Торрічеллі;
• з відповідними вільними вершинами трикутників, подібних до початкового трикутника і побудованих на його сторонах — точки Брокара.

Мінімаксні точки трикутника

Мінімаксними (екстремальними) точками трикутника називаються точки, в яких досягається мінімум деякої функції, наприклад, суми степенів відстаней до сторін або вершин трикутника.

Мінімаксними точками трикутника є:

• точка перетину трьох медіан, що має найменшу суму квадратів відстаней до вершин трикутника (теорема Ляйбніца);
• точка перетину трьох медіан трикутника, єдина точка трикутника така, що проведені через неї три чевіани ділять своїми кінцями сторони трикутника на шість відрізків. При цьому добуток довжин трьох з цих шести відрізків, які не мають спільних кінців, максимальний;
• перша точка Торрічеллі, що має найменшу суму відстаней до вершин трикутника з кутами не більше 120 градусів;
• точка Лемуана, що має найменшу суму квадратів відстаней до сторін трикутника;
• основи висот гострокутного трикутника утворюють ортотрикутник, який має найменший периметр з усіх трикутників, вписаних у даний трикутник.

Ізо-точки трикутника

Ізо-точками є точки трикутника, що дають будь-які рівні параметри трьох трикутників, які утворюються при з'єднанні ізо-точки відрізками з трьома вершинами трикутника. В результаті утворюється фігура типу «око дракона» (див. рис.)

Око дракона

Ізо-точки трикутника, що утворюють фігуру типу «око дракона»:

• ортоцентр (дає три трикутники з трьома рівними радіусами трьох описаних навколо них кіл),
• точка перетину медіан (дає три трикутники з трьома рівними площами)
• інцентр (дає три трикутники з трьома рівними висотами)
• центр описаного кола (дає три рівнобедрених трикутники з трьома рівними парами сторін),
• точка рівних периметрів $P$ або ізопериметрична точка (дає три трикутники з трьома рівними периметрами),
• точка Торрічеллі (перша) (дає три трикутники з трьома рівними тупими кутами в $120^{\circ }$).
• Точка розбиття трикутника на три трикутники з трьома однаковими радіусами вписаних кіл
• Центр Шпікера трикутника є радикальним центром трьох його зовнівписаних кіл (має три пари рівних дотичних відразу до трьох зовнівписаних кіл).

Ізо-точки трикутника, що утворюють фігуру типу «Трилистник (вузол)»:

• Центр Шпікера $S$ є точкою перетинів прямих $AX$, $BY$ і $CZ$, де $XBC$, $YCA$ і $ZAB$ подібні, рівнобедрені та однаково розташовані, побудовані на сторонах трикутника $ABC$ зовні, що мають один і той самий кут біля основи $\mathrm{arctg}[\mathrm{tg}(A/2)\mathrm{tg}(B/2)\mathrm{tg}(C/2)]$.
• Перша точка Наполеона $N_1$, як і центр Шпікера, є точкою перетинів прямих $AX$, $BY$ і $CZ$, де $XBC$, $YCA$ і $ZAB$ подібні, рівнобедрені та однаково розташовані, побудовані на сторонах трикутника $ABC$ зовні, що мають один і той самий кут біля основи $30^{\circ }.$
• Тут треба було б перерахувати всі точки, що лежать на гіперболі Кіперта.

Із-точки трикутника, що утворюють фігуру типу «Квітка традесканції» наступні:

• точка перетину медіан утворює трьома малими відрізками чевіан три чотирикутники з рівними площами;
• точка перетину бісектрис утворює трьома перпендикулярами до трьох сторін трикутника три чотирикутники — дельтоїди з двома однаковими у всіх суміжними сторонами. Інша пара рівних суміжних сторін у загальному випадку у всіх різна. У всіх трьох дельтоїдів є пара рівних протилежних кутів $90^{\circ }$. Вони — вписано-описані чотирикутники.
• Три кола, проведені всередині трикутника через точку Мікеля, перетинають сторони трикутника в трьох точках. Три хорди, проведені через точку Мікеля, і три точки перетину трьох кіл з трьома різними сторонами трикутника, утворюють рівні кути зі сторонами.

Література

• Бевз Г. П. Геометрія трикутника. Навчально-методичний посібник для загальноосвітніх навчальних закладів. — К.:Генеза, 2005. — 120 с.: іл.
• Зетель С. И. Новая геометрия треугольника. Пособие для учителей. 2-е издание. М.: Учпедгиз, 1962.
• Енциклопедія для дітей. Т. 11. Математика/Голов. ред. М. Д. Аксьонова. — М: Аванта +, 2001. — 688 c.: іл.
• Шаблон:Книга
• Шаблон:Стаття

Посилання

• Енциклопедія центрів трикутника Шаблон:WebarchiveШаблон:Ref-en
• Енциклопедія центрів трикутника