Поверхня Каталана
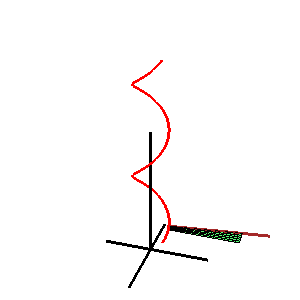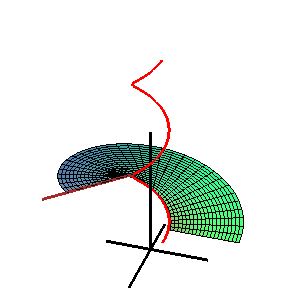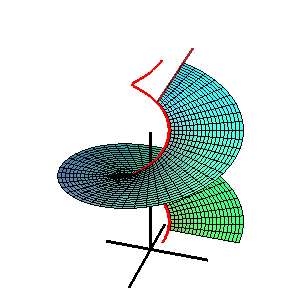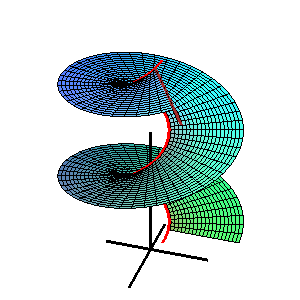
Шаблон:Не плутати Поверхня Каталана — лінійчата поверхня, для якої всі твірні паралельні фіксованій площині.
Названа на честь бельгійського математика Шаблон:Нп.
Векторне рівняння поверхні Каталана задається формулою
- r = s(u) + v L(u), де r = s(u) крива в просторі та L(u) є орт, що задає твірну пряму u = u. Всі вектори L(u) паралельні одній площині, яка описується наступною умовою: мішаний добуток [L(u), L' (u), L" (u)] = 0.
Параметричне рівняння поверхні Каталана:
Якщо всі твірні поверхні Каталана перетинають фіксовану пряму, то поверхня називається коноїдом.
Каталан довів, що гелікоїд та площина є єдиними лінійчатими мінімальними поверхнями.