Логарифмічна спіраль

Побудова логарифмічної спіралі. Анімація.

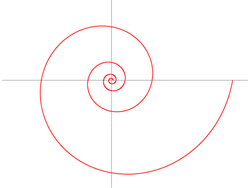
Логарифмічна спіраль або ізогональна спіраль — особливий вид спіралі, що часто зустрічається в природі. Логарифмічна спіраль була вперше описана Декартом і пізніше інтенсивно досліджена Бернуллі, який називав її Spira mirabilis — «дивовижна спіраль». Власне термін «логарифмічна спіраль» (Шаблон:Lang-fr) першим вжив П'єр Варіньон^[1].

Рівняння

У полярних координатах рівняння кривої може бути записано як

r = a e^{b θ}

або

ϑ = \frac{1}{b} \ln (r / a),

що пояснює назву «логарифмічна».

У параметричній формі його може бути записано як

x (t) = r \cos t = a e^{b t} \cos t,

y (t) = r \sin t = a e^{b t} \sin t,

де a, b- дійсні числа.

Властивості

Кут, що утворюється дотичною в довільній точці логарифмічної спіралі з радіус-вектором точки дотику, постійний і залежить лише від параметра b.
- У термінах диференціальної геометрії це може бути записано як
  $\frac{⟨ 𝐫 (θ), 𝐫^{'} (θ) ⟩}{‖ 𝐫 (θ) ‖ ‖ 𝐫^{'} (θ) ‖} = \frac{b}{\sqrt{1 + b^{2}}} = \cos φ .$
Похідна функції $𝐫^{'} (ϑ)$ пропорційна параметру b. Іншими словами, він визначає, наскільки щільно і в якому напрямку закручується спіраль. У граничному випадку, коли $b = 0 (φ = π / 2)$ спіраль вироджується в коло радіусу a. Навпаки, коли b прямує до нескінченності $(φ \to 0),$ спіраль наближається до прямої лінії. Кут, що доповнює $φ$ до 90 °, називають нахилом спіралі.
Розмір витків логарифмічної спіралі поступово збільшується, але їх форма залишається незмінною. Можливо, внаслідок цієї властивості, логарифмічна спіраль з'являється в багатьох зростаючих формах, подібних до мушель молюсків і квіток соняшників.

Цікаві факти

Якоб Бернуллі бажав, щоб на його могилі було викарбувано логарифмічну спіраль, але на його надгробку помилково зобразили спіраль Архімеда. Проте напис, вигравіюваний навколо спіралі згідно з заповітом (Шаблон:Lang-la — «змінена, я знов воскресаю»), свідчить, що йдеться саме про логарифмічну спіраль, яка має властивість зберігати свою форму після різноманітних перетворень.