Полілогарифм
Перейти до навігації
Перейти до пошуку
Полілогарифм — спеціальна функція, що позначається і визначається як нескінченний степеневий ряд
де s і z — комплексні числа, причому
. Для інших z робиться узагальнення за допомогою аналітичного продовження.
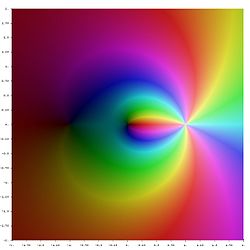
- Карта висот полілогарифма на комплексній площині
Частковим випадком є
, за якого
. Функції
і
отримали назви дилогарифма і трилогарифма відповідно. Для полілогарифмів різних порядків виконується співвідношення
Альтернативними визначеннями полілогарифма є інтеграли Фермі — Дірака і Бозе — Ейнштейна.
Окремі значення
Див. також
Література
- Шаблон:Книга-ру (this 1826 manuscript was only published posthumously.)
- Шаблон:Книга-ру
- Шаблон:Статья
- Шаблон:Cite arxiv
- Шаблон:Книга-ру
- Шаблон:Статья
- Шаблон:Статья
- Шаблон:Статья
- Шаблон:Статья
- Шаблон:Статья
- Шаблон:Статья
- Шаблон:Статья
- Шаблон:Книга-ру
- Шаблон:Статья
- Шаблон:Cite web
- Шаблон:Книга-ру
- Шаблон:Статья
- Шаблон:Cite arxiv
- Шаблон:Книга-ру
- Шаблон:Статья
- Шаблон:Статья
- Шаблон:Статья
- Шаблон:Книга-ру
- Шаблон:Книга-ру
- Шаблон:Книга-ру
- Шаблон:Статья
- Шаблон:Статья
- Шаблон:Статья
- Шаблон:Статья
- Шаблон:Книга-ру (see § 1.2, «The generalized zeta function, Bernoulli polynomials, Euler polynomials, and polylogarithms», p. 23.)
- Шаблон:Статья
- Шаблон:Статья
- Шаблон:Книга-ру
- Шаблон:Статья
- Шаблон:Cite arxiv
- Шаблон:Книга-ру
- Шаблон:Cite web
- Шаблон:Cite conference (also appeared as «The remarkable dilogarithm» in Journal of Mathematical and Physical Sciences 22 (1988), pp. 131—145, and as Chapter I of Шаблон:Harv.)
- Шаблон:Книга-ру