Модель Ремзі — Касса — Купманса

Френк Пламптон Ремзі

Тьялінг Чарльз Купманс

Модель Ремзі — Касса — Купманса (модель Ремзі, неокласична модель економічного зростання, Шаблон:Lang-en) — неокласична модель екзогенного економічного зростання в умовах досконалої конкуренції. Зробила внесок у розуміння того, яким чином рішення індивідів формують норму заощаджень в економіці. Оптимальна динаміка споживання з моделі (правило Кейнса — Ремзі) виявилася вдалою заміною екзогенної норми заощаджень і потім застосовувалася і в пізніших моделях економічного зростання. Разом з тим модель не дає задовільного пояснення міжкраїнним відмінностям у рівні доходу на душу населення. Розроблена одночасно і незалежно один від одного Тьялінгом Купмансом і Девідом Кассом з використанням ідей Френка Ремзі 1963 року.

На ілюстрації також показано динаміку норми заощаджень із наближенням до рівноважного стану.

Історія створення

У перших моделях економічного зростання (модель Солоу, модель Харрода — Домара) використовувалися екзогенно задавані параметри: «норма заощаджень» і «темп науково-технічного прогресу», від яких, зрештою, і залежать темпи зростання економіки. Дослідники ж хотіли отримати обґрунтування темпів економічного зростання внутрішніми (ендогенними) факторами, оскільки моделі з нормою заощаджень мали низку недоліків. Ці моделі не пояснювали стійких відмінностей рівнів і темпів зростання між країнами, що розвиваються, і розвиненими країнами. Для пояснення норми заощаджень як наслідків рішень економічних агентів, дослідники звернулися до праці Френка Ремзі «Математична теорія заощаджень»Шаблон:Sfn, опублікованій в Шаблон:Iw ще в грудні 1928 року. У ній виведено міжчасову функцію корисності споживача і знайдено умову оптимального вибору споживача. Використовуючи ідеї Френка Ремзі, майбутній лауреат Нобелівської премії з економіки Тьялінг Купманс у праці «Оптимальне зростання в агрегованій моделі накопичення капіталу», опублікованій як «праця для обговорення» в Єльському університеті 6 грудня 1963 року Шаблон:Sfn, і виданій у докладнішому варіанті в збірнику The Econometric Approach to Development Planning 1965 рокуШаблон:Sfn, і Девід Касс у праці «Оптимальне зростання в агрегованій моделі накопичення капіталу», виданій у липні 1965 року в журналі Шаблон:IwШаблон:Sfn представили модель Ремзі — Касса — КупмансаШаблон:SfnШаблон:SfnШаблон:SfnШаблон:Sfn (також відому як модель РемзіШаблон:SfnШаблон:SfnШаблон:Sfn, неокласична модель економічного зростанняШаблон:Sfn), головною особливістю якої стало визначення норми заощаджень у ході розв'язування задач оптимізації споживачами та фірмами, що взаємодіють в умовах досконалої конкуренціїШаблон:SfnШаблон:Sfn.

Роботи Девіда Касса і Тьялінга Купманса фактично викладають однакову модель (крім умови трансверсальності, яку запровадив Касс). Хоча працю Касса опубліковано пізніше і в ній є посилання на роботу КупмансаШаблон:Sfn, при цьому Купманс, у свою чергу, у виданій повній версії роботи, в якій також з'являється умова трансверсальності, посилається на дисертацію КассаШаблон:Sfn. Обидва дослідники припускали, що дійшли цієї моделі «одночасно і незалежно один від одного». Докладно історію з назвою даної моделі викладено в роботі Стівена Спіра та Воррена Янга «Оптимальні заощадження та оптимальне зростання: модель Ремзі — Малінво — Купманса»Шаблон:Sfn. У ній автори відзначають внесок Едмона Малінво, який сформулював умову трансверсальності раніше від Касса, проте не застосував її до розглянутої моделі.

Опис моделі

Базові передумови моделі

У моделі розглядається закрита економіка. Фірми максимізують свій прибуток, а споживачі — корисність. Фірми діють за умов досконалої конкуренції. Виготовляється лише один продукт $Y$, який використовується як для споживання $C$, так і для інвестицій $I$. Темпи технологічного прогресу $g$, зростання населення $n$ та норма вибуття капіталу $\delta$ — сталі й задаються екзогенно. Працівником і споживачем у моделі виступає індивід, що живе нескінченно (або домогосподарство). Передбачається, що між різними поколіннями існують альтруїстичні зв'язки, приймаючи рішення, домогосподарство враховує ресурси і потреби не тільки нинішніх, але й майбутніх своїх членів, що робить його рішення аналогічними рішенням індивіда, який живе нескінченно. Час $t$ змінюється неперервноШаблон:SfnШаблон:SfnШаблон:SfnШаблон:Sfn.

Доходи індивіда складаються із заробітної плати $w_t$ та надходжень від активів $r{a}_t$. Активи індивіда $a_t$ можуть бути як додатними, так і від'ємними (борг). Відсоткову ставку $r_t$ за доходами з активів та за боргом у моделі прийнято однаковою. У зв'язку з цим у моделі є умова відсутності схеми Понці (фінансової піраміди): не можна нескінченно виплачувати старі борги за рахунок новихШаблон:Sfn:

$\underset{t\to \mathrm{\infty }}{\lim }{a}_t{e}^{-\underset{0}{\overset{t}{\int }}(r(\nu )-n)d\nu }\ge 0$ ,

де $a_t=\frac{K_t}{L_t}=k_t$ — у закритій економіці весь капітал належить резидентам, а величина активів індивіда $a$ збігається із запасом капіталу на одного працівника $k$.

Передумова про закриту економіку означає, що вироблений продукт витрачається на інвестиції та споживання, експорт та імпорт відсутні, заощадження дорівнюють інвестиціям: $S=I$, $Y=C+I$Шаблон:Sfn.

Виробнича функція $Y(K,L,E)$ задовольняє неокласичним передумовамШаблон:SfnШаблон:Sfn:

1) технологічний прогрес збільшує продуктивність праці (нейтральний за Харродом): $Y_t=Y(K_t,L_t{E}_t),E_t=e^{gt},g=const$.

2) у виробничій функції використовуються праця $L$ та капітал $K$, вона має сталу віддачу від масштабу: $Y(aK,aLE)=aY(K,LE)$.

3) гранична продуктивність факторів додатна та спадна: $\frac{\partial Y}{\partial K}>0,\frac{{\partial }^{2}Y}{\partial K^2}<0,\frac{\partial Y}{\partial L}>0,\frac{{\partial }^{2}Y}{\partial L^2}<0$.

4) виробнича функція задовольняє умовам Інади, а саме, якщо запас одного з факторів нескінченно малий, то його гранична продуктивність нескінченно велика, якщо запас одного з факторів нескінченно великий, то його гранична продуктивність нескінченно мала:$\underset{K\to 0}{\lim }\frac{\partial Y}{\partial K}=\underset{L\to 0}{\lim }\frac{\partial Y}{\partial L}=+\mathrm{\infty },\underset{K\to +\mathrm{\infty }}{\lim }\frac{\partial Y}{\partial K}=\underset{L\to +\mathrm{\infty }}{\lim }\frac{\partial Y}{\partial L}=0$.

5) для виробництва необхідний кожен фактор: $Y(K,0)=Y(0,LE)=0$.

Населення $L_t$, що дорівнює в моделі сукупним трудовим ресурсам, зростає зі сталим темпом $n$Шаблон:Sfn: $L_t=e^{nt},n=const$Шаблон:Sfn.

Індивід пропонує одну одиницю праці (пропозиція праці нееластична) та отримує натуральну заробітну плату (в одиницях товару). Функція корисності індивіда-споживача, що живе нескінченно, має виглядШаблон:SfnШаблон:Sfn:

$U=\underset{0}{\overset{\mathrm{\infty }}{\int }}u(c_t)e^{-(\rho -n)t}dt$,

де $c_t=\frac{C_t}{L_t}$ — споживання на душу населення в момент часу $t$; $\rho$ — коефіцієнт міжчасової переваги споживача, $\rho >0,\rho =const$.

Функція корисності $u(c_t)$ сепарабельна, тобто споживання минулих та майбутніх періодів не впливають на поточну корисність, впливає лише споживання поточного періоду. Вона задовольняє умовам $u^{\prime }(c)>0,u^{″}(c)<0$ і умовам Інади (при споживанні, що прямує до нуля, гранична корисність прямує до нескінченності, при споживанні, що прямує нескінченності, гранична корисність прямує до нуля)Шаблон:SfnШаблон:Sfn: $\underset{c\to 0}{\lim }{u}^{\prime }(c)=+\mathrm{\infty };\underset{c\to \mathrm{\infty }}{\lim }{u}^{\prime }(c)=0$.

Для пошуку розв'язку моделі використовують питомі показники: випуск на одиницю праці $y=\frac{Y}{L}$, випуск на одиницю ефективної праці $\hat{y}=\frac{Y}{LE}$, запас капіталу на одиницю ефективної праці $\hat{k}=\frac{K}{LE}$, споживання на одиницю ефективної праці $\hat{c}=\frac{C}{LE}$Шаблон:Sfn.

Завдання споживача

Доходи індивіда витрачаються або на споживання, або на збільшення активів (заощаджень). Населення зростає темпом $n$ тому активи на одну людину скорочуються з тим самим темпом, тобто швидкість зміни активів у кожний момент часу зменшується на $n{a}_t$. Таким чином, похідна активів за часом $\dot{a}$, що виступає як бюджетне обмеження індивіда, має виглядШаблон:Sfn:

$\dot{a}=w_t+r_t{a}_t-c-n{a}_t$.

Задача споживача полягає в максимізації корисності $U$ за бюджетного обмеження та за обмеження на відсутність схеми Понці. Оскільки бюджетне обмеження подано як похідну за часом, то задачу споживача подано як задачу динамічної оптимізації. Її розв'язок можна знайти, побудувавши функцію Гамільтона та знайшовши її максимум за допомогою принципу максимуму ПонтрягінаШаблон:SfnШаблон:Sfn.

Функція Гамільтона має такий вигляд:

$H=u(c)e^{-(\rho -n)t}+{\lambda }_t(w_t+r_t{a}_t-c-n{a}_t)$

за умови:

$\underset{t\to \mathrm{\infty }}{\lim }{a}_t{e}^{-\underset{0}{\overset{t}{\int }}(r(\nu )-n)d\nu }\ge 0$.

Умова максимуму першого порядку: $\frac{\partial H}{\partial c}=u^{\prime }(c)e^{-(\rho -n)t}-{\lambda }_t=0$.

Фазова координата (спряжене рівняння): $\frac{\partial H}{\partial a}=(r_t-n){\lambda }_t=-\dot{\lambda }$, де $\dot{\lambda }$ — похідна $\lambda$ за часом.

Умова трансверсальності (за невиконання якої знайдений розв'язок може виявитися не максимумом, а сідловою точкою): $\underset{t\to \mathrm{\infty }}{\lim }{\lambda }_t{a}_t=0$, де ${\lambda }_t$ — Шаблон:Iw активівШаблон:Sfn (тіньові ціни враховують зовнішні ефекти у вартості товарів, якщо фірми та споживачі приймають рішення відповідно до структури цін, пропорційної тіньовій, то в економіці досягається оптимальний за Парето стан). У цьому випадку умова трансверсальності збігається з обмеженням на відсутність схеми ПонціШаблон:SfnШаблон:Sfn.

Шуканий розв'язок має виглядШаблон:SfnШаблон:Sfn:

$r_t-n=\rho -n-\left(\frac{u^{″}(c)}{u^{\prime }(c)}c\right)\frac{\dot{c}}{c}$ ,

де $\dot{c}$ — похідна споживання за часом, $\frac{u^{″}(c)}{u^{\prime }(c)}c$ — еластичність граничної корисності за споживанням.

Оскільки для подальшого аналізу необхідно, щоб ця величина була сталою, вводиться додаткова передумова про вигляд функції корисності: на її роль беруть функцію з постійною еластичністю заміщенняШаблон:Sfn:

$u(c)=\frac{c^{1-\theta }-1}{1-\theta }$.

У такому разі, $\frac{u^{″}(c)}{u^{\prime }(c)}c=-\theta$, а отжеШаблон:Sfn:

$\frac{\dot{c}}{c}=\frac{1}{\theta }(r_t-\rho )$ ,

де $\dot{c}$ — похідна споживання на душу населення за часом.

Знайдений розв'язок називають правилом Кейнса — Ремзі. Його отримав Френк Ремзі, а змістовну інтерпретацію йому дав Джон КейнсШаблон:SfnШаблон:Sfn.

Задача фірми

Виробничу функцію $Y=f(K,LE)=f(\hat{k})LE$ можна записати через питомі показники: $\hat{y}=f(\hat{k})$. Шаблон:Нп полягає в максимізації прибутку $\pi$Шаблон:Sfn:

$\pi =f(K_t,L_t{E}_t)-(r+\delta )K_t-w{L}_t=L_t{E}_t(f(\widehat{k_t})-(r+\delta )\widehat{k_t}-\frac{w}{E_t})\to \max$

Оскільки фірми діють в умовах досконалої конкуренції, то граничні продуктивності факторів виробництва дорівнюють їхнім цінамШаблон:SfnШаблон:Sfn:

$\frac{\partial Y_t}{\partial K}=f^{\prime }(\widehat{k_t})=r_t+\delta$,

$\frac{\partial Y_t}{\partial L}=(f(\widehat{k_t})-\widehat{k_t}{f}^{\prime }(\widehat{k_t}))e^{gt}=w_t$.

Загальна економічна рівновага

Модель Ремзі — Касса — Купманса, фазова площина

Модель Ремзі — Касса — Купманса, динаміка норми заощаджень

Враховуючи що $a=k$, підставивши отримані з розв'язку задачі фірми значення $r$ і $w$ в рівняння динаміки активів, отримаємоШаблон:Sfn:

$\dot{\hat{k}}=f(\widehat{k_t})-\hat{c}-(\delta +n+g)\widehat{k_t}$.

Оскільки $\frac{\dot{\hat{c}}}{\hat{c}}=\frac{\dot{c}}{c}-g$Шаблон:Sfn, розв'язок задачі споживача можна записати в такому виглядіШаблон:Sfn:

$\frac{\dot{\hat{c}}}{\hat{c}}=\frac{1}{\theta }(r_t-\rho -g\theta )=\frac{1}{\theta }(f^{\prime }(\widehat{k_t})-\delta -\rho -\theta g)$.

У стаціонарному стані $\dot{\hat{c}}=\dot{\hat{k}}=\dot{\hat{y}}=0$. Звідки отримуємо, що $f^{\prime }(\widehat{k_t})=\delta +\rho +\theta g$. У результаті стійкий стан описує система рівняньШаблон:SfnШаблон:Sfn:

$\{\begin{array}{c}{\hat{c}}^{*}=f({\hat{k}}^{*})-(\delta +n+g){\hat{k}}^{*},\\ f^{\prime }({\hat{k}}^{*})=\delta +\rho +\theta g,\end{array}$

де ${\hat{c}}^{*}$ — споживання, а ${\hat{k}}^{*}$ — капіталоозброєність на одиницю ефективної праці в стійкому стані.

За умовою трансверсальностіШаблон:Sfn:

$\underset{t\to \mathrm{\infty }}{\lim }\left({\hat{k}}_t{e}^{-\underset{0}{\overset{t}{\int }}(f^{\prime }({\hat{k}}_{\nu })-\delta -g-n)d\nu }\right)=0$,

звідки випливає $f^{\prime }(\hat{k})>\delta +n+g$. З урахуванням рівняння для $\frac{\dot{\hat{c}}}{\hat{c}}$, ця умова означає, що для існування стійкого стану необхідно, щоб $\rho +\theta g>g+n$. Також це означає, що в моделі Ремзі — Касса — Купманса накопичення капіталу нижче, ніж рівень, що максимізує споживання (модифіковане золоте правило: $\frac{\partial f({\hat{k}}^{**})}{\partial k}=\delta +n+g$, де ${\hat{k}}^{**}$ — капіталоозброєність на одиницю ефективної праці, що відповідає золотому правилу), а значить, неможлива динамічна неефективність у вигляді надмірного накопичення капіталуШаблон:SfnШаблон:Sfn.

Досягнення рівноваги моделі можна проілюструвати за допомогою фазової площини. Лінії $\dot{\hat{c}}=0$ і $\dot{\hat{k}}=0$ ділять діаграму на чотири квадранти. Ліворуч від лінії $\dot{\hat{c}}=0$ траєкторія капіталоозброєності йде вгору, а праворуч від лінії $\dot{\hat{c}}=0$ — вниз. Вище від лінії $\dot{\hat{k}}=0$ траєкторія капіталоозброєності йде вліво, а нижче від лінії $\dot{\hat{k}}=0$ — вправо. Таким чином, у квадранті I траєкторія йде вліво і вгору, в квадранті II -— вліво і вниз, у квадранті III — вправо і вниз, в квадранті IV — вправо та вгору. У результаті, в моделі існує лише одна траєкторія, що веде до рівноваги — зелена лінія на ілюстрації. На цій лінії розташована множина точок ${\hat{c}}_0$ і ${\hat{k}}_0$, із яких система входить у стійкий стан. Варіанти траєкторії з інших точок показано червоним, у цьому випадку зрештою стає рівною нулю або капіталоозброєність ($\hat{k}=0$), або споживання ($\hat{c}=0$)Шаблон:Sfn. Оскільки оптимальна траєкторія капіталоозброєності в моделі має вигляд сідла, її також називають «сідловим шляхом»Шаблон:Sfn.

Модель передбачає наявність умовної конвергенції, тобто, що країни з малим рівнем капіталоозброєності зростатимуть вищими темпами, ніж із великим рівнем капіталоозброєності $k$, за умови, що стійкий стан у них однаковий. Швидкість наближення до стійкого стану можна оцінити за допомогою лінійної апроксимації за допомогою, розклавши в ряд Тейлора диференціальні рівняння для $\dot{\hat{c}}$ і $\dot{\hat{k}}$Шаблон:Sfn:

У цій моделі рівноваги для централізованої та децентралізованої економік однаковіШаблон:Sfn.

Конвергенція

Вплив фіскальної політики на рівновагу проілюстровано фазовою площиною.

$\{\begin{array}{c}\dot{\hat{c}}\approx \frac{\partial \dot{\hat{c}}}{\partial \widehat{k_t}}{|}_{\widehat{k_t}={\hat{k}}^{*}}(\widehat{k_t}-{\hat{k}}^{*})+\frac{\partial \dot{\hat{c}}}{\partial \widehat{c_t}}{|}_{\widehat{c_t}={\hat{c}}^{*}}(\widehat{c_t}-{\hat{c}}^{*}),\\ \dot{\hat{k}}\approx \frac{\partial \dot{\hat{k}}}{\partial \widehat{k_t}}{|}_{\hat{k}={\hat{k}}^{*}}(\widehat{k_t}-{\hat{k}}^{*})+\frac{\partial \dot{\hat{k}}}{\partial {\hat{c}}_t}{|}_{\widehat{c_t}={\hat{c}}^{*}}(\widehat{c_t}-{\hat{c}}^{*}).\end{array}$

З умов стійкості випливає, що кутовий коефіцієнт у другого доданку ($c_t-{\hat{c}}^{*}$) в другому рівнянні дорівнює -1, а в першому — 0. Скориставшись рівнянням стійкого стану, можна записати лінійні апроксимації в такому виглядіШаблон:Sfn:

$\{\begin{array}{c}\dot{\hat{c}}\approx \frac{f^{″}({\hat{k}}^{*})\hat{c}}{\theta }(\widehat{k_t}-{\hat{k}}^{*}),\\ \dot{\hat{k}}\approx (\rho +\theta g-g)(\widehat{k_t}-{\hat{k}}^{*})-(\widehat{c_t}-{\hat{c}}^{*}).\end{array}$

Розв'язок цієї системи рівнянь має виглядШаблон:Sfn:

$\{\begin{array}{c}{\hat{k}}_t-{\hat{k}}^{*}=({\hat{k}}_0-{\hat{k}}^{*})e^{\mu t},\\ {\hat{c}}_t-{\hat{c}}^{*}=({\hat{c}}_0-{\hat{c}}^{*})e^{\mu t},\end{array}$

де $\mu$ — коефіцієнт, що характеризує швидкість конвергенції.

Розрахунки швидкості конвергенції за моделлю Ремзі — Касса — Купманса з використанням параметрів, близьких до параметрів економіки США, передбачають високу швидкість конвергенції, що не спостерігається на реальних данихШаблон:Sfn.

Фіскальна політика в моделі

Модель Ремзі — Касса — Купманса, фазова площина, фіскальна політика

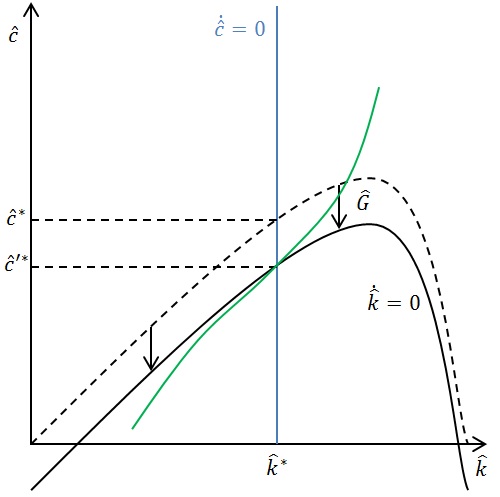
Модель дозволяє оцінити вплив на рівновагу фіскальної політики. Вважається, що величина податків дорівнює величині державних витрат, які не впливають на корисність індивідів і майбутній випуск. У цьому випадку рівняння для $\dot{\hat{k}}$ набуде такого виглядуШаблон:Sfn:

$\dot{\hat{k}}=f(\widehat{k_t})-\hat{c}-\hat{G}-(\delta +n+g)\widehat{k_t}$,

де $\hat{G}$ — величина державних витрат на одиницю праці зі сталою ефективністю.

Внаслідок фіскальної політики крива $\dot{\hat{k}}=0$ зсувається вниз на величину $\hat{G}$ і рівновага в моделі встановлюється на колишньому рівні капіталоозброєності, але споживання знижується на величину $\hat{G}$. Таким чином, у моделі державні витрати витісняють споживанняШаблон:Sfn.

Найважливіший внесок моделі Ремзі — Касса — Купманса полягає в тому, що вона розкрила механізм формування норми заощаджень через рішення споживачів, а також стала основою для подальшого аналізу того, як рішення індивідів формують накопичення фізичного та людського капіталу, і, як наслідок, науково-технічний прогрес. Це стало великим кроком уперед, порівняно з моделлю Солоу, і значною мірою з цієї причини модель стала відправною точкою для багатьох дослідників, які використовували її концептуальний та математичний апарат для побудови власних моделейШаблон:Sfn. Неокласичну модель економічного зростання розглядають у всіх сучасних підручниках макроекономіки та теорії економічного зростанняШаблон:Sfn.

Переваги, недоліки та подальший розвиток моделі

Оптимальна динаміка споживання з моделі (правило Кейнса — Ремзі) виявилася вдалою заміною екзогенної норми заощаджень і потім застосовувалася і в пізніших моделях економічного зростання, де економічним агентом виступає індивід, який живе нескінченно (або домогосподарство): в Шаблон:Нп, Шаблон:Нп, Шаблон:Нп, Шаблон:НпШаблон:Sfn.

Включення до моделі зовнішніх ефектів від рівня фізичного та людського капіталу (для чого в деяких випадках довелося відмовитися від 2, 3 та 4 передумов неокласичної виробничої функції) привело до розвитку АК-моделей Шаблон:Sfn .

Шаблон:Нп додав у модель грошову масу, щоб проаналізувати вплив грошової емісії та інфляції на реальні показники економіки. У результаті в розширеній моделі рівновага вийшло такою самою, як і моделі без грошової маси, що означає відсутність впливу пропозиції грошей на реальні показники. Отриману властивість назвали нейтральністю грошейШаблон:Sfn.

Недоліком моделі деякі дослідники вважали нескінченно живого індивіда (або домогосподарство) як вічного споживачаШаблон:Sfn. У міру дорослішання характер споживчої поведінки змінюється. Якщо в молодому віці індивід працює і робить заощадження, то на старості він ці заощадження витрачаєШаблон:Sfn. Цей факт відбито в моделі поколінь, що перетинаються, яка повністю заперечує альтруїстичні зв'язки між поколіннямиШаблон:SfnШаблон:Sfn.

Разом з тим, модель не зробила істотного внеску в розуміння причин міжкраїнних відмінностей у рівні ВВП на душу населення і його зростання. Модель передбачає наявність умовної конвергенції, що означає, що бідні країни повинні зростати швидше від багатих за умови схожості структурних параметрів, але насправді цього не відбувається, як показали, наприклад, дослідження Шаблон:Нп та Шаблон:НпШаблон:Sfn, Дж. Де ЛонгаШаблон:Sfn, П. РомераШаблон:Sfn. Є лише поодинокі приклади (японське економічне диво, корейське економічне диво) коли бідні країни змогли наздогнати багаті за рівнем ВВП на душу населення, здебільшого зближення рівня розвитку не відбуваєтьсяШаблон:Sfn. Так само, як і в моделі Солоу, науково-технічний прогрес у моделі Ремзі — Касса — Купманса не є наслідком прийняття рішень економічними агентами, а задається екзогенноШаблон:Sfn.

У моделі неможлива динамічна неефективність, розв'язки для централізованої та децентралізованої економік однакові, а отже неможлива неоптимальна за Парето рівновага в економіці, тому модель не показує, як неправильна економічна політика або обмежувальні соціальні інституції можуть уповільнити розвиток країни. Іншими словами, модель не пояснює причин, через які бідні країни залишаються бідними і не можуть наздогнати багатихШаблон:Sfn.

Література

• Шаблон:Книга
• Шаблон:Книга
• Шаблон:Книга
• Шаблон:Книга
• Шаблон:Книга
• Шаблон:Стаття
• Шаблон:Стаття
• Шаблон:Стаття
• Шаблон:Стаття
• Шаблон:Стаття
• Шаблон:Стаття
• Шаблон:Стаття
• Шаблон:Стаття
• Шаблон:Стаття
• Шаблон:Стаття
• Шаблон:Стаття