Зрізаний куб

Файл:Truncated cube.stl

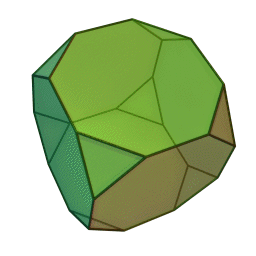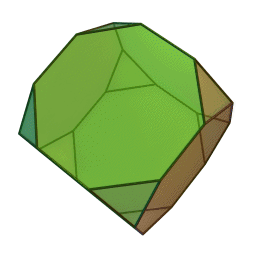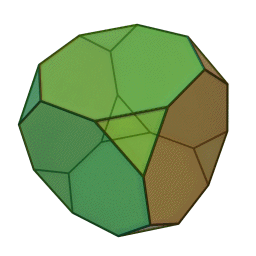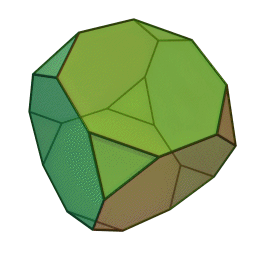
Зрі́заний куб або ж зрі́заний гекса́едр — напівправильний многогранник, відноситься до архімедових тіл, що складається із 6-и правильних восьмикутників і 8-и правильних трикутників, 36-и ребер і 24-х кутів. Двоїстий до зрізаного куба многогранник — триакісоктаедр.

Отримати даний многогранник можна за рахунок зрізання всіх чотирьох вершин куба на третину від первісної довжини ребра.

Ортогональні проєкції. Зрізаний куб має п'ять спеціальних ортопроєкцій - по центру, на вершині, на двох типах ребер, і двох типах площин: трикутниках і восьмикутниках.

Формули

Знаючи довжину ребра зрізаного куба - a - отримуємо:

Математичний опис
Об'єм	$V=\frac{1}{3}(21+14\sqrt{2})a^3\approx 13.5996633a^3.$
Площа поверхні	$S=2(6+6\sqrt{2}+\sqrt{3})a^2\approx 32.4346644a^2$

Графічне зображення

Розгортка зрізаного куба

Сферична плитка

Зрізаний куб можна подати у вигляді сферичної плитки, і спроєктувати на площину у вигляді стереографічної проєкції. Ця проєкція буде конформною, зберігаючи кути, але не площини чи ребра багатогранника. Прямі лінії на сфері проєктуватимуться як дуги на площині.

	центрована восьмикутником	центрована трикутником
Сферична плитка	Стереографічна проєкція

Джерела

• Шаблон:MathWorld
• Пчелінцев В.О. Кристалографія, кристалохімія та мінералогія. Навчальний посібник для студентів вищих навчальних закладів. Суми: Вид-во СумДУ, 2008, - 232с.
• Гордєєва Є.П., Величко В.Л. Нарисна геометрія. Багатогранники (правильні, напівправильні та зірчасті). Частина І. Навчальний посібник. Луцьк: Редакційно-видавничий відділ ЛДТУ, 2007, – 198с.
• П. С. Александрова, А. И. Маркушевича и А. Я. Хинчина. Многоугольники и многогранники. Энциклопедия элементарной математики. Москва: Государственное издательство физико-математической литературы, 1963, - 568с.