Теорема Гюйгенса — Штейнера

Ілюстрація до теореми Гюйгенса-Штейнера.

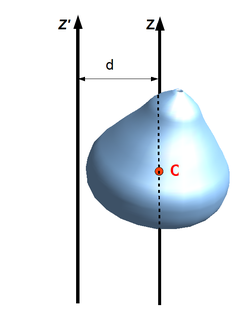
Теоре́ма Гю́йгенса — Штейнера, або теорема Штейнера (названа іменами швейцарського математика Якова Штейнера і нідерландського математика, фізика і астронома Хрістіана Гюйгенса): момент інерції тіла $I_z$ відносно довільної осі дорівнює сумі моменту інерції цього тіла $I_{cm}$ відносно осі, що проходить через центр маси тіла паралельно до осі, що розглядається і добутку маси тіла $m$ на квадрат відстані $d$ між осями:

$I_z=I_{cm}+m{d}^2$.

Момент інерції досягає свого мінімального значення, коли вісь проходить через центр мас.

Наприклад, момент інерції стрижня відносно осі, що проходить через його кінець, становить:

$J=J_0+m{d}^2=\frac{1}{12}m{l}^2+m{\left(\frac{l}{2}\right)}^2=\frac{1}{3}m{l}^2$

Перерахунок тензора моменту інерції

Теорема Гюйгенса — Штейнера допускає узагальнення на тензор моменту інерції, що дозволяє отримати тензор $J_{ij}$ відносно довільної точки з тензора $I_{ij}$ відносно центру мас. Нехай d — зміщення від центру мас, тоді

$J_{ij}=I=I_{ij}+m\left(\begin{array}{ccc}{d}_2^2+d_3^2& -d_1{d}_2& -d_1{d}_3\\ -d_1{d}_2& d_1^2+d_3^2& -d_2{d}_3\\ -d_1{d}_3& -d_2{d}_3& d_1^2+d_2^2\end{array}\right)=I_{ij}+M({𝒅}^2{\delta }_{ij}-d_i{d}_j)$

де

$𝒅=d_1\widehat{𝒙}+d_2\widehat{𝒚}+d_3\widehat{𝒛}$ — вектор зміщення від центру мас,

${\delta }_{ij}$ — символ Кронекера.

Як видно, для діагональних елементів тензора (при i = j) формула набуде вигляду теореми Гюйгенса-Штейнера для перерахунку моменту інерції відносно паралельної осі.

Доведення

Будемо розглядати абсолютно тверде тіло, утворене сукупністю матеріальних точок.

Згідно визначення моменту інерції для $J_c$ та $J$ можна записати :

$Jc=\sum _{i=1}^n{m}_i(r_i{)}^2$,

$J=\sum _{i=1}^n{m}_i(r_i^{\text{'}}{)}^2$,

де $r$ — радіус-вектор точки тіла в системі координат з початком, який знаходиться в центрі мас, а $r^{\prime }$ — радіус-вектор точки нової системи координат, через початок якої проходить нова вісь.

Радіус-вектор можна розписати як суму двох векторів :

$r{\text{'}}_i=r_i+d$ ,

де $d$ — радіус-вектор відстаней між старою (яка проходить через центр масс) і новою віссю обертання. Тоді вираз для момента інерції набуде вигляду :

$J=\sum _{i=1}^n{m}_i(r_i{)}^2+2\sum _{i=1}^n{m}_i{r}_{i}d+\sum _{i=1}^n{m}_i(d{)}^2$.

Винісши d за суму, отримаємо :

$J=\sum _{i=1}^n{m}_i(r_i{)}^2+2d\sum _{i=1}^n{m}_i{r}_i+d^2\sum _{i=1}^n{m}_i$ .

Згідно визначення центру мас, для його радіус-вектора виконується

$r_c=\frac{\sum _i{m}_i{r}_i}{\sum _i{m}_i}$ ,

Оскільки в системі координат з початком, який знаходиться в центрі масс, радіус-вектор дорівнює нулю, то буде виконуватися наступна рівність :

$\sum _{i=1}^n{m}_i{r}_i=0$ ,

Тоді :

$J=\sum _{i=1}^n{m}_i(r_i{)}^2+d^2\sum _{i=1}^k{m}_i$ ,

звідки і слідує шукана формула :

$J=J_c+m{d}^2$ ,

де $J_c$ — відомий момент інерції відносно осі, яка проходить через центр мас тіла.

Якщо тіло складається не із матеріальних точок, а утворено неперервно розподіленою масою, то в усіх вище наведених формулах сумування змінюється на інтегрування. Доведення при цьому є ідентичним, лише за винятком того, що буде інтеграл, а не сума.

Наслідок: з отриманої формули очевидно, що $J>J_c$. Тому можна стверджувати, що момент інерції тіла відносно осі, який проходить через центр мас тіла, є найменшим серед всіх моментів інерцій тіла відносно осей, які мають аналогічний напрям.

Див. також

• Момент інерції
• Теорема перпендикулярних осей

Література

• Павловський М. А. Теоретична механіка: Підручник для студентів вищих навчальних закладів.- К.: Техніка,2002.- 512 с. ISBN 966-575-184-0.
• Цасюк В. В. Теоретична механіка: Навчальний посібник.- К.: ЦУЛ, 2004.- 402 с. ISBN 966-8253-79-5
• Федорченко А. М. Теоретична механіка.- Київ: Вища школа, 1975. — 516 с.

Посилання

• Parallel axis theorem