Опукла оптимізація

Шаблон:UniboxОпукла оптимізація — це підрозділ математичної оптимізації, котрий вивчає проблему мінімізації опуклих функцій над опуклими множинами. Багато класів задач з опуклою оптимізацією допускають поліноміальні алгоритми тоді як математична оптимізація в цілому NP-важка.

Опукла оптимізація має застосування в широкому спектрі дисциплін, таких як автоматичні системи управління, оцінка та обробка сигналів, комунікації та мережі, проєктування електронних схем, аналіз та моделювання даних, фінанси, статистика (оптимальний експериментальний дизайн), та структурна оптимізація, де концепція наближення виявилась ефективною. З недавніми досягненнями в галузі обчислювальних та оптимізаційних алгоритмів, опукле програмування майже настільки ж просте, як і лінійне програмування.

Визначення

Проблема оптимізації опуклості — це проблема оптимізації, в якій цільова функція є опуклою функцією, а допустимою множиною є опукла множина. Функція $f$ відображення деякої підмножини ${ℝ}^n$ в $ℝ\cup \{\pm \mathrm{\infty }\}$ опукла, якщо її домен опуклий і для всіх $\theta \in [0,1]$ і також для всіх $x,y$ у своєму домені виконується така умова: $f(\theta x+(1-\theta )y)\le \theta f(x)+(1-\theta )f(y)$. Множина S опукла, якщо для всіх членів $x,y\in S$ і для всіх $\theta \in [0,1]$, у нас є, що $\theta x+(1-\theta )y\in S$.

Конкретно, проблема опуклої оптимізації — це проблема пошуку ${𝐱}^{\mathbf{\ast }}\in C$ маючи

$\inf \{f(𝐱):𝐱\in C\}$,

де об'єктивна функція $f$ є опуклою, як і допустима множина $C$. Якщо така точка існує, вона називається оптимальною точкою ; множина всіх оптимальних точок називається оптимальною множиною. Якщо $f$ є необмеженою внизу над $C$ або мінімум не досягнуто, тоді, як кажуть, проблема оптимізації є необмеженою. Інакше, якщо $C$ є порожньою множиною, тоді проблема, як кажуть, невирішувана.

Стандартна форма

Кажуть, що проблема опуклої оптимізації є в стандартній формі, якщо вона записана як

$\begin{array}{cccc}& \underset{𝐱}{\mathrm{minimize}}& & f(𝐱)\\ & \mathrm{s}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{t}\mathrm{o}& & g_i(𝐱)\le 0,i=1,\dots ,m\\ & & & h_i(𝐱)=0,i=1,\dots ,p,\end{array}$

де $x\in {ℝ}^n$ — змінна оптимізації, функції $f,g_1,\dots ,g_m$ є опуклими, і функції $h_1,\dots ,h_p$ є афінними. У цьому позначенні функція $f$ — це цільова функція задачі, і функції $g_i$ і $h_i$ називаються функціями обмеження. Можливим набором задачі оптимізації є множина, що складається з усіх точок $x\in {ℝ}^n$ задовольняючи $g_1(x)\le 0,\dots ,g_m(x)\le 0$ і $h_1(x)=0,\dots ,h_p(x)=0$. Ця множина є опуклою, оскільки підмножини опуклих функцій опуклі, афінні множини опуклі, а перетин опуклих множин — опуклий.

Багато проблем оптимізації можуть бути сформульовані в цій стандартній формі. Наприклад, проблема максимізації увігнутої функції $f$ може бути переформульовано як проблема мінімізації опуклої функції $-f$ ; така проблема максимізації увігнутої функції над опуклою множиною часто називається проблемою оптимізації опуклої форми.

Властивості

Наступні корисні властивості задач опуклої оптимізації:

• кожен локальний мінімум — це глобальний мінімум;
• оптимальна множина опукла;
• якщо цільова функція строго опукла, то задача має щонайменше одну оптимальну точку.

Ці результати використовуються теорією опуклої мінімізації разом з геометричними поняттями функціонального аналізу (в просторах Гільберта), такими як теорема проєкції Гільберта, теорема розділення гіперплан та лема Фаркаса.

Приклади

Перелічені класи задач — це все задачі опуклої оптимізації, або їх можна звести до задачі опуклої оптимізації за допомогою простих перетворень:

Ієрархія задач опуклої оптимізації. (LP: лінійна програма, QP: квадратична програма, програма конусів SOCP другого порядку, SDP: напіввизначена програма, CP: програма конуса.)

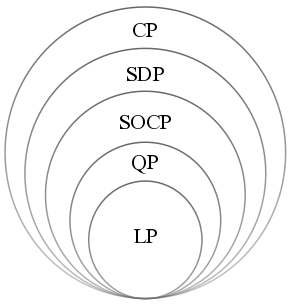
• Найменші квадрати
• Лінійне програмування
• Опукла квадратична мінімізація з лінійними обмеженнями
• Квадратна мінімізація з опуклими квадратичними обмеженнями
• Конічна оптимізація
• Геометричне програмування
• Програмування конуса другого порядку
• Напівскінченне програмування
• Максимізація ентропії з відповідними обмеженнями

Множники Лагранжа

Розглянемо проблему мінімізації опуклої форми, задану в стандартній формі функцією витрат $f(x)$ та обмеженням нерівності $g_i(x)\le 0$ для $1\le i\le m$. Домен $𝒳$ є:

$𝒳=\{x\in X|g_1(x),\dots ,g_m(x)\le 0\}.$

Функцією Лагранжа для задачі є

$L(x,{\lambda }_0,{\lambda }_1,\dots ,{\lambda }_m)={\lambda }_{0}f(x)+{\lambda }_1{g}_1(x)+\cdots +{\lambda }_m{g}_m(x).$

Для кожної точки $x$ в $X$ що мінімізує $f$ над $X$, існують реальні числа ${\lambda }_0,{\lambda }_1,\dots ,{\lambda }_m,$ котрі називаються множниками Лагранжа, які одночасно задовольняють ці умови:

1. $x$ мінімізує $L(y,{\lambda }_0,{\lambda }_1,\dots ,{\lambda }_m)$ над усім $y\in X,$
2. ${\lambda }_0,{\lambda }_1,\dots ,{\lambda }_m\ge 0,$ принаймні з одним ${\lambda }_k>0,$
3. ${\lambda }_1{g}_1(x)=\cdots ={\lambda }_m{g}_m(x)=0$ (додаткова млявість).

Якщо існує «строго допустима точка», тобто точка $z$, котра задовольняє

$g_1(z),\dots ,g_m(z)<0,$

тоді твердження вище може вимагати ${\lambda }_0=1$.

І навпаки, якщо якісь $x$ в $X$ задовольняють (1) — (3) для скалярів ${\lambda }_0,\dots ,{\lambda }_m$ з ${\lambda }_0=1$, то $x$ мінімізує $f$ над $X$.

Алгоритми

Задачі опуклої оптимізації можуть бути розв'язані такими сучасними методами:

• Методи розшарування (Вулф, Лемарель, Ківіль) та
• Методи субградієнтної проєкції (Поляк),
• Методи внутрішніх точок, в яких використовуються самокорегуючі бар'єрні функції та саморегулярні бар'єрні функції.
• Ріжучі площинні методи
• Еліпсоїдний метод
• Субградієнтний метод
• Подвійні субградієнти та метод дрейфу плюс-штраф

Субградієнтні методи можуть бути реалізовані просто і тому широко застосовуються. Подвійні субградієнтні методи — це субградієнтні методи, застосовані до подвійної задачі. Метод дрейфування плюс-штрафу схожий з методом подвійного субградієнта.

Розширення

Розширення опуклої оптимізації включають оптимізацію функцій двоопуклої, псевдоопуклої та квазіопуклої. Розширення теорії опуклого аналізу та ітеративних методів приблизно розв'язування задач мінімізації, що не є опуклими, відбуваються в області узагальненої опуклості, також відомої як абстрактний опуклий аналіз.

Див. також

• Двоїстість (оптимізація)
• Умови Каруша — Куна — Такера
• Задача оптимізації
• Метод проксимального градієнта
• Алгоритм Франк — Вульфа

Список літератури

• Шаблон:Cite book
• Шаблон:Cite book
• Шаблон:Cite book
• Шаблон:Cite book
• Борвейн, Джонатан та Льюїс, Адріан. (2000). Аналіз опуклості та нелінійна оптимізація. Спрингер.
• Шаблон:Cite book Шаблон:Cite book Шаблон:Cite book
• Хіріарт-Урруті, Жан-Батист і Лемарешал, Клод. (2004). Основи опуклого аналізу. Берлін: Спрінгер.
• Шаблон:Cite book Шаблон:Cite book Шаблон:Cite book
• Шаблон:Cite book Шаблон:Cite book Шаблон:Cite book
• Шаблон:Cite book Шаблон:Cite book Шаблон:Cite book
• Шаблон:Cite book Шаблон:Cite book Шаблон:Cite book
• Шаблон:Cite book
• Нестеров, Юрій. (2004). Вступні лекції з опуклої оптимізації, наукові видавці Kluwer
• Шаблон:Cite book
• Шаблон:Cite book
• Шміт, Л.А.; Флері, C. 1980: Структурний синтез шляхом поєднання концепцій наближення та подвійних методів. Дж. Амер. Інст. Аеронавт. Астронавт 18, 1252—1260

Посилання

• Стівен Бойд та Лівен Ванденберге, опукла оптимізація (книга в pdf)
• EE364a: Опукла оптимізація I та EE364b: Опукла оптимізація II, домашні сторінки курсу «Стенфорд»
• 6.253: Опуклий аналіз та оптимізація, домашня сторінка курсу MIT OCW
• Брайан Борчерс, Огляд програмного забезпечення для опуклої оптимізації