Крайова задача

Крайова задача — задача теорії диференціальних рівнянь, в якій межові умови задаються в різних точках. Наприклад, при коливаннях струни із закріпленеми кінцями зміщення на кожному з кінців дорівнює нулю.

Крайові задачі складніше розв'язувати, ніж задачі Коші, особливо чисельно.

Крайові задачі виникають як у теорії звичайних диференціальних рівнянь, так і в теорії диференціальних рівнянь з частинними похідними, особливо рівнянь еліптичного типу.

Особливий вид крайової задачі — вимога певної поведінки функції (скінченності) при прямуванні аргументу до нескінченності або в околі особливих точок.

Нехай $\mathrm{\Omega }$ — область на площині $x,y$ із межею $\mathrm{\Gamma }.$

Важливими задачами є:

• $u(x,y){|}_{(x,y)\in \mathrm{\Gamma }}=\phi (x,y)$ — перша крайова задача, задача Діріхле

• $\frac{\partial u(x,y)}{\partial n}{|}_{(x,y)\in \mathrm{\Gamma }}=\phi (x,y)=\psi (x,y)$ — друга крайова задача, задача Неймана

• $au(x,y)+b\frac{\partial u(x,y)}{\partial n}=\chi (x,y)$ для $(x,y)$ на $\mathrm{\Gamma }$ — третя крайова задача, задача Робена
  

Методи розв'язування крайових задач

Метод сіток

Розглядається не континуум точок площини $x,y,$ а зліченна множина дискретних точок ${\mathrm{\Pi }}_{ij}=(x_i,y_i).$

Якщо область $\mathrm{\Omega }$ розмістити на сітці, то одні точки сітки попадуть усередину, а інші виявляться зовні області. Дискретна ${\mathrm{\Omega }}^{*}$ область складається з точок сітки, які лежать усередині області $\mathrm{\Omega }$, точки сітки, найближчі до межі й які лежать або всередині, або зовні (це залежить від постановки задачі), розраховують як точки дискретної межі ${\mathrm{\Gamma }}^{*}.$ У цьому випадку дискретна область ${\tilde{\mathrm{\Omega }}}^{*}={\mathrm{\Omega }}^{*}\bigcup \mathrm{\Gamma }$ складається лише з точок сітки.

Друга можливість полягає в тому, що додають точки перетину $\mathrm{\Gamma }$ із прямими сітки як нерегулярні граничні точки.

Похідні, які зустрічаються у розглядуваному диференціальному рівнянні, замінюють у кожній точці сітки ${\mathrm{\Pi }}_{ij}=(x_i,y_i)$ відповідними різнісними відношеннями. Наприклад,

$\frac{\partial u}{\partial n}{|}_{ij}=\frac{1}{2h}(-u_{i-1,j}+u_{i+1,j})+O(h^2).$

Такі вирази називають також молекулами й записують у вигляді наочних структурних формул.

П'ятиточкові молекули для оператора Лапласа (квадратна сітка):

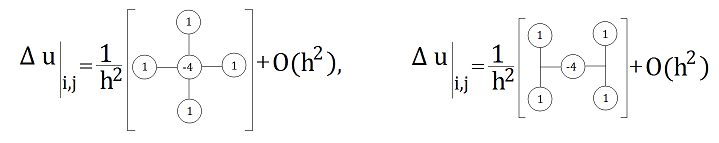
Якщо область $\mathrm{\Omega }$ така, що для достатньо простої сітки за відповідно вибраного розташування межа $\mathrm{\Gamma }$ складається лише з сіткових прямих, то крайові значення задаються у граничних сіткових точках й уводяться відповідні молекули, якщо вони включають такі точки.

Наприклад, рівняння Пуассона у прямокутнику

$\mathrm{\Omega }=\{(x,y)|0\le x\le 4k,0\le y\le 3h\}.$

Сітка $(x_i,y_i)=(ik,jh),$

${\mathrm{\Omega }}^{*}=\{(ik,jh)|0\le i\le 4,4\le j\le 3\}$ — регулярна межа.

Нехай $\mathrm{\Omega }$ є областю на площині $x,y$ із межею $\mathrm{\Gamma }.$ Потрібно відшукати функцію $u(x,y),$ яка задовольняє $\mathrm{\Omega }$ рівняння Пуассона

$\mathrm{\Delta }u=u_{xx}^{\prime \prime }+u_{yy}^{\prime \prime }=g(x,y).$

При застосуванні молекули ліворуч

$U_{i-1,j}+U_{i+1,j}+U_{i,j-1}+U_{i,j+1}-4U_{ij}=h^2{f}_{ij}$

як дискретний аналог рівняння Пуассона (через $U_{ij}$ позначено наближення для $u(x_i,y_j)=u_{ij}$).

Якщо записати усі рівняння, для яких «центральний елемент» $u_{ij}$ є внутрішньою точкою (тобто $1\le i\le 3,1\le j\le 2$), то

$\underset{\_}{U_{01}}+U_{21}+\underset{\_}{U_{10}}+U_{12}-4U_{11}=h^2{f}_{11}$

$U_{11}+U_{31}+\underset{\_}{U_{20}}+U_{22}-4U_{21}=h^2{f}_{21}$

$U_{21}+\underset{\_}{U_{41}}+\underset{\_}{U_{30}}+U_{32}-4U_{31}=h^2{f}_{31}$

$\underset{\_}{U_{02}}+U_{22}+U_{10}+\underset{\_}{U_{13}}-4U_{12}=h^2{f}_{12}$

$U_{12}+U_{32}+U_{20}+\underset{\_}{U_{23}}-4U_{22}=h^2{f}_{22}$

$U_{22}+\underset{\_}{U_{42}}+U_{30}+\underset{\_}{U_{33}}-4U_{32}=h^2{f}_{32}$

Підкреслені значення можна перенести праворуч.

Тоді дискретним аналогом задачі є система лінійних рівнянь:

$\left(\begin{array}{cccccc}-4& 1& 0& 1& 0& 0\\ 1& -4& 1& 0& 1& 0\\ 0& 1& -4& 0& 0& 1\\ 1& 0& 0& -4& 1& 0\\ 0& 1& 0& 1& -4& 1\\ 0& 0& 1& 0& 1& -4\end{array}\right)\left(\begin{array}{c}{U}_{11}\\ U_{21}\\ U_{31}\\ U_{12}\\ U_{22}\\ U_{32}\end{array}\right)=\left(\begin{array}{c}{h}_{11}^2-U_{01}-U_{10}\\ h^2{f}_{21}-U_{20}\\ h^2{f}_{31}-U_{41}-U_{30}\\ h^2{f}_{12}-U_{02}-U_{13}\\ h^2{f}_{22}-U_{23}\\ h^2{f}_{32}-U_{42}-U_{33}\end{array}\right).$

Для розв'язання таких систем застосовують ітераційні методи, хоча можуть застосовуватися методи, які використовують блокову структуру.

Чисельні

• Метод стрільби

Див. також

• Функції Куранта