Брахістохрона

Шаблон:Unibox Брахістохро́на (Шаблон:Lang-el — найкоротший і Шаблон:Lang-el — час) — крива найшвидшого спуску, тобто та з усіх можливих кривих, що сполучають дві точки А і В (мал.), вздовж якої важка кулька, що ковзає без тертя (або котиться) за відсутності опору середовища з точки А, за найкоротший час досягає нижчої точки В. Брахістохрона — звичайна циклоїда з горизонтальною основою і точкою розвороту у верхній точці А. Задача про брахістохрону, поставлена Йоганном Бернуллі в 1696 році і розв'язана Ісааком Ньютоном в 1697 році, відіграла важливу роль у розвитку варіаційного числення.

Постановка математичної задачі

Рух тіл за різними траєкторіями. Червона лінія — брахістохрона

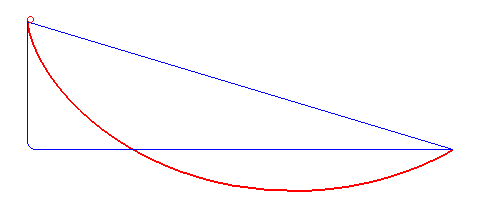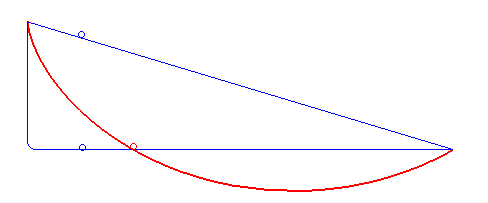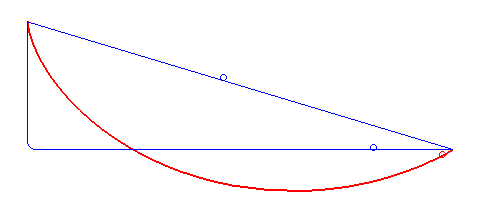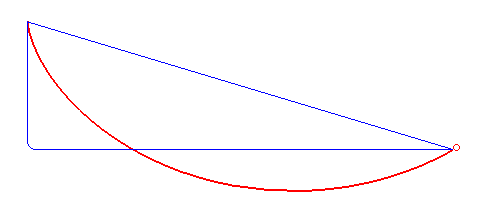
Очевидно, закон збереження енергії накладає обмеження на висоту точки В: точка В має знаходитись нижче, або на тій самій висоті що і точка А. Якщо точка В лежить на одній вертикальній прямій з точкою А, то розв'язок задачі очевидний — траєкторія найшвидшого спуску буде відрізок прямої [АВ]. Тому ми будемо розглядати випадок, коли точка В дещо зміщена від точки А по горизонталі.

Виберемо початок координат $O$ в початковій точці А, і направимо вісь абсцис $Ox$ горизонтально в напрямку кінцевої точки В (допустимо для визначеності малюнка, що ми дивимося на ці точки з таким ракурсом, що точка В знаходиться правіше від точки А), а вісь ординат $Oy$ вертикально вниз. Очевидно, третя просторова координата повинна дорівнювати нулю на кривій найшвидшого спуску (проєкція будь-якої просторової кривої на площину $Oxy$ даватиме менший час спуску).

Оскільки втрати енергії на тертя відсутні, ми можемо записати закон збереження енергії, прийнявши енергію кульки в точці А за нуль:

$(1)0=E_k+U$

Потенціальна енергія кульки масою $m$ в полі тяжіння дорівнює:

$(2)U=-mgy$

Кінетична енергія для кульки що ковзає без обертання (як намистина на дроті) дорівнює:

$(3)E_k=\frac{m{v}^2}{2}$

Якщо ж кулька котиться без проковзування, то до кінетичної енергії поступального руху (3) треба ще додати кінетичну енергію обертання:

$(4)E_{rot}=\frac{I{\omega }^2}{2}$

Для суцільної однорідної кульки радіуса $R$ маємо момент інерції $I=\frac{2}{5}m{R}^2$, а тому кінетична енергія дорівнює:

$(5){\tilde{E}}_k=\frac{m{v}^2}{2}+\frac{m{R}^2{\omega }^2}{5}=\frac{7}{10}m{v}^2$

Підставивши (2) і (3) в (1), одержуємо рівняння:

$(6)\frac{m{v}^2}{2}-mgy=0$

звідки знаходимо швидкість кульки (що ковзає без обертання) в довільній точці кривої:

$(7)v=\sqrt{2gy}$

аналогічно, з (2), (5) і (1) знаходимо швидкість кульки, що котиться:

$(8)\tilde{v}=\sqrt{\frac{10gy}{7}}$

Далі, враховуючи залежність між швидкістю, пройденим шляхом і пройденим часом:

$(9)v=\frac{ds}{dt},dt=\frac{ds}{v}$

Знаходимо, що час руху кульки вздовж кривої від точки А до точки В дається інтегралом ($x_A=0$ через вибір системи координат):

$(10)t=\int dt=\int \frac{ds}{v}=\alpha \int \frac{\sqrt{d{x}^2+d{y}^2}}{\sqrt{y}}=\alpha \underset{0}{\overset{x_B}{\int }}\sqrt{\frac{1+y{\text{'}}^2}{y}}dx$

де постійна $\alpha$ дорівнює відповідно для кульки що ковзає, і для кульки що котиться:

$(11)\alpha =\frac{1}{\sqrt{2g}},\tilde{\alpha }=\sqrt{\frac{7}{10g}}$

Отже, математично задача про брахістохрону формулюється так: нам треба знайти таку невід'ємну функцію, зафіксовану на кінцях:

$(12)y=y(x),x\in [0,x_B];y(0)=0,y(x)\ge 0,y(x_B)=y_B$

що інтеграл у формулі (10) досягає мінімуму. Зауважимо, що константа $\alpha$ не впливає на розв'язок, а тому ми її опускатимемо аж доки не почнемо цікавитися, чому дорівнює цей мінімальний час спуску.

Шукаємо мінімум функціонала $T$ від функції $y=y(x)$, графіком якої є наша крива спуску:

$(13)T=T(y)=\underset{0}{\overset{x_B}{\int }}\sqrt{\frac{1+y{\text{'}}^2}{y}}dx$

Знаходження розв'язку

В точці локального мінімуму функціонала перша варіація функціонала $\delta T$ повинна дорівнювати нулю, а друга варіація ${\delta }^{2}T$ має бути більшою нуля (додатньо визначеною квадратичною формою від варіації аргументної функції $\delta y=\delta y(x)$).

З рівності нулю першої варіації слідує рівняння Ейлера — Лагранжа для функціонала (13):

$(14)\frac{d}{dx}{L}_{y^{\prime }}-L_y=0$

де лагранжиан $L$ дорівнює функції під інтегралом в (13):

$(15)L=L(y,y^{\prime })=\sqrt{\frac{1+y{\text{'}}^2}{y}},L_{y^{\prime }}=\frac{y^{\prime }}{\sqrt{y(1+y{\text{'}}^2)}},L_y=-\frac{\sqrt{1+y{\text{'}}^2}}{2y^{\begin{array}{c}\frac{3}{2}\end{array}}}$

З формул (14), (15) ми одержуємо звичайне диференціальне рівняння відносно невідомої функції $y=y(x)$:

$(16)\frac{d}{dx}\left(\frac{y^{\prime }}{\sqrt{y(1+y{\text{'}}^2)}}\right)+\frac{\sqrt{1+y{\text{'}}^2}}{2y^{\begin{array}{c}\frac{3}{2}\end{array}}}=0$

Але перше ніж розв'язувати (16), поглянемо на пошуки кривої з дещо іншої точки зору. А саме, припустимо, що наша крива спуску задана параметрично:

$(17)x=x(\tau ),y=y(\tau );\tau \in [{\tau }_A,{\tau }_B]$

параметр $\tau$ монотонно зростає при переміщенні вздовж нашої кривої, тобто є деякою досить довільною, але монотонно зростаючою функцією часу:

$(18)\tau =\tau (t),\frac{d\tau }{dt}>0$

Позначаючи крапкою зверху похідну функцій (17) по параметру $\tau$, ми можемо переписати функціонал (13) так:

$(19)T=\underset{{\tau }_A}{\overset{{\tau }_B}{\int }}\frac{\sqrt{{\dot{x}}^2+{\dot{y}}^2}}{\sqrt{y}}d\tau$

Очевидно, що величина інтеграла (19) не зміниться при заміні параметра $\tau$ на будь-яку іншу зростаючу функцію часу $\tilde{\tau }$:

$(20)\frac{d\tilde{\tau }}{dt}>0,\frac{d\tilde{\tau }}{d\tau }>0,\sqrt{{\dot{x}}^2+{\dot{y}}^2}d\tau =\sqrt{{\left(\frac{dx}{d\tilde{\tau }}\right)}^2+{\left(\frac{dy}{d\tilde{\tau }}\right)}^2}d\tilde{\tau }$

Для функціонала (19) ми матимемо два рівняння Ейлера-Лагранжа, $\tilde{L}=\tilde{L}(x,y,\dot{x},\dot{y})$:

$(21)\frac{d}{d\tau }{\tilde{L}}_{\dot{x}}-{\tilde{L}}_x=\frac{d}{d\tau }\left(\frac{\dot{x}}{\sqrt{y({\dot{x}}^2+{\dot{y}}^2)}}\right)=0$

$(22)\frac{d}{d\tau }{\tilde{L}}_{\dot{y}}-{\tilde{L}}_y=\frac{d}{d\tau }\left(\frac{\dot{y}}{\sqrt{y({\dot{x}}^2+{\dot{y}}^2)}}\right)+\frac{\sqrt{{\dot{x}}^2+{\dot{y}}^2}}{2y^{\begin{array}{c}\frac{3}{2}\end{array}}}=0$

Рівняння (21) і (22) так само, як і породивший їх інтеграл (19), інваріантні щодо заміни параметра $\tau$. Очевидно, що рівняння (22) переходить в (16) якщо взяти параметр кривої $\tau =x$. А от рівняння (21) виглядає простішим (зусилля витрачені на розгляд альтернативної точки зору виявилися не марними).

Починаємо розв'язувати звичайне диференціальне рівняння (21). Ми відразу можемо його проінтегрувати:

$(23)\frac{\dot{x}}{\sqrt{y({\dot{x}}^2+{\dot{y}}^2)}}=C=const$

Постійна інтегрування $C$ (однакова для всіх точок нашої шуканої кривої) має бути додатньою, оскільки ми обрали таку систему координат що кінцева точка В має більшу абсцису: $x_B>x_A=0$

Перепишемо (23) в іншому вигляді, виконавши алгебраїчні перетворення:

$(24){\dot{x}}^2(\frac{1}{C^2}-y)=y{\dot{y}}^2$

В правій частині останнього рівняння стоїть додатній вираз, а тому і вираз у дужках лівої частини повинен бути більшим нуля. Таким чином ордината нашої кривої лежить в межах:

$(25)0\le y\le \frac{1}{C^2}$

Оскільки параметр $\tau$ в формулі (24) довільний, зафіксуємо залежність ординати від параметра наступною функцією, враховуючи нерівності (25):

$(26)y=R(1-\cos \tau ),R=\frac{1}{2C^2}$

В початковій точці А кривої маємо $y_A=0$, а тому згідно з формулою (26) покладемо ${\tau }_A=0$

Будемо шукати залежність $x=x(\tau )$ таку, щоб задовольнити диференціальне рівняння (24):

$(27){\dot{x}}^2(2R-R(1-\cos \tau ))=R(1-\cos \tau )R^2{\sin }^2\tau$

Після алгебраїчних перетворень одержуємо:

$(27a){\dot{x}}^2(1+\cos \tau )=R^2(1-\cos \tau {)}^2(1+\cos \tau )$

$(27b)\dot{x}=R(1-\cos \tau )=y$

При переході з (27a) до (27b) ми врахували додатність константи інтегрування в формулі (23).

Формулу (27b) легко проінтегрувати, враховуючи початкову умову $x_A=x(0)=0$:

$(28)x(\tau )=\underset{0}{\overset{\tau }{\int }}\dot{x}d\tau =R(\tau -\sin \tau )$

Формули (26) і (28) є рівняннями циклоїди, заданої параметрично. Запишемо ще раз ці два рівняння окремо:

$(29)x=R(\tau -\sin \tau ),y=R(1-\cos \tau )$

Крива (29) є брахістохроною.

Узгодженість розв'язку

В ході розв'язування ми одержали три рівняння Ейлера-Лагранжа: (16), (21) і (22). Але розв'язок ми знайшли лише для рівняння (21). Покажемо, що знайдений розв'язок також задовольняє решту рівнянь (16) і (22).
Очевидно, що рівняння (16) можна одержати, поділивши (22) на $\dot{x}$. Тому нам достатньо перевірити, що розв'язок (29) задовольняє (22).
Спершу знайдемо суму квадратів похідних:

$(30){\dot{x}}^2+{\dot{y}}^2=R^2((1-\cos \tau {)}^2+{\sin }^2\tau )=2R^2(1-\cos \tau )=2Ry$

Підставляючи (30) і (29) в (22), знаходимо:

$(31)\frac{d}{d\tau }\left(\frac{\dot{y}}{\sqrt{y({\dot{x}}^2+{\dot{y}}^2)}}\right)+\frac{\sqrt{{\dot{x}}^2+{\dot{y}}^2}}{2y^{\begin{array}{c}\frac{3}{2}\end{array}}}=\frac{d}{d\tau }\left(\frac{\dot{y}}{\sqrt{2R}y}\right)+\frac{\sqrt{2R}}{2y}=$

$=\frac{1}{\sqrt{2R}}(\frac{d}{d\tau }\left(\frac{\sin \tau }{1-\cos \tau }\right)+\frac{1}{1-\cos \tau })=\frac{1}{\sqrt{2R}}(\frac{d}{d\tau }\mathrm{ctg}\frac{\tau }{2}+\frac{1}{2{\sin }^2\frac{\tau }{2}})=0$

Додатність другої варіації

Попередні обчислення

Запишемо інтеграл другої варіації функціонала (13):

$(32){\delta }^{2}T=\underset{0}{\overset{x_B}{\int }}(L_{yy}(\delta y{)}^2+2L_{y{y}^{\prime }}\delta y\delta y^{\prime }+L_{y^{\prime }{y}^{\prime }}(\delta y^{\prime }{)}^2)dx$

Знайдемо коефіцієнти квадратичної форми, враховуючи (15):

$(33)L_{yy}=\frac{3\sqrt{1+y{\text{'}}^2}}{4y^{\begin{array}{c}\frac{5}{2}\end{array}}},L_{y{y}^{\prime }}=-\frac{y^{\prime }}{2y^{\begin{array}{c}\frac{3}{2}\end{array}}\sqrt{1+y{\text{'}}^2}},L_{y^{\prime }{y}^{\prime }}=\frac{1}{\sqrt{y}(1+y{\text{'}}^2{)}^{\begin{array}{c}\frac{3}{2}\end{array}}}$

Нас цікавить значення другої варіації функціонала тільки в точці мінімуму, тобто тільки для кривої, що є брахістохроною. Виразимо коефіцієнти (33) через параматр $\tau$ циклоїди, скориставшись (29). Спочатку обчислимо:

$(34)y=R(1-\cos \tau )=2R{\sin }^2\frac{\tau }{2},y^{\prime }=\frac{\dot{y}}{\dot{x}}=\frac{\sin \tau }{1-\cos \tau }=\mathrm{ctg}\frac{\tau }{2},\sqrt{1+y{\text{'}}^2}=\frac{1}{\sin \frac{\tau }{2}}$

Тепер підставимо (34) в формули (33):

$(35)L_{yy}=\frac{3}{4(2R{)}^{\begin{array}{c}\frac{5}{2}\end{array}}{\sin }^6\frac{\tau }{2}}$

$(36)L_{y{y}^{\prime }}=-\frac{\cos \frac{\tau }{2}}{2(2R{)}^{\begin{array}{c}\frac{3}{2}\end{array}}{\sin }^3\frac{\tau }{2}}$

$(37)L_{y^{\prime }{y}^{\prime }}=\frac{{\sin }^2\frac{\tau }{2}}{\sqrt{2R}}$

Перша невдала спроба

Перевіримо, чи буде підінтегральна функція в (32) додатньо визначеною квадратичною формою. Для цього треба (необхідно і достатньо по критерю Сільвестра), щоб головні мінори матриці квадратичної форми були додатні:

$(38)\left|\begin{array}{c}{L}_{yy}\end{array}\right|=L_{yy}>0$

$(39)\left|\begin{array}{cc}{L}_{yy}& L_{y{y}^{\prime }}\\ L_{y^{\prime }y}& L_{y^{\prime }{y}^{\prime }}\end{array}\right|=L_{yy}{L}_{y^{\prime }{y}^{\prime }}-L_{y{y}^{\prime }}^2>0$

Підстановка (35) в (38) дає правильну нерівність, але нерівність (39) не виконується з врахуванням формул (35-37):

$(40)L_{yy}{L}_{y^{\prime }{y}^{\prime }}-L_{y{y}^{\prime }}^2=\frac{1}{(2R{)}^3}\left(\frac{3{\sin }^2\frac{\tau }{2}-\cos \frac{\tau }{2}}{4{\sin }^6\frac{\tau }{2}}\right)$

Зокрема, на початку руху по брахістохроні параметр $\tau$ близький до нуля, косинус близький до одиниці, а тому вираз (40) від'ємний.

Друга спроба

Якби варіація $\delta y=\delta y(x)$ та її похідна $\delta y^{\prime }$ були незалежними і довільними функціями, то ми б дійсно могли підібрати ці функції так щоб в кожній точці $x$ підінтегральний вираз в (32) був від'ємним або нульовим, і таким чином весь інтеграл (32) міг би бути від'єним.

Але насправді між функцією та її похідною є зв'язок. Оскільки на кінцях нашої кривої варіація перетворюється в нуль

$(41)\delta y{|}_{x=0}=\delta y{|}_{x=x_B}=0$

то ми маємо тотожно:

$(42)0=L_{y{y}^{\prime }}(\delta y{)}^2{|}_0^{x_B}=\underset{0}{\overset{x_B}{\int }}\frac{d}{dx}(L_{y{y}^{\prime }}(\delta y{)}^2)dx=\underset{0}{\overset{x_B}{\int }}(\left(\frac{d}{dx}{L}_{y{y}^{\prime }}\right)(\delta y{)}^2+2L_{y{y}^{\prime }}\delta y\delta y^{\prime })dx$

Віднімемо від інтеграла другої варіації (32) тотожність (40), одержимо такий вираз для другої варіації:

$(43){\delta }^{2}T=\underset{0}{\overset{x_B}{\int }}((L_{yy}-\frac{d}{dx}{L}_{y{y}^{\prime }})(\delta y{)}^2+L_{y^{\prime }{y}^{\prime }}(\delta y^{\prime }{)}^2)dx$

Покажемо, що підінтегральний вираз в (43) буде додатнім на брахістохроні. Другий доданок буде додатнім внаслідок формули (37). Покажемо тепер, що додатньою буде також перший доданок, обчислимо різницю:

$(44)L_{yy}-\frac{d}{dx}{L}_{y{y}^{\prime }}=L_{yy}-\frac{1}{\dot{x}}\frac{d}{d\tau }{L}_{y{y}^{\prime }}=\frac{3}{4(2R{)}^{\begin{array}{c}\frac{5}{2}\end{array}}{\sin }^6\frac{\tau }{2}}-\frac{1}{2R{\sin }^2\frac{\tau }{2}}\frac{d}{d\tau }(-\frac{\cos \frac{\tau }{2}}{2(2R{)}^{\begin{array}{c}\frac{3}{2}\end{array}}{\sin }^3\frac{\tau }{2}})=$

$=\frac{1}{2(2R{)}^{\begin{array}{c}\frac{5}{2}\end{array}}{\sin }^2\frac{\tau }{2}}(\frac{3}{2{\sin }^4\frac{\tau }{2}}+\frac{d}{d\tau }\left(\frac{\cos \frac{\tau }{2}}{{\sin }^3\frac{\tau }{2}}\right))=\frac{1}{2(2R{)}^{\begin{array}{c}\frac{5}{2}\end{array}}{\sin }^2\frac{\tau }{2}}>0$

Отже друга варіація функціонала (13) додатня на брахістохроні, тобто брахістохрона є локальним мінімумом цього функціонала.

Джерела

• Шаблон:УРЕ