Функція Розенброка

Графік функції Розенброка для двох змінних. В даному прикладіі $a=1,b=100$, а мінімальне значення функції дорівнює нулю і досягається в координатах $(1,1)$.

Функція Розенброка у математичній оптимізації — неопукла функція, яка використовується для тестування продуктивності алгоритмів оптимізації. Була представлена Шаблон:Нп у 1960 році.

Глобальний мінімум функції знаходиться всередині довгої вузької плоскої фігури параболічної форми. Що робить складним пошук шлях до глобального мінімуму для алгоритмів оптимізації.

Функція визначається як:

$f(x,y)=(a-x{)}^2+b(y-x^2{)}^2$

Функція має глобальний мінімум при $(x,y)=(a,a^2)$, де $f(x,y)=0$. Зазвичай ці параметри встановлюються так, що $a=1$ і $b=100$. Але тільки в тривіальному випадку, де $a=0$, функція симетрична, а мінімум знаходиться в початку координат.

Багатовимірні узагальнення

Зазвичай зустрічаються два варіанти.

Анімація функції Розенброка трьох змінних

Ця багатовимірна функція є сумою $N/2$ незв'язаних 2D функцій Розенброка, і визначається лише для парних $N$:

$f(𝐱)=f(x_1,x_2,\dots ,x_N)=\sum _{i=1}^{N/2}[100(x_{2i-1}^2-x_{2i}{)}^2+(x_{2i-1}-1{)}^2].$

Цей варіант має передбачувано прості рішення.

Другий, більш складний варіант:

$f(𝐱)=\sum _{i=1}^{N-1}[100(x_{i+1}-x_i^2{)}^2+(1-x_i{)}^2],\text{де}𝐱=(x_1,\dots ,x_N)\in {ℝ}^N.$

має рівно один мінімум для $N=3$ (при $(1,1,1)$) і рівно два мінімуми для $4\le N\le 7$ — глобальний мінімум при $(1,1,...,1)$ і локальний мінімум поблизу $\widehat{𝐱}=(-1,1,\dots ,1)$. Цей результат отримано шляхом встановлення градієнта функції рівним нулю, зауваживши, що отримане рівняння є раціональною функцією $x$. Для маленьких $N$ поліноми можна визначити точно, а теорему Штурма можна використати для визначення кількості справжніх коренів, тоді як корені можуть бути обмежені в області $|x_i|<2.4$. Для більшого $N$ цей метод не працює через велике значення задіяних коефіцієнтів.

Стаціонарні точки

Багато стаціонарних точок функції демонструють правильну закономірність під час побудови. Цю структуру можна використати, щоб знайти їх.

Графіки розв'язання цієї функції мають горбисті структури

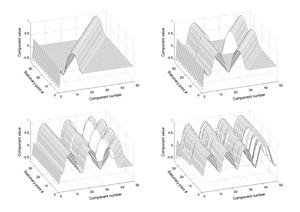
Приклади оптимізації

Метод Нелдера-Міда, застосований до функції Розенброка

Функцію Розенброка можна ефективно оптимізувати шляхом адаптації відповідної системи координат без використання будь-якої інформації про градієнт і без побудови локальних апроксимаційних моделей (на відміну від багатьох оптимізаторів без похідних). Наступний малюнок ілюструє приклад двовимірної оптимізації функції Розенброка за допомогою адаптивного спуску координат від початкової точки $x_0=(-3,-4)$. Розв'язок зі значенням функції $10^{-10}$ можна знайти після 325 оцінок функцій.

Використання методу Нелдера–Міда з початкової точки $x_0=(-1,1)$ з регулярним початковим симплексом. Мінімум знайдено зі значенням функції $1.36\cdot 10^{-10}$ після 185 оцінок функцій. Шаблон:Clear

Див. також

• Тестові функції для оптимізації

Посилання

• Тривимірний графік функції Розенброка
• Шаблон:MathWorld