Букет просторів

Букет просторів — топологічний простір, який інтуїтивно можна отримати склеюванням декількох топологічних просторів по одній точці в кожному просторі. Букети просторів часто використовуються в алгебричній топології для обчислень фундаментальних груп і груп гомологій.

Означення

Букет $X_1\vee X_2$ двох просторів $X_1$ і $X_2$ із виділеними точками $x_1\in X_1$ і $x_2\in X_2$ можна визначити як фактор-простір диз'юнктного об'єднання $X_1$ і $X_2$

$X_1\vee X_2=(X_1⨿X_2)/\sim ,$

де $\sim$ позначає мінімальне відношення еквівалентності таке, що $x_1\sim x_2$. У цьому відношенні всі класи еквівалентності складаються з однієї точки за винятком одного, до якого належать дві точки $x_1,x_2$.

Подібним чином визначається букет довільної множини просторів із виділеними точками $\{(X_{\alpha },x_{\alpha }){\}}_{\alpha \in 𝒜}$

$\underset{\alpha }{\bigvee }{X}_{\alpha }=\coprod _{\alpha }{X}_{\alpha }/\sim ,$

де $\sim$ позначає мінімальне відношення еквівалентності таке, що $x_{\alpha }\sim x_{\beta }$ для всіх $\alpha$ і $\beta$. Як і вище, для цього відношення всі класи еквівалентності складаються з однієї точки за винятком одного, до якого належать всі виділені точки $x_{\alpha }$.

Букет загалом залежить від вибору виділених точок і природним чином є простором з виділеною точкою.

Опис через категорії

Букет можна розуміти як кодобуток в категорії топологічних просторів з виділеною точкою. Крім того, букет можна розглядати як кодекартів квадрат схеми X < {•} > Y в категорії топологічних просторів, де {•} позначає простір з однієї точки.

Приклади

Букет двох кіл з виділеними точками

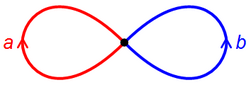
• Букет двох кіл з виділеними точками є гомеоморфним «вісімці» (див. рисунок).
• Букет з двох сфер (розмірності 2) зображений на нижньому рисунку.
• В теорії гомотопій важливою конструкцією є ідентифікація точок, що лежать на деякому екваторі n-сфери $S^n$. Отриманий при цьому простір є букетом двох сфер $S^n$:

$S^n/\sim =S^n\vee S^n$

Властивості

• Як бінарна операція, побудова букета є асоціативною і комутативною (з точністю до ізоморфізму).
• Якщо відмічені точки допускають однозв'язні околи, то фундаментальна група букета $X_1\vee X_2$ ізоморфна вільному добутку фундаментальних груп $X_1$ і $X_2$. Це твердження випливає з теореми Зейферта — ван Кампена.
• Нехай X є букетом двох просторів K і L з виділеними точками p і q і до того ж виділені точки є деформаційними ретрактами для деяких своїх околів U ⊂ K і V ⊂ L. Остання властивість означає, що наприклад відображення ${\mathrm{Id}}_U:{\mathrm{Id}}_U(x)=x,\mathrm{\forall }x\in U$ є гомотоптим сталому відображенню, що для всіх елементів U приймає значення p і подібно для L і q. При цих припущеннях справедливою є рівність для редукованих гомологічних груп:

${\tilde{H}}_n(K\vee L)\cong {\tilde{H}}_n(K)\oplus {\tilde{H}}_n(L).$

Зокрема для прикладів розглянутих вище:

${\tilde{H}}_n(S^1\vee S^1)\cong \{\begin{array}{cc}\mathbb{Z}\oplus \mathbb{Z}& n=1\\ 0& \text{if }n\ne 1\end{array}$

${\tilde{H}}_n(S^2\vee S^2)\cong =\{\begin{array}{cc}\mathbb{Z}\oplus \mathbb{Z}& n=2\\ 0& \text{if }n\ne 2\end{array}$

• Подібне співвідношення є справедливим і для відносних гомологічних груп:

$H_n(K\vee L,p=q)\cong H_n(K,p)\oplus H_n(L,q).$

Див. також

• Смеш-добуток

Література

• Шаблон:Cite book
• Шаблон:Citation