Ефект Саньяка

Ефект Саньяка (інтерференція Саньяка), названий на честь французького фізика Жоржа Саньяка, — явище інтерференції, яке виникає внаслідок обертання. Як правило, це явище проявляє себе в кільцевій інтерферометрії. Світловий промінь розбивається на два, що прямують у протилежних напрямах по замкненому кільцю. Очевидно, що кільце має певну площу і тому розміри інтерференційної картини (ширина смуги) залежать від цієї площі. Положення інтерференційних смуг залежить від частоти обертання установки. Подібне обладнання також називається інтерферометром Саньяка.

Ефект Саньяка — електромагнітний двійник механічного обертання. Вектор кутової швидкості

$\mathit{\omega }=\frac{1}{2}[\mathrm{\nabla }\times 𝐯]$

аналогічний аксіальному вектору індукції магнітного поля, а вектор швидкості

$𝐯=[\mathit{\omega }\times 𝐫]$

аналогічний векторному потенціалу.

Підвіс карданів гіроскопа залишається після закрутки в одному й тому ж стані (напрямі), і тому може бути використаний як референтна система відліку. Інтерферометр Саньяка може вимірювати свою власну кутову частоту відносно локальної системи відліку.

Схематичне зображення інтерферометра Саньяка

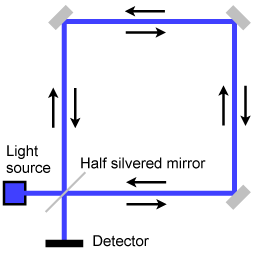
Опис явища

Як правило, використовують декілька дзеркал, так що промінь світла описує трикутну або чотирикутну траєкторію. Для колової схеми можна використати фіберволокно, яке досить пластичне і може бути зігнуте в коло. Кільцевий інтерферометр розміщується на платформі, що може обертатися навколо своєї осі. Коли платформа обертається, то інтерференційні смуги зміщуються відносно нерухомого стану. Величина зсуву пропорційна кутовій швидкості платформи. Вісь обертання не обов'язково повинна міститися всередині замкнутої площі кільця.

Коли платформа обертається, то точка входу/виходу також рухається з транзитним часом, прив'язаним до руху світла. Тому один промінь пройде меншу відстань, ніж другий. Це і спричиняє зсув інтерференційних смуг. Таким чином, інтерференційна картина буде залежати від кутової швидкості обертання платформи з різними значеннями відносного фазового зсуву.

Історія

Уперше теоретично ефект передбачив Олівер Лодж у 1897 році, а потім Альберт Майкельсон у 1904 році. Вони сподівались, що в свій час хтось зможе здійснити грандіозний експеримент із вимірювання кутової швидкості обертання Землі навколо своєї осі за допомогою оптичних засобів інтерферометрії. Більш того, вони припускали, що у випадку коли Земля (або інтерферометр) захоплює «світлоносний ефір», то результат буде «негативним», проте у випадку «стаціонарного ефіру» — результат буде «позитивним». Макс фон Лауе в 1911 році продовжив теоретичну роботу Майкельсона, і використав у своїх розрахунках спеціальну теорію відносності. Він передбачив (із точністю до першого порядку відносно v/c) однакове значення відносного зсуву фази для випадку «стаціонарного ефіру» та релятивістського підходу, оскільки в обох випадках швидкість світла є незалежною від швидкості джерела світла, і тому поширення протилежно направлених променів описується однаково з точки зору інерційної системи відліку. Тому тільки модель тотального захоплення ефіру дасть «негативний» результат.

На практиці цю інтерференційну схему вперше реалізував французький фізик Жорж Саньяк у 1913 році і тому це явище названо на його честь. Його мета полягала в детектуванні «ефекту відносного руху ефіру» Саньяк тільки згадав сумісність результатів зі «стаціонарним ефіром». Проте, як уже згадано вище Макс фон Лауе вже передбачив цей ефект за допомогою релятивістського підходу і тому цей ефект також сумісний з релятивістським підходом.

У 1925 році амбітний експеримент із кільцевої інтерферометрії здійснили Альберт Майкельсон та Генрі Гейл. Основною метою експерименту було з'ясувати, чи обертання Землі впливає на поширення світла біля Землі. Експеримент Майкельсона — Гейла являв собою «гігантський кільцевий інтерферометр» з периметром близько 1,9 км. Площі кільця було достатньо для вимірювання кутової швидкості Землі. В результаті цього експерименту підтверджено, що кутова швидкість обертання Землі, виміряна в рамках астрономії, збігається з інтерферометричною швидкістю. Калібрування основного кільцевого інтерферометра здійснювалася за допомогою додаткового інтерферометра, розміри якого в широтному напрямі були значно меншими, ніж у основного інтерферометра. Оскільки оптичні осі обох інтерферометрів збігалися, то можна було досить легко за допомогою додаткової процедури настроювати основний інтерферометр на спільну оптичну вісь, відносно якої і вимірювався зсув смуги. Середнє значення відносного зсуву фази було 0,230, тоді як теоретична модель передбачала близьке значення 0,237.

Теоретичні пояснення

Після відкриття ефекту Саньяка пройшло більше 100 років, проте донині відсутнє чітке розуміння цього явища. Оскільки в його основі лежать інтерференційні явища, які в свою чергу можуть викликатися не тільки хвилями, але й елементарними частками, то на сьогодні існують десятки моделей, які «коректно», або «не зовсім» (у термінології Маликіна) описують його фізичну природу. В історичному плані одне з перших пояснень, яке ґрунтується на концепції стаціонарного ефіру, належить самому Саньяку.

Модель «стаціонарного ефіру»

Зсув інтерференційних смуг можна розглядати як простий результат різниці шляхів поширення двох променів світла, обумовлений обертанням платформи. Найпростіше виведення ґрунтується на круглому кільці, що обертається з кутовою швидкістю $\omega$, проте отриманий результат можна поширити й на інші форми шляху. Якщо джерело світла випромінює у двох протилежних напрямах кільця, що обертається, тоді світло в напрямі обертання пройде більший шлях, ніж світло в протилежному напрямі, і досягне джерела в момент часу $t_1$:

Світло поширюється у протилежних напрямах і проходить різні шляхи, повертаючись знову до джерела.

$t_1=\frac{2\pi R+\mathrm{\Delta }L}{c}$

де $\mathrm{\Delta }L$ — різниця шляхів двох променів (чорна жирна стрілка на фігурі):

$\mathrm{\Delta }L=R\omega t_1.$

Виключивши з обох рівнянь $\mathrm{\Delta }L$ можна отримати:

$t_1=\frac{2\pi R}{c-R\omega }.$

Подібно можна отримати час проходження другого променя, який прямує назустріч обертанню платформи:

$t_2=\frac{2\pi R}{c+R\omega }.$

Тоді різниця часу буде:

$\mathrm{\Delta }t=t_1-t_2=\frac{4\pi R^2\omega }{c^2-R^2{\omega }^2}.$

Оскільки $R\omega =v\ll c$, то можна спростити цеий вираз до

$\mathrm{\Delta }t\approx \frac{4\pi R^2\omega }{c^2}=\frac{4A\omega }{c^2},$

де A — площа кільця, в якому поширюється світло. Цей результат можна поширити на будь-яку форму замкненого шляху, сумарна площа якого A.

Для спостереження інтерференційної картини можна використати уявний екран, а можна використати роздільник світла і направити результат на матеріальний екран. Якщо світло має форму імпульсів, коротших за $\mathrm{\Delta }t$, то інтерференційної картини не буде. Проте в експериментах використовують стаціонарні джерела світла (зокрема й неперервні лазери) і тому спостерігається стабільна інтерференційна картина. Фазовий зсув має вигляд $\mathrm{\Delta }\varphi =\frac{2\pi c\mathrm{\Delta }t}{\lambda }$, що викликає зсув інтерференційної смуги пропорційно площі $A$ та кутовій швидкості $\omega$.

У випадку поширення світла у вакуумі дорелятивістські та релятивістські моделі дають однаковий результат. Іншими словами, у випадку вакуумного ефекту Саньяка експеримент не розрізняє між дорелятивістською та релятивістською фізиками.

Модель «часткового захоплення ефіру»

У випадку матеріального середовища (матеріального носія) з певним показником заломлення ефект Саньяка можна розглянути зі врахуванням коефіцієнту захоплення Френеля. В цьому випадку швидкості променів уздовж обортання і навпаки можна подати у вигляді:

$v_f^{\pm }=\frac{c}{n}\pm (1-f)R\omega$,

де $f=1-1/n^2$ — коефіцієнт захоплення Френеля. Тоді результуючі швидкості можна переписати у вигляді:

$v_f^{\pm }=\frac{c}{n}\pm \frac{R\omega }{n^2}$.

Час, який витрачають два промені світла для обходу кільця буде:

$t^{\pm }=\frac{2\pi R}{c/n\mp R\omega /n^2}$.

Різниця часу проходження двох променів кільцем буде:

$\mathrm{\Delta }t=t^{+}-t^{-}=\frac{4\pi R^2\omega }{c^2(1-R^2{\omega }^2/c^2{n}^2)}$.

Враховуючи очевидне співвідношення $R^2{\omega }^2\ll c^2{n}^2$, цей вираз можна переписати:

$\mathrm{\Delta }t\approx \frac{4\pi R^2\omega }{c^2}$,

звідки видно, що результат не залежить від показника заломлення для конкретного середовища (носія).

Релятивістська модель

Першим, хто спробував пояснити ефект Саньяка в рамках релятивістського підходу був Шаблон:Нп. Оскільки цей ефект не є результатом штучного вибору системи відліку, то він також не залежить від її вибору. Зільберштейн використав метрику Мінковського і зробив перетворення координат $x=r\cos (\theta +\omega t)$ та $y=r\sin (\theta +\omega t)$, тоді лінійний елемент метрики буде:

$d{s}^2=(c^2-r^2{\omega }^2)d{t}^2-d{r}^2-r^{2}d{\theta }^2-d{z}^2-2r^2\omega dtd\theta$

де

• $t$ — істинний час для спостерігача,
• $r$ — відстань від центра,
• $\theta$ — кутова відстань вздовж кільця в напрямі спостерігача,
• $z$ — напрям, перпендикулярний до площі кільця,
• $\omega$ — швидкість обертання кільця та спостерігача.

В рамках цієї метрики швидкість світла дотична до кільця $c\pm r\omega$ і залежить від напряму поширення світла вздовж кільця. Слід відзначити, що тільки у випадку $\omega =0$ ми маємо «інерційну систему». Проте у випадку $\omega \ne 0$ ми маємо «неінерційну систему». Тому в точці спостерігача (при $r=0$) маємо відмінні від $c$ значення швидкості світла, які змінюються в залежності від напряму їх приходу.

Проте цей підхід не сподобався Зільберштейну і надалі він звернувся до загальної теорії відносності. Детальніше цю проблему висвітлено у праці Маликіна. Безумовно Зільберштейн знав думку Ейнштейна з цього приводу: Шаблон:Quotation

Що зробив Макс фон Лауе?

Традиційно вважають, що Макс фон Лауе продовжив розгляд роботи Майкельсона на основі теорії відносності. Чи так це? Насправді Макс фон Лауе в кінці своєї статі написав: Шаблон:Quotation

Ніяких посилань на спеціальну теорію відносності у формі Лоренца, чи Ейнштейна в статті Лауе немає. Проте є варте уваги посилання на Шаблон:Нп, фахівця з електродинаміки.

Електродинаміка Кона

Питання, яке випливає зі статті Майкельсона, має відповідь у рамках електродинамічного підходу Кона. Коротко, його положення такі: якщо уявити площину експеримента в довільній точці на Землі тангенціонально до неї, то часове зміщення dt, необхідне світлу для проходження відстані ds (вимірюване на Землі) можна подати у формі $\frac{{𝔮}_{s}ds}{c^2}$, якщо ds рухається зі швидкістю $𝔮$. Тому поширення світла для додатного напряму обертання буде $\frac{1}{c^2}\underset{0}{\int }{𝔮}_{s}ds$ довше ніж у протилежному випадку, а тому буде меншим для від'ємного обертання променя в даній точці. Якщо ми використаємо для лінійного інтегралу теорему Стокса, то можна знайти

$\mathrm{\Delta }\tau =r_{+}-r_{-}=\frac{2}{c^2}\underset{0}{\int }{𝔮}_{s}ds=\frac{2}{c^2}F{𝗋𝗈𝗍}_n𝔮$

Проте, якщо Ω - кутова швидкість обертання Землі, то

$\left|\mathrm{r}\mathrm{o}\mathrm{t}𝔮\right|=2\mathrm{\Omega },$

де φ — широта проведення експерименту,

${𝗋𝗈𝗍}_n𝔮=2\mathrm{\Omega }\sin \phi$

і, відповідно до формули (6), буде:

$\mathrm{\Delta }\tau =\frac{4}{c^2}\mathrm{\Omega }F\sin \phi .$

Може здатися сумнівним, звичайно, чи допустимо використовувати лінійний інтеграл за об'ємом? оскільки промені, по відношенню до площі, що обертається, не можуть поширюватися по прямих лініях. Проте детальний розгляд цих обставин, дасть тільки корекцію більш високого порядку відносно Δτ.

Таким чиним, із того факту, що Макс фон Лауе заперечував підхід Генріха Герца, зовсім не випливає, що він першим описав ефект Саньяка з позицій спеціальної теорії відносності. Більш того, Макс фон Лауе за замовчуванням не може бути т.з. «передвісником» ефекту Саньяка, оскільки він тривіально модернізував «теорію стаціонарного ефіру Майкельсона». Іншими словами, саме Альберт Майкельсон і є справжнім автором т. з. «ефекту Саньяка».

Квантова природа ефекту Саньяка

Квантова природа ефекту Саньяка ґрунтується на підході Майкельсона (1904), котрий уперше почав розглядати циркуляцію вектора за замкнутим контуром. Звичайно, Майкельсон не знав квантової механіки, котрої на той час ще не було, проте він був прихильником «медіафізики Гельмгольца» і тому цілком розумів природу «вортексів», котрі в потенції містили в собі майбутнє квантове подання. Відомо, що квантування циркуляції швидкості відкрив Фейнман тільки всередині 1950-х років, тому квантові підходи до розуміння ефекту Саньяка з'явились тільки на кінець XX століття. В рамках стандартної фізики ці підходи називають «методами аналогій», і розцінюють, на відміну «ефіроносних підходів», більш м'яко, як «попутники» релятивістського підходу. Одні дослідники розглядають, як варіант фази Беррі, а інші — як аналог ефекта Ааронова — Бома.

У загальному випадку циркуляцію швидкості можна записати у вигляді:

${\mathrm{\Phi }}_v={\oint }_L𝐯,d𝐥=\underset{S}{\iint }rot𝐯,d𝐬=2\underset{S}{\iint }\omega ,d𝐬$.

Квант циркуляції швидкості записується у формі Фейнмана:

${\mathrm{\Phi }}_v(n)=2\underset{S_q}{\iint }\omega ,d𝐬=\frac{h}{m_v}n={\mathrm{\Phi }}_{n0}n$,

де $n=integer$, ${\mathrm{\Phi }}_{n0}=h/m_v$ — квант циркуляції швидкості, або вортекс/вихор, $h$ — стала Планка, а $m_v$ — «вортексна маса». Відносний фазовий зсув можна визначити як відношення циркуляцій швидкості:

${\xi }_v=\frac{{\mathrm{\Phi }}_v}{{\mathrm{\Phi }}_{v0}}=\frac{2m_v}{h}\underset{S}{\iint }\omega ,d𝐬=\frac{2m_v}{h}(\mathit{\omega }\cdot 𝐬)$.

У випадку, коли вортексна маса рівна двом масам фотона світла

$m_v=2m_{\lambda }=2\frac{h}{c\lambda }$

можна отримати загальний вираз для відносного зсуву фази у вигляді:

${\xi }_v=\frac{4}{c\lambda }(\mathit{\omega }\cdot 𝐬)=\frac{c}{\lambda }\mathrm{\Delta }t$,

де

$\mathrm{\Delta }t=4(\mathit{\omega }\cdot 𝐬)/c^2$

є різниця часу для квантового ефекту Саньяка.

Медіафізика вихорів Гельмгольца

В 1858 році Гельмгольц не тільки визначив кінематично вортексний/вихровий рух, проте він також в основному довів до кінця і свою динамічну теорію. Основний зміст цієї теорії полягає в законі збереження: вихори не можуть виникати а також не можуть зникати. Або в загальнішій формі — інтенсивність вихору постійна в часі. Томсон спростив підхід Гельмгольца, використавши математичне поняття циркуляції (тоді ще не було визначення векторів!). Таким чином, в рамках підходу Гельмгольца — Томсона циркуляція швидкості за замкнутим контуром є величина:

${\mathrm{\Phi }}_v={\oint }_L𝐯,d𝐥$.

В сучасних термінах теорему про збереження вортексу Гельмгольца можна сформулювати так: Шаблон:Quotation

$\frac{d{\mathrm{\Phi }}_v}{dt}=0$, ${\mathrm{\Phi }}_v=const.$

Один із наслідків теореми полягає в тому, що для кільцевого вортексу, який наближається до плоскої стінки, його розміри збільшуються (див. мал.32). В граничному випадку, коли стінка має нескінченні розміри, тоді вортекс може «зникнути» (буде поглинутий стінкою). Дане твердження не суперечить теоремі Гельмгольца, оскільки одностороннє обмеження простору з довільного боку неможливе в природі. Екрани або стінки завжди мають обмежені розміри і тому наближення вихору до них тільки збільшує їх розміри.

Див. також

• Експеримент Майкельсона — Гейла
• Корпускулярно-хвильовий дуалізм
• Волоконно-оптичний гіроскоп

Посилання

• Large Laser Gyroscopes for Monitoring Earth Rotation Шаблон:Webarchive
• Mathpages article on the Sagnac Effect
• Ring-laser tests of fundamental physics and geophysics (Extensive review by G E Stedman. PDF-file, 1.5 MB)
• The Sagnac Effect and its Application for GPS GPS-related article by Neil Ashby
• Live data from New Zealand 21 m x 40 m ring laser gyro