Лемніската Бернуллі

Лемніската і її фокуси

Шаблон:UniboxЛемніската Бернуллі (Шаблон:Lang-el — пов'язка) — плоска алгебрична крива, яку можна означити як геометричне місце точок $P$, для кожної з яких добуток відстаней до двох заданих точок $F_1$ та $F_2$ (фокусів) незмінна і дорівнює квадрату половини відстані між фокусами.

Тобто, для кожної точки $P$ лемніскати виконується рівність:

$P{F}_1\cdot P{F}_2=c^2$.

де $2c$ — відстань між фокусами $F_1{F}_2$.

Назва походить з античного Риму, де «лемніскатою» називали бантик, з допомогою якого прикріпляли вінок до голови переможця на спортивних іграх. Цю лемніскату називають в честь швейцарського математика Якоба Бернуллі, який поклав початок її вивченню в 1694 році.

Лемніската Бернуллі — алгебрична крива 4 порядку. Є окремим випадком овалів Кассіні та синусоїдальних спіралей.

Рівняння

Нехай фокуси лемніскати Бернуллі знаходяться на осі $Ox$ в точках $F_1(-c;0)$ і $F_2(c;0)$. Відстань між фокусами дорівнює $2c$, а точка $O$ — початок координат ділить відрізок між фокусами навпіл. Тоді наступні рівняння задають лемніскату Бернуллі:

• в прямокутних координатах в неявному виді:

$(x^2+y^2{)}^2=2c^2(x^2-y^2)$

Зробивши нескладні перетворення, можна отримати рівняння у явному вигляді:

$y=\pm \sqrt{\sqrt{c^4+4x^2{c}^2}-x^2-c^2}$

• в полярних координатах:

${\rho }^2=2c^2\cos 2\phi .$

Крива визначена при $\phi \in [0,\frac{\pi }{4}]\cup [\frac{3\pi }{4},\frac{5\pi }{4}]\cup [\frac{7\pi }{4},2\pi ]$ ;

або ж при $\phi \in [-\frac{\pi }{4},\frac{\pi }{4}]\cup [\frac{3\pi }{4},\frac{5\pi }{4}]$

• Параметричне рівняння в прямокутній декартовій системі координат:

$\{\begin{array}{c}x=c\sqrt{2}\frac{p+p^3}{1+p^4}\\ y=c\sqrt{2}\frac{p-p^3}{1+p^4}\end{array}$, де $p^2=\mathrm{tg}(\frac{\pi }{4}-\phi )$

Щоб задати лемніскату по двох довільних точках, можна не виводити рівняння заново, а визначити перетворення координат, при якому старий (даний) фокусний відрізок переходить в новий, і подіяти на представлені рівняння цим перетворенням.

• Шаблон:Не перекладено для лемніскати Бернуллі має вигляд:Шаблон:Sfn Шаблон:Rp Шаблон:Sfn Шаблон:Rp

$\ell =3\cdot \int \frac{dR}{\sqrt{{(\frac{3}{c}\cdot R)}^4-1}}$

де
$\rho$ — радіус кривини лемніскати Бернуллі в певній точці;
$\ell$ — довжина дуги лемніскати від її початку до цієї точки.

Властивості та особливості форми

Лемніската, вписана в коло

• Для довільної точки $P$ лемніскати Бернуллі з фокусами $F_1$ та $F_2$ справедливе наступне твердження (альтернативне означення лемніскати):

$\mathrm{|}\mathrm{P}{\mathrm{F}}_{\mathrm{1}}\mathrm{-}\mathrm{P}{\mathrm{F}}_{\mathrm{2}}\mathrm{|}\mathrm{=}\mathrm{O}\mathrm{P}\sqrt{\mathrm{2}}\mathrm{.}$

де $O$ — середина відрізка $F_1{F}_2$. Шаблон:Hider

• Лемніската — алгебрична крива четвертого порядку.
• Вона має дві осі симетрії: пряма, на якій лежить $F_1{F}_2$, і серединний перпендикуляр цього відрізка; для розглянутого випадку — вісь $Oy$.
• Точка, де лемніската перетинає саму себе, називається вузловою чи подвійною точкою.

Для розглянутого випадку подвійною точкою лемніскати є початок координат.

• Дотичні в подвійній точці лемніскати — прямі $y=\pm x$, складають з відрізком $F_1{F}_2$ кути $\pm \frac{\pi }{4}$ і є взаємно перпендикулярними. Шаблон:Sfn Шаблон:Rp
• Кут $\mu$ між дотичною до лемніскати в її довільній точці радіус-вектором точки дотику дорівнює: Шаблон:Sfn Шаблон:Rp

$\mu =2\phi +\frac{\pi }{2}$.

• Дотичні до лемніскати, які проведені на кінцях хорди, що проходить через її подвійну точку, паралельні між собою.
• Кут між перпендикуляром, проведеним до дотичної із початку координат, та полярною віссю втричі більший за полярний кут $\phi$ точки дотику. Таким чином, лемніскату можна використовувати для трисекції кута.Шаблон:Sfn Шаблон:Rp

• Лемніската Бернуллі перетинає вісь $Ox$ в точках

$A(c\cdot \sqrt{2};0)$ та $B(-c\cdot \sqrt{2};0)$.

• Крива має 2 максимуми і 2 мінімуми. Їх координати:

  $\{\begin{array}{c}x=\pm \frac{\sqrt{3}}{2}c\\ y=\pm \frac{c}{2}\end{array}$

• Відстань від максимуму до мінімуму, що знаходяться по одну сторону від серединного перпендикуляра (осі $Oy$ в даному випадку) дорівнює відстані від максимуму (чи від мінімуму) до подвійної точки.

• Інверсія лемніскати ${\rho }^2=2c^2\cos 2\phi .$ з центром в подвійній точці, переводить леминіскату Бернуллі в синусоїдальну спіраль ${\rho }^{-2}=2c^2\cos 2\phi .$, тобто в рівнобічну гіперболу.Шаблон:Sfn Шаблон:Rp
• Подерою лемніскати Бернуллі є cинусоїдальна спіраль

${\rho }^{\frac{2}{3}}=(\sqrt{2}c{)}^{\frac{2}{3}}\cos \left(\frac{2}{3}\phi \right)$

Лемніската в свою чергу є подерою рівнобічної гіперболи.

• Лемніската є геометричним місцем точок, що симетричні з центром рівнобічної гіперболи, по відношенню до її дотичних. Шаблон:Sfn Шаблон:Rp
• Кінематично лемніскату можна отримати як траекторію середини великої ланки шарнірного антипаралелограма, протилежна ланка якого нерухомо закріплена.Шаблон:Sfn Шаблон:Rp
• Відрізок бісектриси кута між фокальними радіусами-векторами точки лемніскати дорівнює відрізку від центру лемніскати до перетину її осі з цією бісектрисою. Шаблон:Sfn Шаблон:Rp
• Геометричне місце проєкцій центрів кривини лемніскати на відповідні радіуси-вектори є також лемніската, рівняння якої:

${\rho }^2=\frac{4}{9}{c}^2\cos 2\phi .$

Метричні характеристики

Нехай лемніската Бернуллі задана рівнянням в полярній сисемі координат: ${\rho }^2=2c^2\cos 2\phi$. Тоді:

• Довжина дуги лемніскати між точками, що відповідають полярним кутам $0\le \phi \le {\phi }_1$:

$\ell =c\cdot \underset{0}{\overset{{\phi }_1}{\int }}\frac{d\phi }{\sqrt{1-2{\sin }^2\phi }}$

Виконавши заміну $2{\sin }^2\phi ={\sin }^2\theta$, приводимо інтеграл до виду:

$\ell =\frac{c}{\sqrt{2}}\cdot \underset{0}{\overset{{\theta }_1}{\int }}\frac{d\theta }{\sqrt{1-\frac{1}{2}{\sin }^2\theta }}=\frac{c}{\sqrt{2}}\cdot F(\frac{1}{\sqrt{2}},\theta )$

де $F(k,\theta )$ — неповний еліптичний інтеграл 1-го роду.

Довжина всієї лемніскати Бернуллі:

$\ell =4\cdot \frac{c}{\sqrt{2}}\cdot \underset{0}{\overset{\frac{\pi }{2}}{\int }}\frac{d\theta }{\sqrt{1-\frac{1}{2}{\sin }^2\theta }}=4\cdot \frac{c}{\sqrt{2}}\cdot K\left(\frac{1}{\sqrt{2}}\right)$

де $K\left(k\right)$ — повний еліптичний інтеграл 1-го роду.

• Площа полярного сектора, що відповідає кутам $\phi \in [0,\phi ]$, при $0\le \phi \le \frac{\pi }{4}$: Шаблон:Sfn Шаблон:Rp

  $S(\phi )=\frac{c^2}{2}\cdot \sin (2\phi )$.

Перпендикуляр, проведений із фокуса лемніскати на радіус-вектор будь-якої її точки, ділить площу відповідного сектора навпіл.Шаблон:Sfn Шаблон:Rp

Площа кожної петлі: $2\cdot S\left(\frac{\pi }{4}\right)=c^2$.

Тобто, площа, обмежена всією лемніскатою Бернуллі дорівнює площі квадрата зі стороною $c\sqrt{2}$.Шаблон:Sfn Шаблон:Rp

• • Радіус кривини лемніскати Бернуллі в довільній її точці можна обчислити за формулою:

$R=\frac{2c^2}{3\rho }=\frac{\rho }{3\cos 2\phi }=\frac{N}{3}$.

де $\rho$ — радіус-вектор цієї точки. $N$ — довжина полярної нормалі.

Тобто радіус кривини в довільній точці лемніскати втричі менший за довжину полярної нормалі в цій точці.Шаблон:Sfn Шаблон:Rp Шаблон:Hider

Побудова

Побудова лемніскати з допомогою трьох відрізків. $AC=BD=\sqrt{2}a,CD=2a$

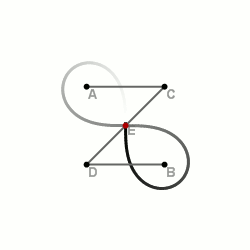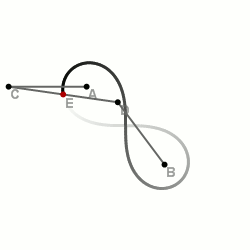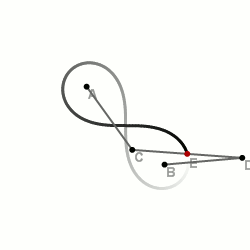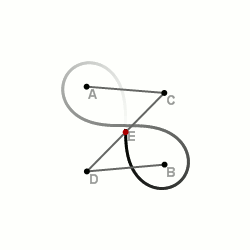
З допомогою трьох відрізків

Це один із найпростіших і найшвидших способів, однак потребує наявності додаткових пристосувань.

На площині вибираються дві точки — $A$ і $B$ — майбутні фокуси лемніскати. Складається спеціальна конструкція із трьох відрізків, скріплених в одну лінію так, щоб отримана лінія могла вільно вигинатися в двох місцях (точки вигину — $C$ та $D$). При цьому необхідно зберігати пропорції відрізків: $AC=BD=\frac{AB}{\sqrt{2}},CD=AB$. Кінці лінії закріплюються до фокусів. При непараллельному повертанні відрізків навколо фокусів середина центрального відрізка описуватиме лемніскату Бернуллі.

За допомогою січних (спосіб Маклорена)

Будується коло радіуса $\frac{c}{\sqrt{2}}$ з центром в одному із фокусів. Із середини $O$ фокусного відрізка будується довільна січна $OPS$ ($P$ i $S$ — точки перетину з колом), і на ній в обидві сторони відкладаються відрізки $O{M}_1$ і $O{M}_2$, рівні хорді $PS$. Точки $M_1$, $M_2$ лежать на різних петлях лемніскати.

Застосування

• Лемніската використовується як перехідна лінія на заокругленнях малого радіуса на залізничних коліях в гірничій місцевості, а також трамвайних коліях.
• Еквіпотегційні лінії поля, яке створюється двома паралельними токами, що протікають вздовж нескінченно довгих провідників, в площині, яка перпендикулярна до них, в окремих випадках є лемніскатами.
• Як довів Бонаті, Лемніската є кривою, що володіє тією властивістю, що матеріальна точка великої ваги, виходячи із стану спокою, під дією сили тяжіння переміщається по дузі лемніскати за той самий час, що і по відповідній хорді. При цьому, центр лемніскати збігається з початковим положенням рухомої точки, а її вісь нахилена щодо вертикалі під кутом 45°.Шаблон:Sfn Шаблон:Rp

Див. також

• Лемніската
• Овал Кассіні
• Синусоїдальна спіраль

Література

• Шаблон:Фіхтенгольц.укр
• Шаблон:Cite book
• Шаблон:Книга

• Шаблон:Книга

• Шаблон:Cite book

• Шаблон:Cite book

Посилання

• Шаблон:MathWorld
• Шаблон:MacTutor
• Robert FERRÉOL, LEMNISCATE OF BERNOULLI на сайті [1], 2017
• Шаблон:Springer *Fagnano e gli archi di lemniscata (Фаньяно та довжина дуги лемніскати) (італ.)