Таблиця сумарних площ

Використання таблиці сумарних площ (2.) магічного квадрата шостого порядку (1.) для підсумовування підпрямокутника його значень; кожна кольорова пляма висвітлює суму всередині прямокутника її кольору.

Табли́ця сума́рних пло́щ (Шаблон:Lang-en) — це структура даних та алгоритм для швидкого й ефективного породжування суми значень у прямокутній підмножині ґратки. В галузі обробки зображень вона також відома як інтегра́льне зобра́ження (Шаблон:Lang-en). Її було запроваджено в комп'ютерній графіці 1984 року Шаблон:Нп для використання з MIP-текстуруванням. У комп'ютернім баченні її популяризував Льюїс, а потім вона отримала назву «інтегрального зображення» та широке використання в системі Віоли — Джонса виявляння об'єктів 2001 року. Історично цей принцип дуже добре відомий у дослідженні багатовимірних функцій розподілу ймовірності, а саме в обчисленні двовимірних (або N-вимірних) імовірностей (площ під розподілом імовірності) з відповідних кумулятивних функцій розподілу.

Алгоритм

Як підказує назва, значення в будь-якій точці (x, y) таблиці сумарних площ — це сума всіх пікселів вище та ліворуч від (x, y), включно:

$I(x,y)=\sum _{\begin{array}{c}{x}^{\prime }\le x\\ y^{\prime }\le y\end{array}}i(x^{\prime },y^{\prime })$

де $i(x,y)$ це значення пікселя в (x, y).

Таблицю сумарних площ можливо ефективно обчислювати за один прохід зображенням, оскільки значення в ній в (x, y) це просто

$I(x,y)=i(x,y)+I(x,y-1)+I(x-1,y)-I(x-1,y-1)$ (Зверніть увагу, що цю сумарну матрицю обчислюють з верхнього лівого кута)

Опис обчислення суми в структурі даних/алгоритмі таблиці сумарних площ

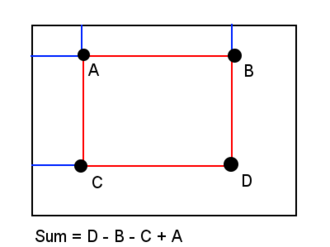
Щойно таблицю сумарних площ було обчислено, для обчислення суми яскравостей будь-якої прямокутної області потрібно рівно чотири посилання на масив незалежно від розміру області. Тобто, за позначень на рисунку праворуч, маючи A=(x₀, y₀), B=(x₁, y₀), C=(x₀, y₁) та D=(x₁, y₁), сума i(x, y) у прямокутнику, охопленому A, B, C та D, дорівнює:

$\sum _{\begin{array}{c}{x}_0<x\le x_1\\ y_0<y\le y_1\end{array}}i(x,y)=I(D)+I(A)-I(B)-I(C)$

Розширення

Цей метод природно розширюється на неперервні області.

Цей метод також можливо розширити на зображення високої вимірності. Якщо кути прямокутника — $x^p$ з $p$ в $\{0,1{\}}^d$, то суму значень зображення, які містяться в цьому прямокутнику, обчислюють за формулою

$\sum _{p\in \{0,1{\}}^d}(-1{)}^{d-\Vert p{\Vert }_1}I(x^p)$

де $I(x)$ — інтегральне зображенням в $x$, а $d$ — вимірність зображення. Запис $x^p$ відповідає у наведеному вище прикладі $d=2$, $A=x^{(0,0)}$, $B=x^{(1,0)}$, $C=x^{(1,1)}$ та $D=x^{(0,1)}$. У нейровізуалізації, наприклад, зображення мають вимірність $d=3$ або $d=4$, при використанні вокселів або вокселів із часовою міткою.

Цей метод було розширено до інтегрального зображення високого порядку, як у праці Фана зі співавт., які запропонували два, три або чотири інтегральні зображення для швидкого та ефективного обчислювання стандартного відхилення (дисперсії), коефіцієнту асиметрії та коефіцієнта ексцесу локального блоку зображення. Це описано докладно нижче:

Для обчислювання дисперсії та стандартного відхилення блоку нам потрібні два інтегральні зображення:

$I(x,y)=\sum _{\begin{array}{c}{x}^{\prime }\le x\\ y^{\prime }\le y\end{array}}i(x^{\prime },y^{\prime })$

$I^2(x,y)=\sum _{\begin{array}{c}{x}^{\prime }\le x\\ y^{\prime }\le y\end{array}}{i}^2(x^{\prime },y^{\prime })$

Дисперсію визначають як

$\mathrm{Var}(X)=\frac{1}{n}\sum _{i=1}^n(x_i-\mu {)}^2.$

Нехай $S_1$ та $S_2$ позначують суми блоку $ABCD$ з $I$ та $I^2$ відповідно. Обчислювати $S_1$ та $S_2$ інтегральними зображеннями швидко. Тепер ми перетворюємо рівняння дисперсії так:

$\mathrm{Var}(X)=\frac{1}{n}\sum _{i=1}^n(x_i^2-2\cdot \mu \cdot x_i+{\mu }^2)=\frac{1}{n}(\sum _{i=1}^n(x_i{)}^2-2\cdot \sum _{i=1}^n(\mu \cdot x_i)+\sum _{i=1}^n({\mu }^2))=\frac{1}{n}(\sum _{i=1}^n(x_i{)}^2-2\cdot \sum _{i=1}^n(\mu \cdot x_i)+n\cdot ({\mu }^2))$

$=\frac{1}{n}(\sum _{i=1}^n(x_i{)}^2-2\cdot \mu \cdot \sum _{i=1}^n(x_i)+n\cdot ({\mu }^2))=\frac{1}{n}(S_2-2\cdot S_1/n\cdot S_1+n\cdot ((S_1/n{)}^2))=\frac{1}{n}(S_2-(S_1{)}^2/n)$

Де $\mu =S_1/n$, а $S_2=\sum _{i=1}^n(x_i^2)$ .

Подібно до оцінювання середнього значення ($\mu$) та дисперсії ($Var$), для яких потрібні інтегральні зображення першого та другого степеня зображення відповідно (тобто $I,I^2$), маніпуляції, подібні до згаданих вище, можливо виконати з третім і четвертим степенями зображень (тобто $I^3(x,y),I^4(x,y)$) для отримання коефіцієнтів асиметрії та ексцесу. Але одна важлива деталь втілення, яку слід мати на увазі для вищевказаних методів, як зазначили Ф. Шафаіт зі співавт., полягає в переповненні цілих чисел, що виникає для інтегральних зображень вищого порядку у випадку використання 32-розрядних цілих чисел.

Див. також

• Шаблон:Нп

Посилання

• Втілення сумарної таблиці у виявлянні об'єктів

Відео лекцій

• Вступ до теорії алгоритму інтегрального зображення Шаблон:Ref-en
• Демонстрація безперервної версії алгоритму інтегрального зображення від Wolfram Demonstrations Project Шаблон:Ref-en