Надлишковий код

Надлишковий код (Шаблон:Lang-en) — в теорії кодування завадостійкий код, здатний відновити цілі пакети даних у разі їх втрати. Такий код дозволяє боротися з витоками даних під час передачі каналами зв'язку або роботі з пам'яттю. Зазвичай він використовується, коли точна позиція втрачених даних відома апріорі.

Графічне представлення процесів кодування та декодування

Принцип роботи

Надлишковий код перетворює повідомлення з $k$ символів у довше повідомлення (кодове слово) з $n$ символів так, що вихідне повідомлення може бути відновлено за $k^{\prime }$ будь-якими символами. Такий код називається $(n,k)$ кодом, вираз $r=k/n$ — кодовою часткою, вираз $k^{\prime }/k$ — ефективністю прийому.

Надлишковий код зазвичай використовується на верхніх рівнях стека протоколів каналів передачі та зберігання інформації.

Оптимальний надлишковий код

Оптимальний надлишковий код відрізняється тим, що будь-яких $k$ з $n$ символів кодового слова достатньо для відновлення вихідного повідомлення, тобто вони мають оптимальну ефективність прийому.

Перевірка парності

Розглянемо випадок, коли $n=k+1$. За допомогою набору з $k$ значень $\{v_i{\}}_{1\le i\le k}$ обчислюється контрольна сума та додається до $k$ вихідних значеннь:

$v_{k+1}=-\sum _{i=1}^k{v}_i$ .

Тепер у набір $\{v_i{\}}_{1\le i\le k+1}$ з $k+1$ значень включено контрольну суму. У разі втрати одного із значень $v_e$, його можна буде з легкістю відновити за допомогою підсумовування:

$v_e=-\sum _{i=1,i\ne e}^{k+1}{v}_i$ .

Більш складні комбінації шуканих і отримуваних значень є Шаблон:Не перекладено.

Лінійний код

Важливим підкласом надлишкового коду є лінійний код. Його назва пов'язана з тим, що він може бути проаналізований за допомогою лінійної алгебри. Нехай $x=x_0\dots x_{k-1}$ — вихідні дані, $G$ — матриця розміру $n\times k$ тоді закодовані дані $(n,k)$ — коди можуть бути представлені як $\overrightarrow{y}=G\overrightarrow{x}$. Припустимо, що приймач отримав $k$ компонент вектора $\overrightarrow{y}$, тоді вихідні дані можуть бути відновлені за допомогою $k$ рівнянь, пов'язаних із відомими компонентами вектора $\overrightarrow{y}$. Нехай матриця $G^{\prime }$ розміру $k\times k$ відповідає цій системі рівнянь. Відновлення можливе, якщо всі ці рівняння лінійно незалежні і в загальному випадку це означає, що будь-яка матриця розміру $k\times k$ оборотна. Матриця $G$ називається генеруючою матрицею коду, тому що будь-який допустимий $\overrightarrow{y}$ може бути отриманий як лінійна комбінація стовпців матриці $G$. Оскільки її ранг дорівнює $k$, то будь-яка підмножина з $k$ закодованих елементів має містити інформацію про всі $k$ вихідних даних. Для отримання вихідних даних необхідно вирішити лінійну систему: $\overrightarrow{y^{\prime }}=G^{\prime }\overrightarrow{x}$, де $\overrightarrow{y^{\prime }}$ — підмножина з $k$ елементів вектора $\overrightarrow{y}$, доступних на приймачі.

Поліноміальна передискретизація

Приклад: Несправна електронна пошта (Шаблон:Lang-en)

У випадку, коли $k=2$ надлишкові символи можуть бути створені як проміжні точки на відрізку, що з'єднує два вихідні символи. Це показано на простому прикладі, який називається несправною електронною поштою:

Аліса порахувала значення $f(1)$ і $f(2)$

Аліса хоче надіслати свій телефонний номер (555629) Бобу, використовуючи несправну електронну пошту. Цей вид пошти працює так само, як звичайна електронна пошта, за таким винятком:

1. Близько половини всіх повідомлень губляться.
2. Повідомлення довші за 5 символів заборонені.
3. Це дуже дорого.

Замість того, щоб запитати у Боба підтвердження повідомлення, яке вона надіслала, Аліса вигадує таку схему:

1. Вона розбиває свій телефонний номер на дві частини $a=555,b=629$ і надсилає 2 повідомлення Бобу — «A = 555» і «B = 629»
2. Вона будує лінійну функцію $f(i)=a+(b-a)(i-1)$, у цьому прикладі $f(i)=555+74(i-1)$. Таким чином $f(1)=555$ і $f(2)=629$.
3. Вона вважає значення $f(3)=703,f(4)=777$ і $f(5)=851$, а потім відправляє три надлишкові повідомлення: «C=703», «D=777» і «E=851».

Боб знає, що вираз для $f(k)$ наступне $f(i)=a+(b-a)(i-1)$, де $a$ і $b$ — дві частини телефонного номера. Тепер припустимо, що Боб отримує «D = 777» і «E = 851».

Боб отримує два повідомлення з $f(4)$ і $f(5)$

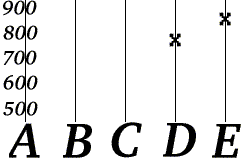
Боб може відновити телефонний номер Аліси за допомогою $a$ і $b$, використовуючи значення $f(4)$ і $f(5)$, які він отримав. Більш того, він може це зробити, використовуючи два будь-які отримані повідомлення. Отже, у цьому прикладі кодова частка дорівнює 40 %. Зауважимо, що Аліса не може закодувати свій номер телефону лише в одному повідомленні такої пошти, оскільки він складається з 6 символів, а максимальна довжина одного повідомлення — 5 символів. Якби вона відправляла свій номер телефону частинами, запитуючи підтвердження кожної частини від Боба, то було б відправлено мінімум 4 повідомлення (два від Аліси і два підтвердження від Боба).

Загальний випадок

Наведена вище лінійна конструкція може бути узагальнена до поліноміальної інтерполяції. У такому разі крапки тепер обчислюються над кінцевим полем ${𝔽}_{2^m}$, де $m$ — число біт у символі. Відправник нумерує символи даних від $0$ до $k-1$ і посилає їх. Потім він будує, наприклад, інтерполяційний многочлен Лагранжа $p(x)$ степеня $k$, так що $p(i)$ дорівнює $i$ -ому символу даних. Потім він відправляє $p(k),\dots ,p(n-1)$. За допомогою поліноміальної інтерполяції одержувач зможе відновити втрачені дані у разі, якщо він успішно прийняв $k$ символів.

Реалізація у реальному світі

Цей процес реалізований у Коді Ріда — Соломона з кодовими словами, сконструйованими над кінцевим полем при використанні визначника Вандермонда.

Майже оптимальний надлишковий код

Майже оптимальний надлишковий код вимагає $(1+\epsilon )k$ символів, щоб відновити повідомлення (де $\epsilon >0$). Величина $\epsilon$ може бути зменшена за рахунок додаткового часу роботи процесора. При використанні таких кодів необхідно вирішити, що краще: складність обчислень або можливість корекції повідомлень. У 2004 році існував тільки один майже оптимальний надлишковий код з лінійним часом кодування та декодування — Шаблон:Не перекладено.

Застосування

Надлишкові коди застосовуються в:

• Шаблон:Не перекладено (наприклад, у групі з надійного мультимовлення IETF)
• 3GPP (MBMS та eMBMS (Шаблон:Не перекладено)
• однорангові мережі, наприклад, для вирішення проблеми передачі останнього блоку даних
• Розподільні сховища.

Приклади

Тут наведено деякі приклади різних кодів.

Майже оптимальні надлишкові коди

• Код із малою щільністю перевірок на парність

Оптимальні надлишкові коди

• Біт парності
• Код Ріда — Соломона

Література

• Шаблон:Книга