Індуктивна границя

Індуктивна (або пряма) границя  — конструкція, що виникла спочатку в теорії множин і топології, а потім знайшла широке застосування в багатьох розділах математики. Двоїсте поняття  — проективна (або обернена) границя.

Ця конструкція дозволяє побудувати новий об'єкт $X$ по послідовності (індексованій направленою множиною) однотипних об'єктів $X_i$ і набору відображень $f_{ij}:X_i\to X_j$, $i⩽j$. Для індуктивної границі зазвичай використовується позначення

$X=\underrightarrow{\lim }{X}_i$.

Ми дамо визначення для алгебраїчних структур, а потім  — для об'єктів довільної категорії.

Визначення

Алгебраїчні об'єкти

У цьому розділі буде дано визначення, що підходить для множин з додатковою структурою, таких як групи, кільця, модулі над фіксованим кільцем.

Нехай $I$  — направлена множина з відношенням передпорядку $⩽$ і нехай кожному елементу $i\in I$ відповідає алгебраїчний об'єкт $X_i$, а кожній парі $(i,j)$, $i,j\in I$, в якій $i⩽j$, відповідає гомоморфізм $f_{ij}:X_i\to X_j$, причому $f_{ii}$  — тотожні відображення для будь-якого $i\in I$ і $f_{ik}=f_{jk}\circ f_{ij}$ для будь-яких $i⩽j⩽k$ з $I$. Таку систему об'єктів і гомоморфізмів називають також направленою системою.

Тоді множина-носій прямої межі направленої системи $(X_i,f_{ij})$  — це фактор-множина диз'юнктного об'єднання множин-носіїв $X_i$ по відношенню еквівалентності:

$\underrightarrow{\lim }{X}_i=\underset{i}{⨆}{X}_i/\sim .$

Тут $x_i\in X_i$ і $x_j\in X_j$ еквівалентні, якщо існує таке $k\in I$, що $f_{ik}(x_i)=f_{jk}(x_j)$. Інтуїтивно, два елементи диз'юнктного об'єднання еквівалентні, тоді і тільки тоді, коли вони «рано чи пізно стануть еквівалентними» в направленій системі. Більш просте формулювання  — це транзитивне замикання відносини еквівалентності «кожен елемент еквівалентний своїм образам», тобто $x_i\sim f_{ik}(x_i)$.

З цього визначення легко отримати канонічні морфізми ${\varphi }_i:X_i\to X$, котрі відправляють кожен елемент в його клас еквівалентності. Алгебраїчну структуру на $X$ можна отримати, виходячи із цих гомоморфізмів.

Визначення для довільної категорії

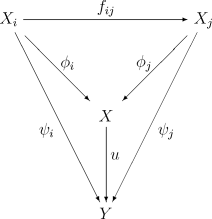
У довільній категорії пряму границю можна визначити за допомогою її універсальної властивості. А саме, пряма границя направленої системи $(X_i,f_{ij})$  — це об'єкт $X$ категорії, такий що виконуються наступні умови:

1. Існують такі відображення ${\varphi }_i:X_i\to X$, що ${\varphi }_i={\varphi }_j\circ f_{ij}$ для будь-яких $i⩽j$;
2. Для будь-яких відображень ${\psi }_i:X_i\to Y$, в довільний обєкт $Y$, для яких виконані рівності ${\psi }_i={\psi }_j\circ f_{ij}$ для будь-яких $i⩽j$, існує єдине відображення $u:X\to Y$, що ${\psi }_i=u\circ {\varphi }_i$, для всіх $i\in I$.

Більш загально, пряма границя направленої системи  — це те ж саме, що її кограниця в сенсі теорії категорій.

Приклади

• На довільній сім'ї підмножин даної множини можна задати структуру передпорядку по включенню. Якщо цей передпорядок дійсно є направленим, то прямою границею є звичайне об'єднання множин.
• Нехай p  — просте число. Розглянемо направлену систему з груп Z/pⁿZ і гомоморфізмів Z/pⁿZ > Z/pⁿ⁺¹Z, індукованих множенням на p. Пряма границя цієї системи містить всі корені з одиниці, порядок яких  — деякий степінь p. Їх група по множенню називається групою Прюфера Z(p^∞).
• Нехай F  — пучок на топологічному просторі X зі значеннями в C. Зафіксуємо точку x в X. Відкриті околи x утворюють направлену систему по включенню (U ≤ V якщо U містить V). Функтор пучка зіставляє їй направлену систему ( F(U), r_U,V ), де r  — відображення обмеження. Пряма границя цієї системи складається з ростків F над x і позначається F_x .
• Прямі межі в категорії топологічних просторів виходять присвоєнням фінальна топологія відповідної множини-носія.

Література

• С. Маклейн. Категории для работающего математика, — Москва: ФИЗМАТЛИТ, 2004. — 352 с. — ISBN 5-9221-0400-4.
• Шаблон:Citation
• Шаблон:Citation
• Шаблон:Citation