Ізотомічне спряження

У планіметрії ізотомічним спряженням називають одне з перетворень площини, що породжується заданим на площині трикутником $ABC$.

Визначення

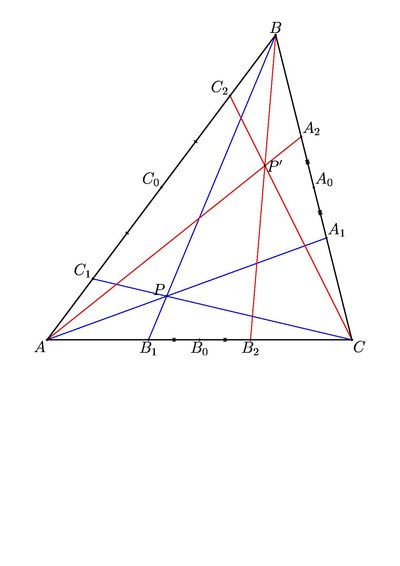
Нехай дано трикутник $ABC$, у якого $A_0$ — середина сторони $BC$, $B_0$ — середина $AC$ і $C_0$ — середина сторони $AB$. Нехай також на площині вибрано довільну точку $P$, яка не лежить на прямих, що містять його сторони. Тоді розглянемо прямі $AP$, $BP$ і $CP$. Нехай вони перетинають прямі, що містять протилежні сторони трикутника, відповідно в точках $A_1$, $B_1$ і $C_1$ (якщо прямі виявляться паралельними, точкою перетину вважається нескінченно віддалена точка прямої). Згідно з теоремою Чеви, $\frac{A{C}_1}{C_{1}B}\cdot \frac{B{A}_1}{A_{1}C}\cdot \frac{C{B}_1}{B_{1}A}=1$. Якщо тепер точки $A_1$, $B_1$ і $C_1$ симетрично відбити відносно $A_0$, $B_0$ і $C_0$ відповідно, вийдуть точки $A_2$, $B_2$ і $C_2$ (нескінченно віддалена точка переходить сама в себе). Оскільки $A{C}_1=B{C}_2$, $A{C}_2=B{C}_1$ і так само для інших пар точок, отримуємо $1=\frac{A{C}_1}{C_{1}B}\cdot \frac{B{A}_1}{A_{1}C}\cdot \frac{C{B}_1}{B_{1}A}=\frac{B{C}_2}{C_{2}A}\cdot \frac{C{A}_2}{A_{2}B}\cdot \frac{A{B}_2}{B_{2}C}$ і, згідно з тією ж теоремою Чеви, прямі $A{A}_2$, $B{B}_2$ і $C{C}_2$ перетинаються в одній точці $P^{\prime }$. Ця точка називається ізотомічно спряженою точці $P$ відносно трикутника $ABC$.

Ізотомічне спряження встановлює взаємно-однозначну відповідність між точками площини з виключеними прямими $AB$, $BC$ і $AC$. На цих прямих відповідність не є взаємно-однозначною, так будь-якій точці прямої $BC$ відповідає вершина $A$ (і навпаки, вершині $A$ — будь-яка точка $BC$) тощо.

Координати

Якщо барицентричні координати точки $P$ дорівнюють $(p:q:r)$, то барицентричні координати ізотомічно спряженої їй точки $P^{\prime }$ дорівнюють $(\frac{1}{p}:\frac{1}{q}:\frac{1}{r})$.

Якщо трилінійні координати точки $P$ дорівнюють $(p:q:r)$, То трилінійні координати ізотомічно спряженої їй точки $P^{\prime }$ дорівнюють $(\frac{1}{a^{2}p}:\frac{1}{b^{2}q}:\frac{1}{c^{2}r})$.

Інше визначення

Якщо замість симетричної чевіани взяти чевіану, основа якої віддалена від середини сторони так само, як і основа початкової, то такі чевіани також перетнуться в одній точці. Отримане перетворення називають ізотомічним спряженням. Воно також переводить прямі в описані коніки. Під час афінних перетворень ізотомічно спряжені точки переходять в ізотомічно спряжені. За ізотомічного спряження в нескінченно віддалену пряму перейде описаний еліпс Штейнера.

Властивості

• Ізотомічне спряження є симетрією, тобто його квадрат тривіальний.
• Нерухомими точками (тобто такими, що переходять самі в себе) ізотомічного спряження є центроїд (інші назви: барицентр або центр мас, тобто точка перетину медіан) трикутника $ABC$ і точки, симетричні вершинам трикутника відносно середин протилежних сторін.
• Точки Жергонна і Наґеля ізотомічно спряжені.
• Точці Лемуана (точці перетину симедіан) трикутника ізотомічно спряжена його точка Брокара.
• Точці перетину бісектрис (інцентру) ізотомічно спряжена точка перетину антибісектрис.
• Прямі загального положення відносно трикутника за ізотомічного спряження переходять в описані навколо нього коніки, і навпаки.

Див. також

• Ізогональне спряження

Посилання

• А. Г. Мякішев «Елементи геометрії трикутника», М., МЦНМО, 2002 Шаблон:Webarchive
• Е. Шаблон:Webarchive А. Шаблон:Webarchive Куланін, А. Шаблон:Webarchive Г. Шаблон:Webarchive Мякішев «Про деякі кониках, пов'язаних з трикутником» Шаблон:Webarchive