Стрічка Мебіуса

Стрі́чка Ме́біуса чи Смужка Мебіуса (німецька вимова Шаблон:IPA]) є поверхнею лише з однією стороною і лише одним краєм. Вона має математичну властивість неорієнтованості. Також вона є лінійчатою поверхнею. Вона була незалежно відкрита німецькими математиками Мебіусом і Лістінгом в 1858 році. Однак відповідні фігури зустрічаються ще у римський мозаїці 200 - 250 років нашої ери^[1]^[2].

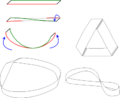
Модель стрічки Мебіуса можна виготовити з довгої прямокутної смужки паперу, закрутивши один з її кінців на півоберту і поєднавши короткі її краї для створення замкненої поверхні.

В евклідовому просторі є два типи стрічок Мебіуса, в залежності від напряму здійсненого півоберту: закручена за годинниковою стрілкою та проти. Звідси можна зробити висновок, що стрічка Мебіуса є хіральною поверхнею.

Як абстрактний топологічний простір, стрічка Мьобіуса може бути вкладена в тривимірний евклідів простір багатьма різними способами: як ліво- або правозакручена поверхня (закручена за- або проти годинникової стрілки), а також вона може бути вкладена з непарною кількістю $n$ обертів ( $n > 1$ ), або з вузловим розташуванням центральної лінії.

Будь-які два вкладення з однаковим вузлом для центральної лінії і однаковою кількістю та напрямком скруток є топологічно еквівалентними. Всі ці вкладення мають лише одну сторону та лише одну граничну криву. Але при вкладенні в інші простори стрічка Мьобіуса може мати дві сторони.

Рівняння

Як поверхня в $ℝ^{3}$ , стрічка Мебіуса задається системою параметричних рівнянь:

x (u, v) = (1 + \frac{v}{2} \cos \frac{u}{2}) \cos u,

y (u, v) = (1 + \frac{v}{2} \cos \frac{u}{2}) \sin u,

z (u, v) = \frac{v}{2} \sin \frac{u}{2},

де $0 ⩽ u < 2 π$ та $- 1 ⩽ v ⩽ 1$ . Ці формули задають стрічку Мебіуса ширини 1, чий центральний круг має радіус 1 та лежить у площині $O x y (z = 0)$ з центром в точці $(0, 0, 0)$ . Параметр $u$ пробігає вздовж стрічки, в той час як $v$ задає відстань від краю.

В циліндричних координатах $(r, θ, z)$ , необмежена версія стрічки Мебіуса може бути представлена рівнянням:

\log r \sin (θ / 2) = z \cos (θ / 2),

де функція логарифма має довільну основу.

Властивості

Поверхня Мьобіуса є найпростішою неорієнтованою поверхнею: якщо асиметричний двовимірний об'єкт один раз повністю пройде вздовж стрічки, він повернеться у вихідне положення у вигляді свого дзеркального відображення. Зокрема, вигнута стрілка, що вказує напрямок за годинниковою стрілкою (↻), пройшовши повністю вздовж стрічки, повернеться як стрілка, що вказує напрямок проти годинникової стрілки (↺). Це означає, що в межах поверхні Мьобіуса неможливо послідовно визначити, що означає рухатися «за годинниковою стрілкою» чи «проти годинникової стрілки».
Будь-яка інша поверхня є неорієнтованою тоді і тільки тоді, коли вона містить поверхню Мьобіуса як підмножину.^[3]
Стрічки Мьобіуса з непарною кількістю напівобертів, більшою за одиницю, або які зав'язані вузлом перед склеюванням, відрізняються як вбудовані підмножини тривимірного простору, хоча всі вони еквівалентні як двовимірні топологічні об'єкти.^[4]

Шаблон:Multiple image

Якщо розрізати стрічку по центральній лінії, то замість двох стрічок Мебіуса утвориться одна довга, двостороння, вдвічі більш закручена стрічка. Ця поверхня є топологічно еквівалентною до циліндра.
Якщо тепер цю двічі скручену стрічку ще раз так само розрізати по центральній лінії, то утворяться дві з'єднані двічі скручені (двосторонні) стрічки, намотані одна на одну.
Якщо стрічку Мьобіуса розрізати вздовж по лінії, що проходить від краю на третину її ширини, то отримаємо дві з'єднані між собою стрічки: одна з них, тонша, буде поверхнею Мьобіуса, а друга буде двічі закрученою двосторонньою поверхнею.^[4]

Стрічка Мебіуса зроблена зі смужки паперу або стрічки.
Щоб перетворити прямокутник в стрічку Мебіуса, з'єднайте ребра, позначені "A" так, щоб напрями стрілок збіглися.
Схема створення стрічки Мебіуса зі смужки паперу