Шестикутна призма

Шестикутна призма — призма з шестикутною основою. У цього многогранника 8 граней, 18 ребер і 12 вершин[1].
До загострювання багато олівців мають форму довгої шестикутної призми[2].
Напівправильний (або однорідний) многогранник
Якщо всі бічні грані однакові, шестикутна призма є напівправильним многогранником, більш загально, однорідним многогранником і четвертою призмою в нескінченній множині призм, утворених прямокутними бічними гранями і двома правильними основами. Призму можна розглядати як зрізаний шестигранний осоедр, поданий символом Шлефлі t{2,6}. З іншого боку, його можна розглядати як прямий добуток правильного шестикутника на відрізок, що подається як {6}×{}. Двоїстим многогранником шестикутної призми є Шаблон:Не перекладено.
Групою симетрії прямої шестикутної призми є D6h з порядком 24, а групою поворотів є D6 з порядком 12.
Об'єм
Як і для більшості призм, об'єм правильної шестигранної призми можна знайти множенням площі основи (з довжиною сторони ) на висоту , що дає формулу[3]:
Симетрія
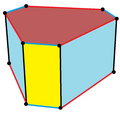
Топологія однорідної шестикутної призми може мати геометричні варіації з низькою симетрією:
| Симетрія | D6h, [2,6], (*622) | C6v, [6], (*66) | D3h, [2,3], (*322) | D3d, [2+,6], (2*3) | |
|---|---|---|---|---|---|
| Конструкція | {6}×{}, Шаблон:ДКД | t{3}×{}, Шаблон:ДКД | Шаблон:ДКД | s2{2,6}, Шаблон:ДКД | |
| Малюнок | 
|

|

|

| |
| Порушення | 
|
|
 
|

| |
Як частина просторових мозаїк
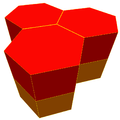
Шестигранна призма присутня як комірка в чотирьох призматичних Шаблон:Не перекладено у тривимірному просторі:
| Шестикутний призматичний стільник[1] Шаблон:ДКД |
Шаблон:Нп Шаблон:ДКД |
Шаблон:Нп Шаблон:ДКД |
Шаблон:Нп Шаблон:ДКД |
|
|

|

|
Шестигранні призми є також тривимірними гранями чотиривимірних Шаблон:Нп:
Пов'язані многогранники і мозаїки
Шаблон:Шестикутні діедричні усічення Цей многогранник можна вважати членом послідовності однорідних многогранників з кутовою фігурою (4.6.2 p) і діаграмою Коксетера — Динкіна Шаблон:ДКД. Для p<6 членами послідовності є усічені у всіх кутах многогранники (зоноедри), і вони показані нижче як сферичні мозаїки. Для p>6 вони є мозаїками гіперболічної площини починаючи зі Шаблон:Нп. Шаблон:Таблиця повністю зрізаних мозаїк
Див. також
Примітки
Посилання
- Uniform Honeycombs in 3-Space Шаблон:Webarchive Моделі у форматі VRML
- The Uniform Polyhedra Шаблон:Webarchive
- Virtual Reality Polyhedra Шаблон:Webarchive The Encyclopedia of Polyhedra
- Prisms and antiprisms Шаблон:Webarchive
- Шаблон:MathWorld
- Hexagonal Prism Interactive Model — Перегляд призм у вебоглядачі