Тестові функції для оптимізації

У прикладній математиці тестові функції для оптимізації (штучні ландшафти) — нелінійні функції, які використовують для оцінки характеристик алгоритмів оптимізації, таких як: швидкість збіжності; точність; грубість; загальні характеристики.

Нижче наведені деякі функції тестування оптимізаційних алгоритмів, що дозволяють отримати уявлення про різні характерні ситуації, з якими стикаються алгоритми оптимізації при вирішенні задач такого роду. У першій частині наведені функції для тестування алгоритмів пошуку глобального мінімуму (максимуму). У другій частині функції з відповідними фронтами для алгоритмів багатокритеріальної оптимізації.

Штучні ландшафти, наведені для тестування оптимізаційних алгоритмів, взяті з декількох джерел (див. Посилання).

Загальний вигляд рівняння, графік цільової функції, межі змінних об'єкта і координати глобального мінімуму наведені в таблиці.

Функції для алгоритмів пошуку глобального мінімуму

Назва / Рисунок	Формула	Мінімум	Область пошуку
Ackley's function	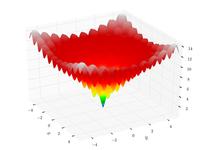$f(x,y)=-20\exp (-0.2\sqrt{0.5(x^2+y^2)})$ $-\exp (0.5(\cos \left(2\pi x\right)+\cos \left(2\pi y\right)))+e+20$	$f(0,0)=0$	$-5\le x,y\le 5$
Sphere function	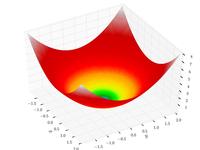$f(𝒙)=\sum _{i=1}^n{x}_i^2$	$f(0,\dots ,0)=0$	$-\mathrm{\infty }\le x_i\le \mathrm{\infty }$, $1\le i\le n$
Функція Розенброка	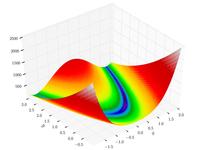$f(𝒙)=\sum _{i=1}^{n-1}[100{(x_{i+1}-x_i^2)}^2+{(x_i-1)}^2]$	$\text{Min}=\{\begin{array}{cc}n=2& \to f(1,1)=0,\\ n=3& \to f(1,1,1)=0,\\ n>3& \to f\left(\underset{(n)\text{ times}}{\underbrace{1,\dots ,1}}\right)=0\end{array}$	$-\mathrm{\infty }\le x_i\le \mathrm{\infty }$, $1\le i\le n$
Beale's function	$f(x,y)={(1.5-x+xy)}^2+{(2.25-x+x{y}^2)}^2$ $+{(2.625-x+x{y}^3)}^2$	$f(3,0.5)=0$	$-4.5\le x,y\le 4.5$
Goldstein–Price function	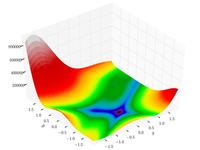$f(x,y)=$ $(1+{(x+y+1)}^2(19-14x+3x^2-14y+6xy+3y^2))$ $(30+{(2x-3y)}^2(18-32x+12x^2+48y-36xy+27y^2))$	$f(0,-1)=3$	$-2\le x,y\le 2$
Booth's function	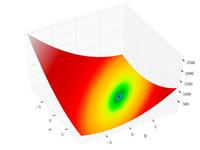$f(x,y)={(x+2y-7)}^2+{(2x+y-5)}^2$	$f(1,3)=0$	$-10\le x,y\le 10$
Bukin function N.6	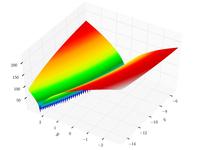$f(x,y)=100\sqrt{|y-0.01x^2|}+0.01|x+10|.$	$f(-10,1)=0$	$-15\le x\le -5$, $-3\le y\le 3$
Matyas function	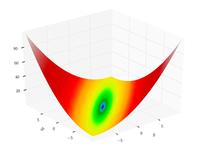$f(x,y)=0.26(x^2+y^2)-0.48xy$	$f(0,0)=0$	$-10\le x,y\le 10$
Lévi function N.13	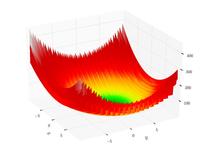$f(x,y)={\sin }^2\left(3\pi x\right)+{(x-1)}^2(1+{\sin }^2\left(3\pi y\right))$ $+{(y-1)}^2(1+{\sin }^2\left(2\pi y\right))$	$f(1,1)=0$	$-10\le x,y\le 10$
Three-hump camel function	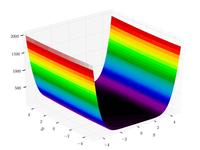$f(x,y)=2x^2-1.05x^4+\frac{x^6}{6}+xy+y^2$	$f(0,0)=0$	$-5\le x,y\le 5$
Easom function	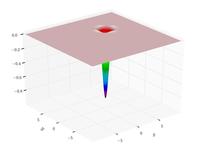$f(x,y)=-\cos \left(x\right)\cos \left(y\right)$ $\exp (-({(x-\pi )}^2+{(y-\pi )}^2))$	$f(\pi ,\pi )=-1$	$-100\le x,y\le 100$
Cross-in-tray function	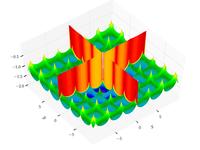$f(x,y)=-0.0001$ ${(|\sin \left(x\right)\sin \left(y\right)\exp \left(|100-\frac{\sqrt{x^2+y^2}}{\pi }|\right)|+1)}^{0.1}$	$\text{Min}=\{\begin{array}{cc}f(1.34941,-1.34941)& =-2.06261\\ f(1.34941,1.34941)& =-2.06261\\ f(-1.34941,1.34941)& =-2.06261\\ f(-1.34941,-1.34941)& =-2.06261\end{array}$	$-10\le x,y\le 10$
Eggholder function	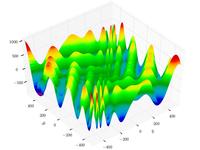$f(x,y)=-(y+47)\sin \left(\sqrt{|\frac{x}{2}+(y+47)|}\right)$ $-x\sin \left(\sqrt{|x-(y+47)|}\right)$	$f(512,404.2319)=-959.6407$	$-512\le x,y\le 512$
Hölder table function	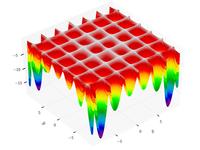$f(x,y)=-|\sin \left(x\right)\cos \left(y\right)\exp \left(|1-\frac{\sqrt{x^2+y^2}}{\pi }|\right)|$	$\text{Min}=\{\begin{array}{cc}f(8.05502,9.66459)& =-19.2085\\ f(-8.05502,9.66459)& =-19.2085\\ f(8.05502,-9.66459)& =-19.2085\\ f(-8.05502,-9.66459)& =-19.2085\end{array}$	$-10\le x,y\le 10$
McCormick function	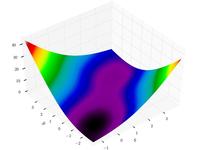$f(x,y)=\sin (x+y)+{(x-y)}^2-1.5x+2.5y+1$	$f(-0.54719,-1.54719)=-1.9133$	$-1.5\le x\le 4$, $-3\le y\le 4$
Schaffer function N. 2	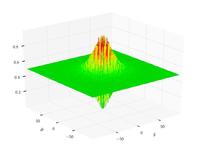$f(x,y)=0.5+\frac{{\sin }^2(x^2-y^2)-0.5}{{(1+0.001(x^2+y^2))}^2}$	$f(0,0)=0$	$-100\le x,y\le 100$
Schaffer function N. 4	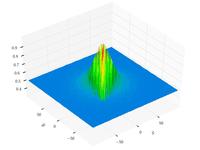$f(x,y)=0.5+\frac{{\cos }^2(\sin \left(|x^2-y^2|\right))-0.5}{{(1+0.001(x^2+y^2))}^2}$	$f(0,1.25313)=0.292579$	$-100\le x,y\le 100$
Styblinski–Tang function	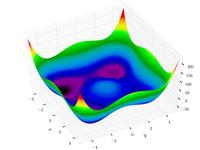$f(𝒙)=\frac{\sum _{i=1}^n{x}_i^4-16x_i^2+5x_i}{2}$	$X=\underset{(n)\text{ times}}{\underbrace{-2.903534,\dots ,-2.903534}}$ $-39.16617n<f(X)<-39.16616n$	$-5\le x_i\le 5$, $1\le i\le n$.
Simionescu function	$f(x,y)=0.1xy$, $\text{subjected to: }{x}^2+y^2\le {(r_T+r_S\cos (n\arctan \frac{x}{y}))}^2$ $\text{where: }{r}_T=1,r_S=0.2\text{ and }n=8$	$f(\pm 0.85586214,\mp 0.85586214)=-0.072625$	$-1.25\le x,y\le 1.25$

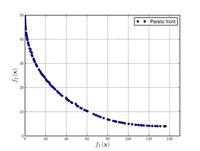
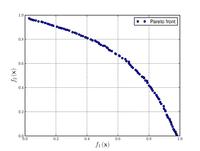
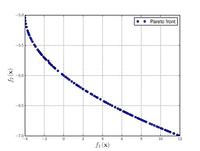
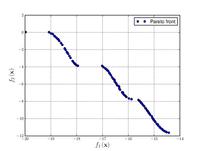
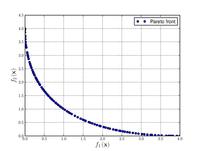
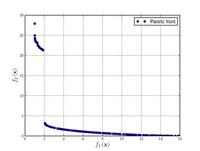
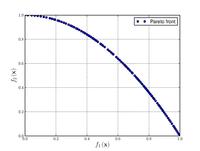
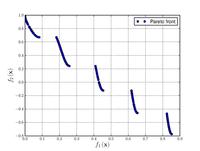
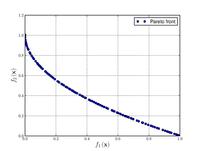
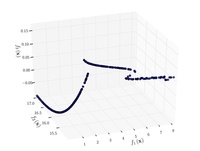
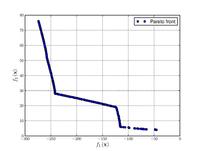
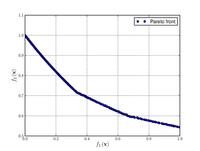
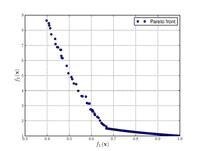
Функції для алгоритмів багатокритеріальної оптимізації

Назва / Рисунок	Формула	Мінімум	Область пошуку
Binh and Korn function	$\text{Minimize}=\{\begin{array}{cc}{f}_1(x,y)& =4x^2+4y^2\\ f_2(x,y)& ={(x-5)}^2+{(y-5)}^2\end{array}$	$\text{s.t.}=\{\begin{array}{cc}{g}_1(x,y)& ={(x-5)}^2+y^2\le 25\\ g_2(x,y)& ={(x-8)}^2+{(y+3)}^2\ge 7.7\end{array}$	$0\le x\le 5$, $0\le y\le 3$
Chakong and Haimes function	$\text{Minimize}=\{\begin{array}{cc}{f}_1(x,y)& =2+{(x-2)}^2+{(y-1)}^2\\ f_2(x,y)& =9x-{(y-1)}^2\end{array}$	$\text{s.t.}=\{\begin{array}{cc}{g}_1(x,y)& =x^2+y^2\le 225\\ g_2(x,y)& =x-3y+10\le 0\end{array}$	$-20\le x,y\le 20$
Fonseca and Fleming function	$\text{Minimize}=\{\begin{array}{cc}{f}_1\left(𝒙\right)& =1-\exp (-\sum _{i=1}^n{(x_i-\frac{1}{\sqrt{n}})}^2)\\ f_2\left(𝒙\right)& =1-\exp (-\sum _{i=1}^n{(x_i+\frac{1}{\sqrt{n}})}^2)\end{array}$		$-4\le x_i\le 4$, $1\le i\le n$
Test function 4	$\text{Minimize}=\{\begin{array}{cc}{f}_1(x,y)& =x^2-y\\ f_2(x,y)& =-0.5x-y-1\end{array}$	$\text{s.t.}=\{\begin{array}{cc}{g}_1(x,y)& =6.5-\frac{x}{6}-y\ge 0\\ g_2(x,y)& =7.5-0.5x-y\ge 0\\ g_3(x,y)& =30-5x-y\ge 0\end{array}$	$-7\le x,y\le 4$
Kursawe function	$\text{Minimize}=\{\begin{array}{cc}{f}_1\left(𝒙\right)& =\sum _{i=1}^2[-10\exp (-0.2\sqrt{x_i^2+x_{i+1}^2})]\\ & \\ f_2\left(𝒙\right)& =\sum _{i=1}^3[{\left|x_i\right|}^{0.8}+5\sin \left(x_i^3\right)]\end{array}$		$-5\le x_i\le 5$, $1\le i\le 3$.
Schaffer function N. 1	$\text{Minimize}=\{\begin{array}{cc}{f}_1\left(x\right)& =x^2\\ f_2\left(x\right)& ={(x-2)}^2\end{array}$		$-A\le x\le A$. Values of $A$ form $10$ to $10^5$ have been used successfully. Higher values of $A$ increase the difficulty of the problem.
Schaffer function N. 2	$\text{Minimize}=\{\begin{array}{cc}{f}_1\left(x\right)& =\{\begin{array}{cc}-x,& \text{if }x\le 1\\ x-2,& \text{if }1<x\le 3\\ 4-x,& \text{if }3<x\le 4\\ x-4,& \text{if }x>4\end{array}\\ f_2\left(x\right)& ={(x-5)}^2\end{array}$		$-5\le x\le 10$.
Poloni's two objective function	$\text{Minimize}=\{\begin{array}{cc}{f}_1(x,y)& =[1+{(A_1-B_1(x,y))}^2+{(A_2-B_2(x,y))}^2]\\ f_2(x,y)& ={(x+3)}^2+{(y+1)}^2\end{array}$ $\text{where}=\{\begin{array}{cc}{A}_1& =0.5\sin \left(1\right)-2\cos \left(1\right)+\sin \left(2\right)-1.5\cos \left(2\right)\\ A_2& =1.5\sin \left(1\right)-\cos \left(1\right)+2\sin \left(2\right)-0.5\cos \left(2\right)\\ B_1(x,y)& =0.5\sin \left(x\right)-2\cos \left(x\right)+\sin \left(y\right)-1.5\cos \left(y\right)\\ B_2(x,y)& =1.5\sin \left(x\right)-\cos \left(x\right)+2\sin \left(y\right)-0.5\cos \left(y\right)\end{array}$		$-\pi \le x,y\le \pi$
Zitzler–Deb–Thiele's function N. 1	$\text{Minimize}=\{\begin{array}{cc}{f}_1\left(𝒙\right)& =x_1\\ f_2\left(𝒙\right)& =g\left(𝒙\right)h(f_1\left(𝒙\right),g\left(𝒙\right))\\ g\left(𝒙\right)& =1+\frac{9}{29}\sum _{i=2}^{30}{x}_i\\ h(f_1\left(𝒙\right),g\left(𝒙\right))& =1-\sqrt{\frac{f_1\left(𝒙\right)}{g\left(𝒙\right)}}\end{array}$		$0\le x_i\le 1$, $1\le i\le 30$.
Zitzler–Deb–Thiele's function N. 2	$\text{Minimize}=\{\begin{array}{cc}{f}_1\left(𝒙\right)& =x_1\\ f_2\left(𝒙\right)& =g\left(𝒙\right)h(f_1\left(𝒙\right),g\left(𝒙\right))\\ g\left(𝒙\right)& =1+\frac{9}{29}\sum _{i=2}^{30}{x}_i\\ h(f_1\left(𝒙\right),g\left(𝒙\right))& =1-{\left(\frac{f_1\left(𝒙\right)}{g\left(𝒙\right)}\right)}^2\end{array}$		$0\le x_i\le 1$, $1\le i\le 30$.
Zitzler–Deb–Thiele's function N. 3	$\text{Minimize}=\{\begin{array}{cc}{f}_1\left(𝒙\right)& =x_1\\ f_2\left(𝒙\right)& =g\left(𝒙\right)h(f_1\left(𝒙\right),g\left(𝒙\right))\\ g\left(𝒙\right)& =1+\frac{9}{29}\sum _{i=2}^{30}{x}_i\\ h(f_1\left(𝒙\right),g\left(𝒙\right))& =1-\sqrt{\frac{f_1\left(𝒙\right)}{g\left(𝒙\right)}}-\left(\frac{f_1\left(𝒙\right)}{g\left(𝒙\right)}\right)\sin \left(10\pi f_1\left(𝒙\right)\right)\end{array}$		$0\le x_i\le 1$, $1\le i\le 30$.
Zitzler–Deb–Thiele's function N. 4	$\text{Minimize}=\{\begin{array}{cc}{f}_1\left(𝒙\right)& =x_1\\ f_2\left(𝒙\right)& =g\left(𝒙\right)h(f_1\left(𝒙\right),g\left(𝒙\right))\\ g\left(𝒙\right)& =91+\sum _{i=2}^{10}(x_i^2-10\cos \left(4\pi x_i\right))\\ h(f_1\left(𝒙\right),g\left(𝒙\right))& =1-\sqrt{\frac{f_1\left(𝒙\right)}{g\left(𝒙\right)}}\end{array}$		$0\le x_1\le 1$, $-5\le x_i\le 5$, $2\le i\le 10$
Zitzler–Deb–Thiele's function N. 6	$\text{Minimize}=\{\begin{array}{cc}{f}_1\left(𝒙\right)& =1-\exp (-4x_1){\sin }^6\left(6\pi x_1\right)\\ f_2\left(𝒙\right)& =g\left(𝒙\right)h(f_1\left(𝒙\right),g\left(𝒙\right))\\ g\left(𝒙\right)& =1+9{\left[\frac{\sum _{i=2}^{10}{x}_i}{9}\right]}^{0.25}\\ h(f_1\left(𝒙\right),g\left(𝒙\right))& =1-{\left(\frac{f_1\left(𝒙\right)}{g\left(𝒙\right)}\right)}^2\end{array}$		$0\le x_i\le 1$, $1\le i\le 10$.
Viennet function	$\text{Minimize}=\{\begin{array}{cc}{f}_1(x,y)& =0.5(x^2+y^2)+\sin (x^2+y^2)\\ f_2(x,y)& =\frac{{(3x-2y+4)}^2}{8}+\frac{{(x-y+1)}^2}{27}+15\\ f_3(x,y)& =\frac{1}{x^2+y^2+1}-1.1\exp (-(x^2+y^2))\end{array}$		$-3\le x,y\le 3$.
Osyczka and Kundu function	$F_1(x)=-25{(x_1-2)}^2-{(x_2-2)}^2$ $-{(x_3-1)}^2-{(x_4-4)}^2-{(x_5-1)}^2$ $\text{Minimize}=\{\begin{array}{cc}{f}_1\left(𝒙\right)& =F_1(x)\\ f_2\left(𝒙\right)& =\sum _{i=1}^6{x}_i^2\end{array}$	$\text{s.t.}=\{\begin{array}{cc}{g}_1\left(𝒙\right)& =x_1+x_2-2\ge 0\\ g_2\left(𝒙\right)& =6-x_1-x_2\ge 0\\ g_3\left(𝒙\right)& =2-x_2+x_1\ge 0\\ g_4\left(𝒙\right)& =2-x_1+3x_2\ge 0\\ g_5\left(𝒙\right)& =4-{(x_3-3)}^2-x_4\ge 0\\ g_6\left(𝒙\right)& ={(x_5-3)}^2+x_6-4\ge 0\end{array}$	$0\le x_1,x_2,x_6\le 10$, $1\le x_3,x_5\le 5$, $0\le x_4\le 6$.
CTP1 function (2 variables)	$\text{Minimize}=\{\begin{array}{cc}{f}_1(x,y)& =x\\ f_2(x,y)& =(1+y)\exp (-\frac{x}{1+y})\end{array}$	$\text{s.t.}=\{\begin{array}{cc}{g}_1(x,y)& =\frac{f_2(x,y)}{0.858\exp (-0.541f_1(x,y))}\ge 1\\ g_1(x,y)& =\frac{f_2(x,y)}{0.728\exp (-0.295f_1(x,y))}\ge 1\end{array}$	$0\le x,y\le 1$.
Constr-Ex problem	$\text{Minimize}=\{\begin{array}{cc}{f}_1(x,y)& =x\\ f_2(x,y)& =\frac{1+y}{x}\end{array}$	$\text{s.t.}=\{\begin{array}{cc}{g}_1(x,y)& =y+9x\ge 6\\ g_1(x,y)& =-y+9x\ge 1\end{array}$	$0.1\le x\le 1$, $0\le y\le 5$

Посилання

• Optimization Test Problems Шаблон:Ref-en
• 3D Function Grapher Шаблон:Ref-en

Джерела

• Bäck, Thomas. Evolutionary algorithms in theory and practice: evolution strategies, evolutionary programming, genetic algorithms. Oxford: Oxford University Press. — 1995. p. 328. ISBN 0-19-509971-0.
• Deb, Kalyanmoy (2002) Multiobjective optimization using evolutionary algorithms (Repr. ed.). Chichester [u.a.]: Wiley. ISBN 0-471-87339-X.
• Binh T. and Korn U. MOBES: A Multiobjective Evolution Strategy for Constrained Optimization Problems. In: Proceedings of the Third International Conference on Genetic Algorithms. Czech Republic. — 1997. pp. 176—182
• Binh T. A multiobjective evolutionary algorithm. The study cases. Technical report. Institute for Automation and Communication. Barleben, Germany. — 1999.