Ознака стиснення Коші

Шаблон:Числення Ознака стиснення Коші — названа на честь Огюстена-Луї Коші, є однією з ознак збіжності для нескінченних рядів.

Для незростаючої послідовності $f(n)$ невід'ємних дійсних чисел, ряд $\sum _{n=1}^{\mathrm{\infty }}f(n)$ збігається тоді й лише тоді, коли «ущільнений» ряд $\sum _{n=0}^{\mathrm{\infty }}{2}^{n}f(2^n)$ збігається. Крім того, якщо вони збігаються, то суми обмежені співвідношенням:

$\sum _{n=1}^{\mathrm{\infty }}f(n)\le \sum _{n=0}^{\mathrm{\infty }}{2}^{n}f(2^n)\le 2\sum _{n=1}^{\mathrm{\infty }}f(n),$

Доведення

Погрупуємо доданки в групи з довжиною рівною степеню двійки (1, 2, 4, …):

$\begin{array}{ccccccccc}\sum _{n=1}^{\mathrm{\infty }}f(n)& =& f(1)& +& (f(2)+f(3))& +& (f(4)+f(5)+f(6)+f(7))& +& \cdots \\ & \le & f(1)& +& (f(2)+f(2))& +& (f(4)+f(4)+f(4)+f(4))& +& \cdots \\ & =& f(1)& +& 2f(2)& +& 4f(4)& +& \cdots =\sum _{n=0}^{\mathrm{\infty }}{2}^{n}f(2^n)\end{array}$

Погрупуємо доданки результату в групи з довжиною рівною степеню двійки по іншому (2, 4, 8, …):

$\begin{array}{cc}\sum _{n=0}^{\mathrm{\infty }}{2}^{n}f(2^n)& =f(1)+(f(2)+f(2))+(f(4)+f(4)+f(4)+f(4))+\cdots \\ & =(f(1)+f(2))+(f(2)+f(4)+f(4)+f(4))+\cdots \\ & \le (f(1)+f(1))+(f(2)+f(2))+(f(3)+f(3))+\cdots =2\sum _{n=1}^{\mathrm{\infty }}f(n)\end{array}$

Візуалізація подвійної нерівності. Шаблон:Li рядів $\sum f(n),\sum 2^{n}f(2^n),2\sum f(n)$ Показані накладеними одна на одну.

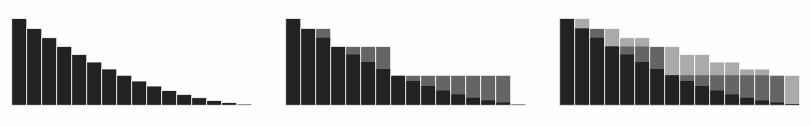
Порівняння інтегралів

Заміна $f(n)\to 2^{n}f(2^n)$ нагадує заміну змінної інтегрування $x\to e^x$, що дає $f(x)\mathrm{d}x\to e^{x}f(e^x)\mathrm{d}x$.

По аналогії з інтегральною ознакою Маклорена — Коші, для монотонної функції $f$: $\sum _{n=1}^{\mathrm{\infty }}f(n)$ збігається тоді і лише тоді, якщо $\underset{1}{\overset{\mathrm{\infty }}{\int }}f(x)\mathrm{d}x$ збігається.

Підстановка $x\to 2^x$ дає інтеграл $\log 2\underset{2}{\overset{\mathrm{\infty }}{\int }}{2}^{x}f(2^x)\mathrm{d}x$. Оскільки $\log 2\underset{2}{\overset{\mathrm{\infty }}{\int }}{2}^{x}f(2^x)\mathrm{d}x<\log 2\underset{0}{\overset{\mathrm{\infty }}{\int }}{2}^{x}f(2^x)\mathrm{d}x$, де права сторона відповідає застосуванню інтегральної ознаки до $\sum _{n=0}^{\mathrm{\infty }}{2}^{n}f(2^n)$. Тому, $\sum _{n=1}^{\mathrm{\infty }}f(n)$ збігається тоді і лише тоді, коли $\sum _{n=0}^{\mathrm{\infty }}{2}^{n}f(2^n)$ збігається.

Приклади

Тест може бути корисним при наявності Шаблон:Mvar у знаменнику Шаблон:Math.

• Найпростіший приклад: гармонійний ряд ${\sum }_{n=1}^{\mathrm{\infty }}1/n$ перетворюється в ряд :$\sum 1$, який явно розбіжний.

• У прикладі

$f(n):=n^{-a}(\log n{)}^{-b}(\log \log n{)}^{-c}.$

Ряд є розбіжним для Шаблон:Math і збіжним для Шаблон:Math. Для Шаблон:Math, перетворення стиснення дає ряд

$\sum n^{-b}(\log n{)}^{-c}.$

Тому за аналогією: ряд є розбіжним для Шаблон:Math, і збіжним для Шаблон:Math. При Шаблон:Math аналогічно працює значення Шаблон:Mvar.

• Аналогічним є алгоритм визначення збіжності для узагальненого ряду Бертрана

$\sum _{n\ge N}\frac{1}{n\cdot \log n\cdot \log \log n\cdots {\log }^{\circ (k-1)}n\cdot ({\log }^{\circ k}n{)}^{\alpha }}(N=\lfloor {\exp }^{\circ k}(0)\rfloor +1)$.

Де $f^{\circ m}$ означає Шаблон:Math-та ітерація функції $f$, тобто: :$f^{\circ m}(x):=\{\begin{array}{cc}f(f^{\circ (m-1)}(x)),& m=1,2,3,\dots ;\\ x,& m=0.\end{array}$

Узагальнення Шльомільха

...

Джерела

• Bonar, Khoury (2006). Real Infinite Series. Mathematical Association of America. Шаблон:ISBN.
• Cauchy condensation test proof